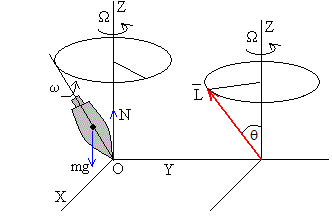
El giróscopo es una rueda giratoria cuyo eje puede cambiar de dirección, tal como se muestra en la figura.

Cuando un sólido en rotación está girando alrededor de un eje principal de inercia $\overrightarrow{L}=I\overrightarrow{\omega }$

En ausencia de momento de fuerzas sobre el sólido, $\overrightarrow{M}$ , el cuerpo seguirá rotando con respecto a dicho eje con velocidad angular constante.

${\displaystyle \overrightarrow{M}=\frac{d\overrightarrow{L}}{dt}}$

Las fuerzas aplicadas sobre el sólido en rotación son:

• El peso mg que actúa sobre el centro de masas, situado a una distancia b del punto de apoyo O.
• La reacción N en el punto de apoyo O

El momento M de las fuerzas respecto del punto fijo O es

mgb·sinφ

El momento angular $\overrightarrow{L}$ cambia de dirección pero no de módulo. El cambio de momento angular $\overrightarrow{\mathrm{dL}}$ tiene la dirección del momento $\overrightarrow{M}$ de las fuerzas aplicadas respecto del punto de apoyo O, ya que el momento $\overrightarrow{M}$ es perpendicular al momento angular $\overrightarrow{L}$, el cambio de momento angular $\overrightarrow{\mathrm{dL}}$ es también perpendicular a $\overrightarrow{L}$.

El extremo del vector momento angular $\overrightarrow{L}$ describe una circunferencia de radio Lsinφ y en un intervalo de tiempo dt se desplaza un ángulo dø. El cambio de momento angular es dL=Lsinφ·dø, de modo que,

${\displaystyle I\omega ·\sin \phi \frac{d\varphi }{dt}=mgb\sin \phi }$

Se denomina velocidad angular de precesión Ω a

${\displaystyle \Omega =\frac{d\varphi }{dt}=\frac{mgb}{I\omega }}$

Cuando el punto de apoyo O coincide con el centro de masas b=0, el momento $\overrightarrow{M}$ de las fuerzas es cero y la velocidad angular de precesión Ω es nula. El eje del giróscopo se mantiene fijo en el espacio.

Los fenómenos giroscópicos tiene muchas aplicaciones: la tendencia de un giróscopo a mantener el eje de rotación fijo en el espacio en ausencia de momento es utilizado en la estabilización de los barcos y en los pilotos automáticos de los aviones.

Otro ejemplo interesante es la precesión de los equinoccios. El plano del ecuador hace un ángulo de 23º 37’ con el plano de la órbita terrestre o eclíptica. La intersección de los dos planos es la línea de los equinoccios. La Tierra es un giróscopo gigante cuyo eje de rotación precesa alrededor del eje perpendicular al plano de la eclíptica con un periodo de 27725 años. La precesión de los equinoccios se debe al momento de las fuerzas ejercido por el Sol y la Luna sobre la Tierra.

Referencias

Alonso M., Finn E. J. Física. Mecánica (1970). Págs. 314-319.