El problema de Kepler
Como hemos deducido en la página, la ecuación de la trayectoria en coordenadas polares es
Por ser la fuerza de atracción una fuerza central, el momento angular L es constante, y por ser conservativa la energía E es constante. El momento angular en coordenadas polares se escribe
Integrando, obtenemos la expresión de la posición angular θ en función del tiempo t.
Vamos a calcular esta integral para las trayectorias elípticas, parabólicas e hiperbólicas
Trayectorias elípticas
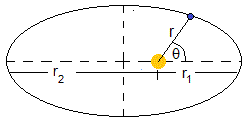
Supongamos un planeta, como la Tierra que se mueve en una órbita elíptica de semieje mayor a y de excentricidad ε=c/a con el Sol situado en el foco F. Sea el periodo, o tiempo que tarda en dar una vuelta completa, P. Al cabo de un cierto tiempo t, el planeta se encuentra en una posición (r, θ). El ángulo θ se denomina anomalía verdadera en el instante t.
Tomamos el tiempo t=0, cuando el planeta pasa por la posición más cercana al centro de fuerzas (perihelio o perigeo), θ=0.
Calculamos la integral haciendo el cambio de variable
con a=(1-ε)/(1+ε), no confundir esta constante con el semieje mayor
La primera integral es inmediata
La segunda integral es algo más laboriosa
Haciendo el cambio, u=tanv, du=dv/cos2(v)
Deshaciendo los cambios
Se ha tenido en cuenta la relación trigonométrica entre sin(2u) y tan(u)
El resultado de la suma de las dos integrales es
Definimos el ángulo E tal que
y teniendo en cuenta la relación trigonométrica entre sin(E) y tan(E/2), la integral queda simplificada
La ecuación de Kepler se escribe
Donde el ángulo E se ha definido como
El periodo P es el tiempo que tarda en dar una vuelta completa un planeta, que describe una órbita elíptica
La forma más simplificada de la ecuación de Kepler para las trayectorias elípticas, es
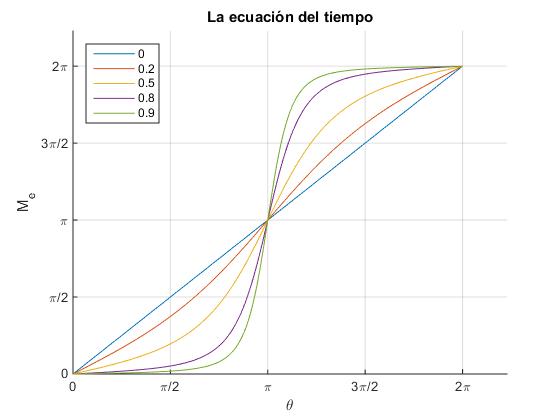
El miembro izquierdo se denota como Me (anomalía media)
Representamos Me en función de la posición angular θ, para los siguientes valores de la excentricidad ε=0, 0.2, 0.5 0.8 y 0.9
x=(0:360)*pi/180;
hold on
for e=[0,0.2,0.5,0.8,0.9]
y=2*atan(sqrt((1-e)/(1+e))*tan(x/2))-e*sqrt(1-e^2)*sin(x).
/(1+e*cos(x));
yy=y.*(y>0)+(2*pi+y).*(y<0);
plot(x,yy, 'displayName',num2str(e))
end
legend('-DynamicLegend','Location','northwest')
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
set(gca,'YTick',0:pi/2:2*pi)
set(gca,'YTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
hold off
grid on
xlabel('\theta')
ylabel('M_e')
title('La ecuación del tiempo')
Ecuación de la trayectoria en términos del ángulo E
La distancia más cercana al Sol r1 se obtiene en la ecuación de la trayectoria con θ=0 , y la más alejada r2 con θ=π. Con r1+r2=2a. Siendo a el semieje mayor de la elipse
con la excentricidad ε<1. La ecuación de la trayectoria en términos del ángulo θ es
Conociendo la relación entre los ángulos θ y E
Determinaremos la ecuación de la trayectoria en términos del ángulo E, utilizando las relaciones trigonométricas
El resultado es
Hemos utilizado las relaciones trigonométricas
Finalmente, la ecuación de la trayectoria es
Dada la posición angular θ del satélite determinar el tiempo t
Teniendo en cuenta las relaciones trigonométricas
Dada la posición angular θ, determinamos el ángulo E mediante las relaciones
Dependiendo del signo del seno y del coseno, se determina el cuadrante y se calcula el ángulo E. Sustituyendo en la ecuación de Kepler, obtenemos Me
Conocido Me, obtenemos el tiempo
Ejemplo
Un satélite artificial describe una órbita elíptica con cuyas distancias máxima y mínima al centro de la Tierra son, respectivamente r1=9.6·106 m y r2=21·106. Determinar el instante t en el que la posición del satélite es θ=2π/3 (120°)
Elaboramos un script para realizar los cálculos
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
r1=9.6e6; %distancia mínima
r2=21e6; %distancia máxima
a=(r1+r2)/2; %semieje mayor
c=a-r1; %semidistancia focal
ex=c/a; %excentricidad
th=2*pi/3; %posición
c_E=(ex+cos(th))/(1+ex*cos(th));
s_E=sqrt(1-ex^2)*sin(th)/(1+ex*cos(th));
E=atan2(s_E,c_E);
if E<0
E=2*pi+E;
end
t=(E-ex*s_E)*a^(3/2)/sqrt(G*M);
disp(t)
4.0757e+03
El instante en el que se alcanza la posición angular θ=2π/3 es t=4076 s
Dado el tiempo t determinar la posición angular θ del satélite
Sustituyendo Me en la ecuación de Kepler, obtenemos una ecuación trascendente cuya raíz tenemos que determinar por procedimientos numéricos
Un procedimiento apropiado para resolver esta ecuación trascendente es el método de Newton. Sea f(x)=0. El proceso iterativo para calcular la raíz es
Se repite el proceso iterativo hasta que se encuentra la raíz E con el nivel de precisión deseado. Una vez determinado E se calcula la posición angular θ mediante la relación
Ejemplo
Encontrar posición angular θ del satélite del ejercicio anterior en el instante t=10800 s (3 horas)
Resolvemos la ecuación trascendente E-ε·sinE=Me por el procedimiento de Newton tomando como valor inicial de partida E0=Me-ε/2=3.418
x0=3.418;
e=0.3725;
Me=3.604;
while(1)
x=x0-(x0-e*sin(x0)-Me)/(1-e*cos(x0));
if abs((x-x0)/x0)<1e-6
break;
end
x0=x;
end
fprintf('La raíz buscada es %1.3f\n',x0)
La raíz buscada es 3.480
Si E=3.480, a partir de la relación
obtenemos la posición angular θ=3.372 del satélite en el instante t=10800 s (3 horas)
Interpretación geométrica del ángulo E
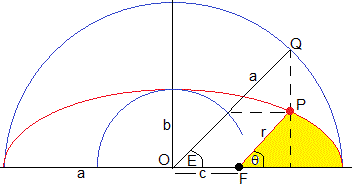
Trazamos la trayectoria elíptica de semieje mayor a y excentricidad ε en color rojo. c=ε·a es la semidistancia focal entre O y el foco F donde se encuentra el Sol.
Trazamos una circunferencia de radio a en color azul y dibujamos una recta perpendicular al eje mayor que corta a la circunferencia en el punto Q. El ángulo de la recta OQ se denomina E, anomalía excéntrica del planeta en el instante t. Obtenemos la siguiente relación geométrica: acosE=c+rcosθ
A partir de la primera relación entre cosE y cosθ obtenemos la ecuación de la trayectoria en función de E
Que es la ecuación de la trayectoria en términos del ángulo E, que ya hemos obtenido
Utilizando la relación trigonométrica de la tangente del ángulo mitad, llegamos a una relación entre los ángulos E y la posición angular θ
Que es la relación entre los ángulos θ y E obteneida anteriormente
Trayectorias parabólicas
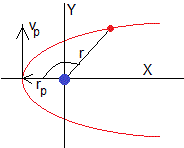
Una trayectoria parabólica se caracteriza por que la energía de la partícula es nula y la excentricidad es ε=1. La ecuación de la trayectoria es
La posición de máximo acercamiento rp al centro de fuerzas se produce para θ=0, por lo que rp=d/2
La posición angular θ en función del tiempo t es
Haciendo estos cambios la integral es inmediata
La ecuación de Kepler para órbitas parabólicas se escribe
Dada la posición θ del cuerpo celeste se calcula el tiempo t. Sin embargo, dado el tiempo t requiere algo más de esfuerzo calcular la posición angular θ como veremos en este ejemplo
Dado el tiempo t determinar la posición angular θ del satélite
Un satélite artificial describe una trayectoria parabólica, su velocidad en el perigeo es de vp=10000 m/s. Determinar la distancia del satélite al centro de la Tierra seis horas más tarde.
Dado vp, aplicamos el principio de conservación de la energía para calcular la distancia más próxima al centro de la Tierra, rp. Para una trayectoria parabólica, la energía total es 0.
El momento angular vale L=m·rp·vp
Dado el instante t, el ángulo θ es la raíz real de la ecuación cúbica
Utilizamos la función raices_3, para obtener las tres raíces de la ecuación cúbica, una real y dos complejas conjugadas. Conocido el ángulo θ, obtenemos la distancia r al centro de la Tierra mediante la ecuación de la trayectoria
Elaboramos un script para realizar los cálculos
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
vp=10000; %velocidad en el perigeo
rp=2*G*M/vp^2; %perigeo
L=rp*vp; %momento angular
t=6*60*60; %instante 6 h
%resolvemos la ecuación cúbica
c=6*G^2*M^2*t/L^3;
x=raices_3([1,0,3,-c]);
th=0;
for i=1:3
if isreal(x(i))
th=2*atan(x(i));
break;
end
end
r=2*rp/(1+cos(th));
disp(r)
La distancia del satálite al centro de la Tierra en el instante t=6 h, en km, es
8.6993e+04
Trayectorias hiperbólicas
La energía total de una partícula que describe una trayectoria hiperbólica es positiva, la excentricidad es ε>1. La posición angular en función del tiempo es
Calculamos la integral, sabiendo que ε>1, para ello seguimos los mismos pasos que para la trayectoria elíptica
con a=(ε-1)/(ε+1)
La primera integral es inmediata
La segunda integral es algo más laboriosa
Haciendo el cambio, u=tanhv, du=dv/cosh2(v),
Deshaciendo los cambios
Se ha utilizado la relación
El resultado de la suma de las dos integrales es
Definimos el ángulo F
La suma de las dos integrales se convierte en
La ecuación de Kepler para trayectorias hipérbólicas es
Donde se ha definido el ángulo F
Para una partícula que viene del infinito con velocidad v0 y parámetro de impacto b, el momento angular L y la energía E valen
La ecuación de Kepler se escribe
Ecuación de la trayectoria en términos del ángulo F
La ecuación de la trayectoria es
la excentricidad ε>1. Conociendo la relación entre los ángulos θ y F
Determinaremos la ecuación de la trayectoria en términos del ángulo E, utilizando las relaciones trigonométricas
El resultado es
Hemos utilizado las relaciones
Finalmente, la ecuación de la trayectoria es
Dada la posición angular θ del satélite determinar el tiempo t

Un satélite artificial tiene un perigeo de 300 km de altura sobre la superficie de la Tierra, llevando una velocidad de 15000 m/s. Calcular la distancia al centro de la Tierra cuando su posición angular es θ=100°.
La ecuación de la hipérbola es
La energía y el momento angular valen
que nos permiten calcular el parámetro d y la excentricidad ε
M=5.98e24; %masa de la Tierra G=6.67e-11; %constante G R=6370000; %radio de la Tierra vp=15000; %velocidad en el perigeo rp=300000+R; %perigeo L=rp*vp; %momento angular E=vp^2/2-G*M/rp; %energía d=L^2/(G*M); e=sqrt(1+2*L^2*E/(G*M)^2);
La excentricidad ε>1, la trayectoria es hiperbólica
>> e e = 2.7625
Calculamos el mayor ángulo θ posible, el ángulo θ∞ de la asíntota
>> acos(-1/e)*180/pi ans = 111.2222
que es un ángulo mayor que θ=100°
Calculamos el ángulo F
La ecuación de Kepler para trayectorias hiperbólicas nos proporciona el instante t en el que el satélite alcanza la posición θ
M=5.98e24; %masa de la Tierra G=6.67e-11; %constante G R=6370000; %radio d ela Tierra vp=15000; %velocidad en el perigeo rp=300000+R; %perigeo L=rp*vp; %momento angular E=vp^2/2-G*M/rp; %energía d=L^2/(G*M); e=sqrt(1+2*L^2*E/(G*M)^2); th=100*pi/180; %posición angular F=2*atanh(sqrt((e-1)/(e+1))*tan(th/2)); t=(e*sinh(F)-F)*L^3/((e^2-1)^(3/2)*(G*M)^2); disp(t/60)
El instante t en minutos es
68.6725
Dada el instante t determinar la posición angular θ del satélite
Completamos este ejemplo, calculando la posición y velocidad del satélite 3 h después de haber pasado por la posición θ=100°, es decir en el instante t=14 920 s
Conocido t, la ecuación de Kepler despejamos F en la ecuación transcendente
Conocido F despejamos la posición angular θ
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
R=6370000; %radio de la Tierra
vp=15000; %velocidad en el perigeo
rp=300000+R; %perigeo
L=rp*vp; %momento angular
E=vp^2/2-G*M/rp; %energía
d=L^2/(G*M);
e=sqrt(1+2*L^2*E/(G*M)^2);
th=100*pi/180; %posición angular
F=2*atanh(sqrt((e-1)/(e+1))*tan(th/2));
t=(e*sinh(F)-F)*L^3/((e^2-1)^(3/2)*(G*M)^2);
t=t+3*3600;
k=(e^2-1)^(3/2)*(G*M)^2*t/L^3;
f=@(x) e*sinh(x)-x-k;
F=fzero(f,[0,5]);
th=2*atan(tanh(F/2)*sqrt((e+1)/(e-1))); %posición angular
r=d/(1+e*cos(th)); %distancia al centro de la Tierra
fprintf('Posición angular %3.1f, distancia al centro %3.1f km\n',
th*180/pi,r/1000)
Posición angular 107.8, distancia al centro 162819.7 km
Para conocer aproximadamente la raíz de la ecuación transcendente, representamos la función f(x)=esinh(x)-x-k
>> fplot(f,[0,5]) >> grid on
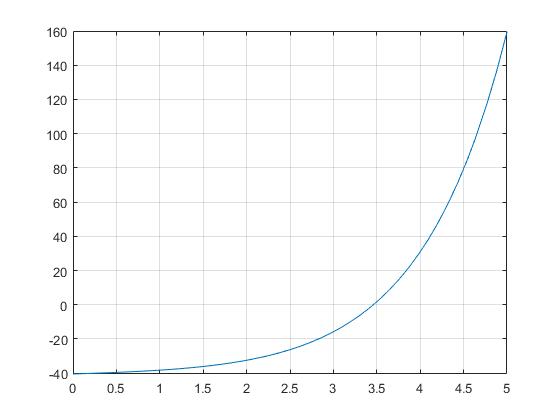
Aproximadamente, F=3.5 rad
Calculamos las componentes de la velocidad a la distancia r=162819.7 km del centro de la Tierra
Cuando la partícula llega al infinito, la energía potencial es nula,
Calculamos las componentes de la velocidad vr y vθ, el módulo de la velocidad v y la comparamos con la velocidad del satélite muy alejado de la Tierra, v∞
>> v_th=L/r v_th = 614.4836 >> v_r=sqrt(2*(E+G*M/r)-v_th^2) v_r = 1.0484e+04 >> sqrt(v_r^2+v_th^2) ans = 1.0502e+04 >> v_inf=sqrt(2*E) v_inf = 1.0266e+04
Completamos el script, trazando la trayectoria hiperbólica y las posiciones del satélite en dos instantes: t1=4 120.3 s y t2=14 920 s
M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
R=6370000; %radio de la Tierra
vp=15000; %velocidad en el perigeo
rp=300000+R; %perigeo
L=rp*vp; %momento angular
E=vp^2/2-G*M/rp; %energía
d=L^2/(G*M);
e=sqrt(1+2*L^2*E/(G*M)^2);
th_1=100*pi/180; %posición angular
F=2*atanh(sqrt((e-1)/(e+1))*tan(th_1/2));
t1=(e*sinh(F)-F)*L^3/((e^2-1)^(3/2)*(G*M)^2);
t2=t1+3*3600;
k=(e^2-1)^(3/2)*(G*M)^2*t2/L^3;
f=@(x) e*sinh(x)-x-k;
F=fzero(f,[0,5]);
th_2=2*atan(tanh(F/2)*sqrt((e+1)/(e-1))); %posición angular
r=d/(1+e*cos(th_2)); %distancia al centro de la Tierra
hold on
f=@(x) d./(1+e*cos(x));
fplot(@(x) f(x).*cos(x), @(x) f(x).*sin(x),[0,acos(-1/e)])
plot(f(th_1)*cos(th_1),f(th_1)*sin(th_1),'bo','markersize',3,'markeredgecolor'
,'b','markerfacecolor','b')
line([0,f(th_1)*cos(th_1)],[0,f(th_1)*sin(th_1)],'lineStyle','--','color','b')
plot(f(th_2)*cos(th_2),f(th_2)*sin(th_2),'ro','markersize',3,'markeredgecolor'
,'r','markerfacecolor','r')
line([0,f(th_2)*cos(th_2)],[0,f(th_2)*sin(th_2)],'lineStyle','--','color','r')
grid on
xlabel('x')
ylabel('y')
title('Trayectoria hiperbólica')
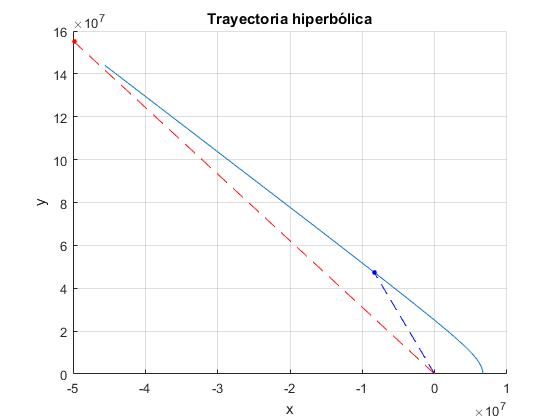
Dada la posición radial r del satélite determinar el tiempo t
Expresamos la energía del cuerpo celeste de masa m en términos de la distancia radial r al centro de fuerzas
Para un cuerpo celeste que describe una trayectoria hiperbólica, E>0, es la energía cinética en el infinito (la potencial es nula)
Establecemos el tiempo t=0, cuando el cuerpo celeste pasa por la posición más cercana al centro de fuerzas, a una distancia rp. La componente radial de la velocidad en esta posición es nula, dr/dt=0
En la expresión de la energía despejamos dt e integramos
Resolvemos la integral
Descomponemos la integral en suma de dos
La primera es inmediata y en la segunda, completamos cuadrados
Ahora resolvemos la integral definida entre rp posición más cercana y r
El resultado final es
M=5.98e24; %masa de la Tierra G=6.67e-11; %constante G R=6370000; %radio de la Tierra vp=15000; %velocidad en el perigeo rp=300000+R; %perigeo L=rp*vp; %momento angular E=vp^2/2-G*M/rp; %energía d=L^2/(G*M); e=sqrt(1+2*L^2*E/(G*M)^2); th=100*pi/180; %posición angular r=d/(1+e*cos(th)); %distancia al centro de la Tierra F=2*atanh(sqrt((e-1)/(e+1))*tan(th/2)); t1=(e*sinh(F)-F)*L^3/((e^2-1)^(3/2)*(G*M)^2); vi=sqrt(2*E); %velocidad en el infinito t2=(G*M/vi^3)*(sqrt((1+r*vi^2/(G*M))^2-(1+rp*vi^2/(G*M))^2)- acosh((1+r*vi^2/(G*M))/(1+rp*vi^2/(G*M)))); disp([t1,t2])
Los tiempos calculados para la posición angular θ=100°, o para la distancia radial r=4.8235e·107 m son los mismos 4 120.3 s
1.0e+03 * 4.1203 4.1203
Referencias
Howard D. Curtis. Orbital Mechanics for Engineering Students. Elsevier, capítulo 3

