Dinamika

Marruskadura-indarra

Irristatzearen
marruskadura

Koefiziente zinetikoa
neurtzen (I)

Koefiziente zinetikoa
neurtzen (II)

Koefiziente zinetikoa
neurtzen (III)

Marruskadura-indarra
plano inklinatuan

Bloke bat arrastatzeko
angelu egokiena

Koefiziente estatikoa
neurtzen

 Habe bat, euskarri
mugikor bitan etzanda

Xafla bat, gurpil
birakor bitan etzanda.

Bloke bi
elkarren gainean

Adibidea

Saiakuntza

Erreferentzia

Orri honetan aztertuko den adibidean, habe bat euskarri bitan etzanda dago eta euskarriok elkarrenganantz mugitzen dira abiadura konstanteaz.

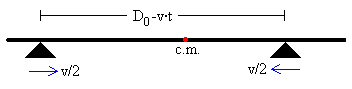
Euskarriak mugitzean habearen pisua banatu egiten da eta lehenik batek irristatzen du eta gero besteak baina ez biak batera. Esaterako, ezkerreko euskarriak irristatzen badu (1-ek) orduan eskumakoa (2-a) geldi egongo da, eta alderantziz. Marruskadura-indarrak berezkoa du portaera berezi hori.

• Marruskadura-indarra, kontaktu-gainazalean bertan gauzatzen da.

• Marruskadura indarra gorputzaren oreka-baldintzen arabera aldatzen da.

• Gorputz bat irristatzera doan unean marruskadura indarraren balioa maximoa da: f_r=μ_s·N

• Gorputza irristatzen ari denean marruskadura indarraren balioa hau da:  f_r=μ_k·N, eta hemen N  indar normala da, edo kontaktuan dauden gainazal bien arteko indar zapaltzailea.

• Koefiziente estatiko eta zinetikoa, μ_s eta μ_k, enpirikoak dira eta gainazal bietako molekulen arteko interakzio konplexuen araberakoak dira.

Deskribapena

Demagun hasieran euskarri bien artean D₀ distantzia dagoela, baina euskarri biak v/2 abiadura konstanteaz hurbiltzen badira, t denbora iragan ondoren, hona euren arteko distantzia: D=D₀ -v·t.

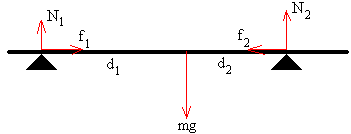
Demagun bitarteko egoera bat: ezkerreko euskarriaren posizioa habearen masa-zentroarekiko d₁, eta eskumako euskarriaren posizioa  d₂=D-d₁. Irudika dezagun habeak jasaten dituen indarrak eta aplika ditzagun oreka-baldintzak.

1. Indar guztien erresultantea nulua izan behar da.

N₁+N₂=mg

Hemen N₁ ezkerreko euskarriak egiten dio habeari eta N₂ eskumakoak.

2. Indarren momentu totala nulua izan behar da, edozein punturekiko. Aukera dezagun eskumako euskarria erreferentzia gisa:

-N₁·(d₁+d₂)+mg·d₂=0

Ekuazio bi eta ezezagun bi ditugu, N₁ eta N₂ , beraz kalkulua burutuz:

• Ezkerreko euskarria eskumarantz mugitzean marruskadura-indarra sortuko du: f₁, habea eskumarantz bultzatzen.

• Eta eskumako euskarria ezkerrerantz mugitzean f₂ marruskadura-indarra sortuko du, habea ezkerrerantz bultzatzen.

Marruskadura-indar horiek berdinak izan behar dira: f₁=f₂

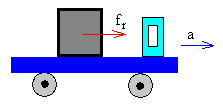Indar bi horien noranzkoa hobeto ulertzeko, azter dezagun kamioi batek bere plataforman kutxa bat garraiatzen duela. Kamioia pausagunetik abiatzen denean, kutxak jasaten duen marruskadura-indarra fr=ma izan behar da (a kamioiaren azelerazioa eta m kutxaren masa), eta indar horrek eramaten du kutxa kamioiarekin batera eta plataformaren gainean irristatu gabe (irristatzen ez badu fr< μs·N  izan behar da). Kamioiaren a azelerazioak balio jakin bat gainditzen badu, kutxa plataformarekiko irristatzen hasiko da. Orduan, marruskadura-indarra honakoa izango da: fr= μk·N.

Habearen analisira itzuliz, azter ditzagun habearen higidura posibleak bi euskarrien jokabidearen arabera:

1. Demagun ezkerreko euskarriak irristatzen duela eta eskumakoa ordea, habearekiko geldi mantentzen dela.

Habearen eta euskarri bien arteko marruskadura-indarrak hauek dira:

f₁=μ_k·N₁
f₁=f₂< μ_s·N₂

Lehen kasu honetan, d₁ distantzia gutxitzen ari da eta d₂ distantzia ordea, konstante mantentzen da. Beraz, N₁ handitzen joango da eta N₂ gutxitzen, eta halako batean, marruskadura-indarraren balio maximoa atzemango da: f₂=μ_s·N₂. Une horretan eskumako euskarria irristatzen hasiko da, eta ezkerrekoa gelditu.

Kalkula dezagun euskarri bien arteko distantzia (D₁=d₁+d₂) baldintza hori betetzen denean:

μ_k·N₁= μ_s·N₂, edo
μ_k·d₂= μ_s·d₁

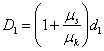
2. Demagun eskumako euskarriak irristatzen duela eta ezkerrekoa ordea, habearekiko geldi mantentzen dela.

f₂=μ_k·N₂
f₂=f₁< μ_s·N₁

Oraingoan eskumako euskarriaren d₂ distantzia gutxitzen ari da eta d₁ distantzia ordea, konstante mantentzen da. Beraz, N₂ handitzen joango da eta N₁ gutxitzen, eta halako batean, marruskadura-indarraren balio maximoa atzemango da: f₁=μ_s·N₁. Une horretan ezkerreko euskarria irristatzen hasiko da, eta eskumakoa gelditu.

Kalkula dezagun euskarri bien arteko distantzia (D₁=d₁+d₂) baldintza hori betetzen denean:

μ_s·N₁= μ_k·N₂, edo,
μ_s·d₂= μ_k·d₁.

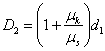
1 eta 2 kasuetako distantziak (D₁ eta D₂) ez dira berdinak eta bien arteko erlazioa hau da:

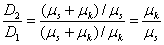
Prozesua behin eta berriz errepikatzen da eta distantzia kontsekutibo biren arteko erlazioa (D_n+1 eta D_n) hori bera da:

Adibidea

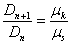
• Ezkerreko euskarriaren posizioa masa-zentroarekiko, d₁=50 cm

• Eskumako euskarriaren posizioa masa-zentroarekiko, d₂=45 cm

• Marruskadura koefiziente estatikoa, μ_s=1.0

• Marruskadura koefiziente zinetikoa, μ_k=0.8

• Habearen masa, mg=1.0 N

• Euskarrien abiadura erlatiboa hurbiltzean, v=1.0 cm/s

1. Ezkerreko euskarriak irristatzen du eta eskumakoak ez:

d₁ distantzia gutxitzen doa, d₁=50-1·t  (cm).

d₂ distantzia konstante mantentzen da:  d₂=45 cm

Marruskadura-indarra: f₂=f₁=μ_k·N₁

d₁ gutxitzen ari denez, N₁ handitzen doa. Noiz arte? Ba f₂-ren balioa maximora iristen den arte: f₂=μ_s·N₂,  une horretan eskumako euskarria irristatzen hasten da, eta ezkerrekoa gelditu.

μ_k·N₁=μ_s·N₂. edo  μ_k·d₂=μ_s·d₁

0.8·45=1.0·d₁,   d₁=36 cm

Euskarri bien arteko distantzia hau da: D₁=d₁+d₂=45+36=81 cm

Posizio horretara iristeko denbora:  36=50-t,   t=14 s

2. Eskumako euskarriak irristatzen du eta ezkerrekoak ez:

d₂ distantzia gutxitzen doa, d₂=45-1·(t-14)  (cm).

d₁ distantzia konstante mantentzen da:  d₁=36 cm

Marruskadura-indarra:  f₁=f₂=μ_k·N₂

d₂ gutxitzen ari denez, N₂ handitzen doa. Noiz arte? Ba  f₁-en balioa maximora iristen den arte: f₁=μ_s·N₁, une horretan ezkerreko euskarria irristatzen hasten da eta eskumakoa gelditu.

μ_s·N₁=μ_k·N₂. edo,  μ_s·d₂=μ_k·d₁

1.0·d₂=0.8·36,     d₂=28.8 cm

Euskarri bien arteko distantzia hau da: D₂=d₁+d₂=36+28.8=64.8 cm

Posizio horretara iristeko denbora:  28.8=45-(t-14), t=30.2 s

Distantzia bien arteko erlazioa D₂/D₁=64.8/81, hain zuzen, marruskadura-koefizienteen erlazioaren berdina da: zinetikoa μ_k=0.8 eta estatikoa μ_s=1.0.

3. Ezkerreko euskarriak irristatzen du eta eskumakoak ordea, ez.

Deskribapen osoa lehen atalaren berdina da.

4. Eskumako euskarriak irristatzen du eta ezkerrekoak ordea, ez.

Deskribapen osoa lehen atalaren berdina da. Eta behin eta berriz aldatzen segituko du.

Saiakuntza

Berria botoia sakatu.

• Euskarri bien arteko distantzia hasieran finkatu; ezkerrekoa finkoa da, baina eskumakoa (gorria) saguarekin desplazatzen da.

Idatzi

• Habearen eta euskarrien arteko μ_k  marruskadura-koefiziente zinetikoa dagokion desplazamendu-barrari saguaz eragiten.

Hasi botoia sakatu.

Programa interaktiboak finkotzat hartu ditu ondoko balio guztiak:

• Marruskadura-koefiziente estatikoa: μ_s=1.0

• Habearen luzera:  100 cm

• Euskarrien abiadura erlatiboa hurbiltzen ari direnean v=1 cm/s. Alegia, ezkerreko euskarria eskumarantz desplazatzen da 0.5 cm/s-ko abiaduraz, eta eskumakoa ere abiadura beraz baina ezkerrerantz.

• Habearen masa, mg, unitatea hartu da.

Euskarri biak hurbiltzen direla behatzen da, eta habea bietariko batekin desplazatzen dela. Noizean behin euskarri batetik bestera aldatzen da. Applet-aren eskumako aldean, ardatz bertikal batean, euskarrien arteko D distantzia adierazten da justu euskarri-aldaketa gertatzen denean: D₁, D₂, … D_n alegia, irristatzea euskarri batetik bestera pasatzen denean. Simulazioan, euskarrien arteko distantzia D=10 cm. denean gelditu egiten da.

Euskarri bakoitzaren azpian indar normala adierazten da, N₁ eta N₂ .

Applet-aren goiko eta ezkerreko aldean denbora eta euskarri bien posizioak adierazten dira masa-zentroarekiko: d₁ eta d₂ .

Azkenik, goiko eta eskumako aldean, habearen eta euskarri bakoitzaren arteko marruskadura-indarra: f₁=f₂= μ_k·N₁,₂.  Nola oszilatzen duen ikusten da.