Dinamika

Marruskadura-indarra

Irristatzearen
marruskadura

Koefiziente zinetikoa
neurtzen (I)

Koefiziente zinetikoa
neurtzen (II)

Koefiziente zinetikoa
neurtzen (III)

Marruskadura-indarra
plano inklinatuan

Bloke bat arrastatzeko
angelu egokiena

Koefiziente estatikoa
neurtzen

Habe bat, euskarri
mugikor bitan etzanda

 Xafla bat, gurpil
birakor bitan etzanda

Bloke bi
elkarren gainean

Adibideak

Saiakuntza

Erreferentzia

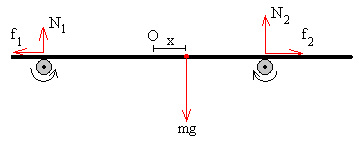
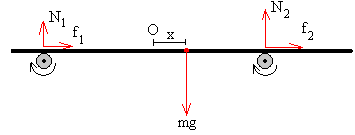
Xafla horizontal bat gurpil biren gainean etzanda dago eta gurpilek biratu egiten dute. Xaflaren m masa ezaguna da, gurpilen arteko distantzia 2a eta xaflaren masa-zentroa hasieran justu gurpilen erdian dago. Xaflaren eta gurpilen arteko marruskadura koefizientea μ da.

Deskribapena

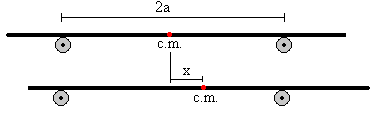
Demagun xaflaren masa-zentroa bere oreka posiziotik desplazatu egiten dela x distantzia eskumarantz. Irudika ditzagun xaflak jasaten dituen indar guztiak eta aplika ditzagun oreka-baldintzak:

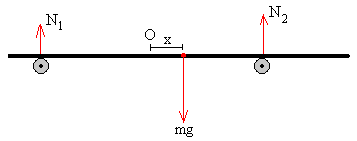
1. Norabide bertikalean:

N₁+N₂=mg

Ezkerreko gurpilak xaflari egiten dion indar normala N₁ eta eskumakoa N₂.

2. Indarren momentu totala nulua izan behar da, edozein punturekiko. Har dezagun erreferentziatzat eskumako gurpila bera.

-N₁·2a+mg·(a-x)=0

Ezezagun bi ditugu, N₁ eta N₂, eta ekuazio bi, beraz kalkula daitezke:

Marruskadura indarrak

Gurpilek biratzean xaflarekin dituzten kontaktuek irristatu egingo dute.

Kontaktuetako marruskadura indarrak honakoak dira:  f₁=μ·N₁ eta  f₂=μ·N₂ eta noranzkoak gurpilen biraketaren aldekoak:

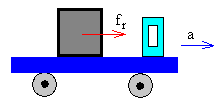Indar bi horien noranzkoa hobeto ulertzeko, azter dezagun kamioi bat bere plataforman kutxa bat garraiatzen. Kamioia pausagunetik abiatzen denean, kutxak jasaten duen marruskadura-indarra fr=ma izan behar da (a kamioiaren azelerazioa eta m kutxaren masa), eta indar horrek eramaten du kutxa kamioiarekin batera eta plataformaren gainean irristatu gabe (irristatzen ez badu fr< μs·N  izan behar da).

Kamioiaren a azelerazioak balio jakin bat gainditzen badu (marruskadura indarrari  μ_s·N, balioa gainditzea eskatzen diona) kutxa plataformarekiko irristatzen hasiko da. Orduan marruskadura-indarra honakoa izango da: f_r= μ_k·N. Kamioiaren azelerazioa a da baina kutxarena a_c=f_r/m= μ_k·g.  Hortaz, kutxaren azelerazio erlatiboa kamioiarekiko kenketa da: a_c- a.

Xaflaren higiduraren ekuazioak

Azter ditzagun gerta daitezkeen zenbait kasu ezberdin:

1. Gurpil biek barrurantz biratzen dute:

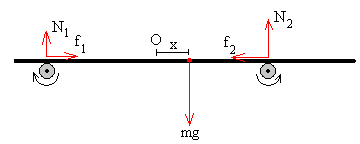
Barrurantz biratzea da, ezkerreko gurpila erlojuaren orratzen alde eta eskumakoa erlojuaren orratzen aurka. Marruskadura-indarrek,  f₁ eta f₂ , irudiak adierazten duen noranzkoak dituzte, barrurantz alegia. Beraz xaflak jasaten duen indar horizontal totala hau da:

f=f₁-f₂= μ·N₁ - μ·N₂= -(μmg/a)·x

Xaflak jasaten duen f  indar horizontala, bere x desplazamenduaren proportzionala da eta desplazamenduaren aurkakoa. Honelako indar baten eraginpean, higidura harmoniko sinpleaz mugituko da. Hona dagokion ekuazio diferentziala:

 

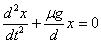
Ekuazio horren koefizienteak Higidura Harmoniko Sinplearen maiztasun angeluarra ematen du: ω²=μg/a, eta periodoa:

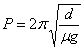
Ekuazio diferentzialaren soluzioa:

x=A·sin(ωt+φ)

A anplitudea eta φ hasierako fasea, hasierako baldintzetatik definitzen dira.

2. Gurpil biek kanporantz biratzen dute

Kanporantz biratzea da, ezkerreko gurpila erlojuaren orratzen aurka eta eskumakoa erlojuaren orratzen alde. Marruskadura-indarrek,  f₁ eta f₂ , irudiak adierazten duen noranzkoak dituzte, kanporantz alegia. Beraz xaflak jasaten duen indar horizontal totala hau da:

f=f₂ -f₁= μ·N₂ - μ·N₁=(μmg/a)·x

Xaflak jasaten duen f  indar horizontala, bere x desplazamenduaren proportzionala da baina desplazamenduaren aldekoa.  Hona dagokion ekuazio diferentziala:

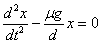
Hori ez da HHS baten ekuazio diferentziala. Ekuazio horren soluzioa honelakoa da:

x=A·exp(ωt)+B·exp(-ωt)

esponentzial gorakor bat eta beherakor bat, eta hemen A eta B, hasierako baldintzetatik definitzen dira.

 

3. Gurpil biek noranzko berean biratzen dute

Bi gurpilek noranzko berean biratzen badute, marruskadura-indarrek,  f₁ eta f₂ , irudiak adierazten duen noranzkoak dituzte, biak eskumarantz. Beraz xaflak jasaten duen indar horizontal totala hau da:

f=f₂+f₁= μ·N₂+ μ·N₁= μmg

Xaflak jasaten duen f  indar horizontala konstantea da. Beraz xaflaren azelerazioa konstantea izango da: higidura uniformeki azeleratua

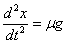
Eta bere soluzioa:

x=x₀+v₀·t+μgt²/2

Hemen x₀ eta v₀ hasierako posizioa eta abiadura dira: t=0 aldiunean.

Adibideak

Har ditzagun finkotzat:

a=40 cm
μ=0.8

1. Gurpilek barrurantz biratzen dute:

Lehenago burututako kalkuluek erakusten dute oszilazioen periodoa hau dela:

Har ditzagun anplitudea eta hasierako fasea honakoak: A=10 cm, φ=0. Beraz xaflaren masa-zentroaren posizioa:

x=10·sin(4.43·t) cm

Hona abiadura:

v=dx/dt=A·ω·cos(ωt+φ)

Hasierako aldiunean, t=0, xaflaren posizioa x₀=0 da eta abiadura v₀=10·4.43=44.3 cm/s.

2. Gurpilek kanporantz biratzen dute:

x=A·exp(ωt)+B·exp(-ωt)

v=dx/dt= A·ω·exp(ωt) -B·ω·exp(-ωt)

Xaflak zein higidura-mota izango duen, hasierako baldintzen araberakoa da. Baldin A=0, xaflak oreka posiziorantz jotzen du, x=0-rantz, denbora iragaten den heinean. Baina A ez bada nulua, x posizioa denborarekiko etengabe handitzen da, edo hobeto esanda, xaflaren ertza gurpil baten gainetik erortzen den arte, edo masa zentroa gurpil bien artetik irteten den arte. Azken egoera ezegonkorra da eta xafla irauli egingo da.

Simulazioan aukeratu diren hasierako baldintzek, A=0 bermatzen dute.

Beraz: t=0, x₀=B, v₀= -B·ω

3. Gurpilek noranzko berean biratzen dute

Xaflaren masa-zentroaren posizioa denboraren menpe,

x=x₀+v₀·t+μgt²/2

Simulazioan aukeratu diren hasierako baldintzak honakoak dira: t=0, x₀=0, v₀=0, hortaz:

x= μgt² /2

Kasu honetan, xaflaren ertza gurpil baten gainetik eroriko den unean edota masa-zentroa gurpil bien artetik irteten denean simulazioa gelditu egiten da.

Saiakuntza

Berria botoia sakatu.

• Eskumako gurpila (gorria) saguaz desplazatu daiteke, eta ezkerrekoa berarekiko simetrikoki mugitzen da. Azkenean bi gurpilen arteko distantzia 2a da.

• Marruskadura-koefizientea aukeratu behar da, μ, desplazamendu barrari saguaz eragiten.

Gurpil bien noranzkoa aukera daiteke honako aukera hauetatik:

1. Gurpil biak elkarren kontra biratuz, Barrurantz.

2. Gurpil biak elkarren kontra biratuz, Kanporantz.

3. Gurpil biak elkarren alde biratuz, Noranzko bera.

Hasi botoia sakatu eta xafla nola mugitzen den behatu.

Gelditu/Jarraitu/Pausoka botoiak erabilita mugimendua zehazkiago beha daiteke, esaterako, lehen kasuan, oszilazioen periodoa neurtzeko.