Declaración de variables simbólicas

La herramienta Symbolic Math Toolbox define un nuevo tipo de dato denominado objeto simbólico, que representan a variables, expresiones y matrices.

El comando sym se usa para crear objetos simbólicos en MATLAB. El argumento de sym es una cadena de caracteres (string) entre comillas simples. Por ejemplo,

>> sym('x')
>> sym('2')
>> sym('1/3')

Hemos creado tres objetos simbólicos, x es una variable, 2 es un número y 1/3 es una fracción. Vamos a apreciar la diferencia entre operar con números a operar con objetos simbólicos.

>> sqrt(2)
ans =    1.4142
>> sqrt(sym('2'))
ans =2^(1/2)
>> 2/3+1/2
ans =    1.1667
>> sym('2/3')+sym('1/2')
ans =7/6
>> sin(pi)
ans =  1.2246e-016
>> sin(sym('pi'))
ans =0

En la última línea, vemos claramente la diferencia entre los valores que devuelve el seno de π.

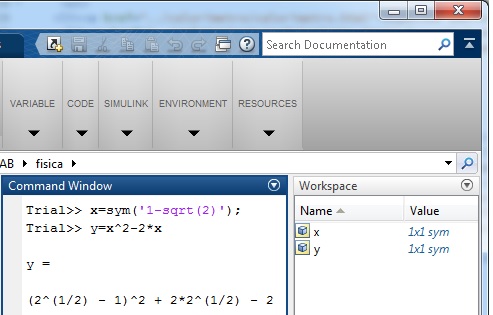
Supongamos que queremos evaluar una función f(x) para un determinado valor de x

${\displaystyle \begin{array}{l}y=x^2-2x\\ x=1-\sqrt{2}\\ y={\left(1-\sqrt{2}\right)}^2-2\left(1-\sqrt{2}\right)\end{array}}$

>> x=sym('1-sqrt(2)');
>> y=x^2-2*x
y =(2^(1/2) - 1)^2 + 2*2^(1/2) - 2
>> simplify(y)
ans =1

sym nos permite crear y dar un valor inicial a una variable simbólica x.

Se ha creado una variable simbólica x y otra variable simbólica y, tal como puede verse en la ventana Workspace. El comando simplify que estudiaremos más adelante simplifica la expresión resultante.

El comando syms permite declarar más de una variable simbólica y no precisa de comillas simples, por lo que se utilizará con mayor frecuencia.

>> syms x y;
>> s=x+2*y-x
s =2*x
>> r=sqrt(x^2+y^2);

Se han creado dos variables simbólicas nuevas s y r tal como podemos apreciar en la ventana Workspace. s=x+2*y+x, r=sqrt(x^2+y^2), son ejemplos de expresiones simbólicas.

Funciones que trabajan con expresiones simbólicas.

Vamos ahora a estudiar las funciones que trabajan con expresiones simbólicas

expand

Realiza operaciones con expresiones simbólicas tal como vemos en el siguiente ejemplo

${\displaystyle y={(x-1)}^3+3x^2+1}$

>> syms x;
>> y=(x-1)^3+3*x^2+1;
>> expand(y)
ans =x^3 + 3*x
>> y=exp(x+x^2);
>> expand(y)
ans =exp(x^2)*exp(x)

Se ha declarado una variable simbólica x con syms y se crea una variable simbólica y y otra variable simbólica, por defecto, ans donde se guarda el resultado de expand.

collect

Ordena los términos en potencias de x

>> syms x;
>> y=x*(cos(x)+x)*(exp(x)+x^2);
>> collect(y)
ans =x^4 + cos(x)*x^3 + exp(x)*x^2 + (exp(x)*cos(x))*x

simplify

La función simplify se utiliza con frecuencia en los cálculos con expresiones algebraicas.

${\displaystyle \left(x^2-x+\frac{1}{x}-\frac{1}{x^2}\right):\left(x-1+\frac{1}{x}\right)}$

>> syms x;
>> y=(x^2-x+1/x-1/x^2)/(x-1+1/x);
>> simplify(y)
ans =x - 1/x 

En la página, Sistema de ecuaciones diferenciales lineales, realizaremos largas operaciones con expresiones algebraicas, por ejemplo

${\displaystyle \begin{array}{l}x=\frac{-80+25i}{16}·\frac{1-8i}{5}{e}^{(2-8i)t}-\frac{80+25i}{16}·\frac{1+8i}{5}{e}^{(2+8i)t}=\\ x=\frac{1}{8}{e}^{2t}\left(24\cos (8t)+\frac{133}{8}\sin (8t)\right)\end{array}}$

>> syms t;
>> x=(-80+25*i)*(1-8*i)*exp((2-8*i)*t)/80-(80+25*i)*(1+8*i)*exp((2+8*i)*t)/80;
>> simplify(x) 
ans =(exp(2*t)*(24*cos(8*t) + 133*sin(8*t)))/8

Como ejercicio se sugiere, simplificar las siguientes expresiones

${\displaystyle \begin{array}{l}\left(\frac{x}{y^3}-\frac{1}{y^2}\right)\left(\frac{x-y}{y}+\frac{2x}{x-y}-\frac{x^2}{xy-y^2}\right)\\ \left(\frac{3}{x+y}\right)\left(\frac{x^2}{y^2}-1\right)\left(\frac{x+y}{x-y}-\frac{x-y}{x+y}\right)\end{array}}$

factor

Como su nombre indica, factoriza una expresión

Primero vamos a probar con números y a continuación, con expresiones simbólicas

${\displaystyle 360=2^5·3^2·5}$

>> factor(360)
ans =
     2     2     2     3     3     5
>> factor(sym('360'))
ans =2^3*3^2*5 

${\displaystyle y=x^8-2x^6-9x^4+2x^2+8}$

>> syms x;
>> factor(x^8-2*x^6-9*x^4+2*x^2+8)
ans =(x - 1)*(x - 2)*(x + 2)*(x + 1)*(x^2 + 2)*(x^2 + 1)

subs

Evalúa numéricamente una expresión simbólica, para un determinado valor de la variable simbólica x.

>> syms x;
>> y=x^8-2*x^6-9*x^4+2*x^2+8;
>> subs(y,x,2)
ans =     0
>> subs(y,x,-0.5)
ans =    7.9102

Valores que se asignan a los parámetros a, b y c para resolver una determinada ecuación de segundo grado. Una tabla de valores de la función y=x²-x-6.

>> syms a b c x;
>> y=a*x^2+b*x+c;
>> yy=subs(y,{a,b,c},{1 -1 -6})
yy =x^2 - x - 6
>> subs(yy,[-2:0.5:2])
ans =
         0   -2.2500   -4.0000   -5.2500   -6.0000   -6.2500   -6.0000
   -5.2500   -4.0000

Una variable simbólica puede ser sustituida por otra variable simbólica. Por ejemplo, la variable x se sustituye por u+v y la variable y se sustituye por u-v.

>> syms x y;
>> z=x^2-y^2;
>> syms u v;
>> z=subs(z,{x,y},{u+v,u-v})
z =(u + v)^2 - (u - v)^2
>> simplify(z)
ans =4*u*v

Presentación de resultados

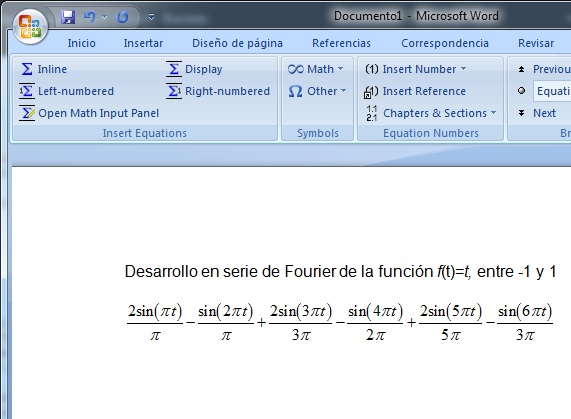
En el capítulo Series de Fourier vamos a obtener el desarrollo en serie de Fourier de funciones periódicas. El resultado del cálculo no es fácilmente legible

syms t k P n;
assume(k,'Integer');
a = @(f,t,k,P) int(f*cos(k*pi*t/P),t,-P,P)/P;
b = @(f,t,k,P) int(f*sin(k*pi*t/P),t,-P,P)/P;
fs=@(f,t,n,P) a(f,t,0,P)/2+symsum(a(f,t,k,P)*cos(k*pi*t/P)
+b(f,t,k,P)*sin(k*pi*t/P),k,1,n);
f=t;
P=1;
N=6; %términos del desarrollo en serie
z=fs(f,t,N,P)

z =(2*sin(pi*t))/pi - sin(2*pi*t)/pi + (2*sin(3*pi*t))/(3*pi)
 - sin(4*pi*t)/(2*pi) + (2*sin(5*pi*t))/(5*pi) - sin(6*pi*t)/(3*pi)

Se mejora la lectura utilizando la función pretty

>> pretty(z)
2 sin(pi t)  sin(2 pi t)  sin(3 pi t) 2  sin(4 pi t)  sin(5 pi t)   2 sin(6 pi t)
---------- - ---------- + ------------ - ----------- + ---------- - ------------
     pi           pi          3 pi         2 pi         5 pi          3 pi

Se mejora aún más, si utilizamos la función latex en combinación con el programa MathType.

>> latex(z)
ans =
\frac{2\, \sin\!\left(\pi\, t\right)}{\pi} - \frac{\sin\!\left(2\, \pi\, t\right)}
{\pi} + \frac{2\, \sin\!\left(3\, \pi\, t\right)}{3\, \pi} - 
\frac{\sin\!\left(4\, \pi\, t\right)}{2\, \pi} + \frac{2\, \sin\!\
left(5\, \pi\, t\right)}{5\, \pi} - \frac{\sin\!\left(6\, \pi\, t\right)}{3\, \pi}

Copiamos el código (cuatro últimas líneas), lo pegamos en MathType que lo convierte en una expresión algebraica completamente legible, la insertamos en el documento Word, seleccionado en el menú File/Update Documento1. El resultado es el que aparece en la figura