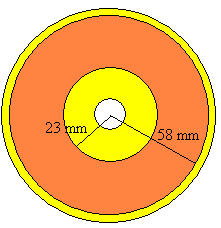
Un disco compacto CD tiene 6 cm de radio, 1.2 mm de espesor con un agujero central de 7.5 mm de radio. La información digital se graba en una espiral de Arquímedes de paso h constante

${\displaystyle r=r_0+\frac{h}{2\pi }\theta }$

La pista más cercana al eje tiene un radio R₀=23 mm y la más alejada R_f=58 mm, h=1.6μm es la separación entre pistas. El número de pistas (vueltas) es, por tanto.

${\displaystyle N=\frac{r_f-r_0}{h}=\frac{58-23}{0.0016}=21875}$

El tiempo total que se emplea en leer a velocidad (lineal) constante la totalidad de las pistas del disco es T=72 min.

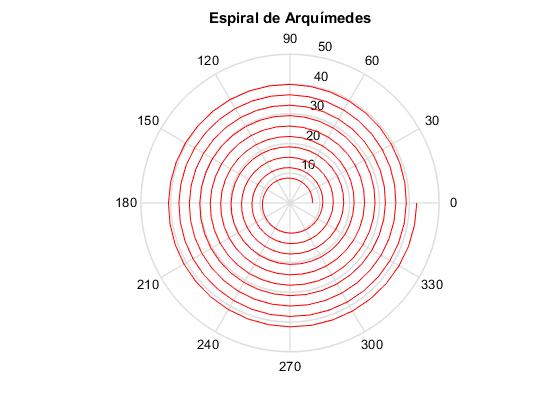
En la figura, por razón de claridad se representa un CD de N=10 pistas, separadas h=3.5 mm.

r0=7.5; 
h=3.5; 
ang=0:pi/18:10*2*pi;
r=r0+h*ang/(2*pi);
polar(ang,r,'r')
title('Espiral de Arquímedes')

Otra forma alternativa de trazar la esperal de Arquímedes

r0=7.5; 
h=3.5; 
r=@(x) r0+h*x/(2*pi);
fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0,10*pi])
axis off
axis equal
title('Espiral de Arquímedes')

Longitud de una espiral de Arquímedes

Vamos a obtener la longitud s de una espiral de Arquímedes por tres métodos distintos, uno exacto y dos aproximados. El primer método nos permite practicar el cálculo integral en particular, las funciones sinh, seno hiperbólico y cosh, coseno hiperbólico.

${\displaystyle s={\displaystyle \underset{A}{\overset{B}{\int }}\sqrt{d{x}^2+d{y}^2}}}$

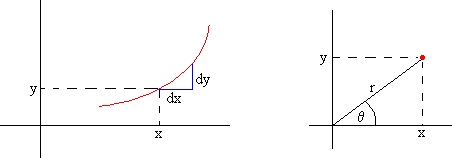
• Cálculo exacto

En coordenadas polares

x=r·cosθ
y=r·sinθ

dx=cosθ·dr-rsinθ·dθ
dy=sinθ·dr-rcosθ·dθ

${\displaystyle s={\displaystyle \underset{A}{\overset{B}{\int }}\sqrt{d{r}^2+r^{2}d{\theta }^2}}}$

En el caso de la espiral de Arquímedes

${\displaystyle r=R_0+\frac{h}{2\pi }\theta dr=\frac{h}{2\pi }d\theta }$

Para calcular la longitud de la espiral se integra entre θ=0, y θ=2πN, donde N es el número de pistas.

${\displaystyle s={\displaystyle \underset{0}{\overset{2\pi N}{\int }}\sqrt{\frac{h^2}{4{\pi }^2}+{\left(R_0+\frac{h}{2\pi }\theta \right)}^2}}d\theta =\frac{2\pi }{h}{\displaystyle \underset{0}{\overset{2\pi N}{\int }}\sqrt{\frac{h^2}{4{\pi }^2}+{\left(R_0+\frac{h}{2\pi }\theta \right)}^2}}\left(\frac{h}{2\pi }d\theta \right)}$

Para resolver la integral del tipo

${\displaystyle {\displaystyle \int \sqrt{a^2+u^2}du}u=R_0+\frac{h}{2\pi }\theta a=\frac{h}{2\pi }}$

se hace el cambio de variable

u=a·sinht, du=acosht

${\displaystyle \begin{array}{l}{\displaystyle \int \sqrt{a^2+u^2}du}={\displaystyle \int a·\cosh t·a·\cosh t·dt=a^2{\displaystyle \int {\cosh }^2}}t·dt=\\ a^2{\displaystyle \int \frac{\cosh (2t)+1}{2}}dt=\frac{a^2}{2}\left(\frac{1}{2}\text{sinh(2}t)+t\right)=\frac{a^2}{2}\left(\text{sinh}t·\cosh t+t\right)\end{array}}$

Deshaciendo el cambio de variable

${\displaystyle \sinh t=\frac{u}{a}\cosh t=\frac{\sqrt{a^2+u^2}}{a}{e}^t=\cosh t+\sinh t=\frac{u+\sqrt{a^2+u^2}}{a}}$

La función integrando es

${\displaystyle {\displaystyle \int \sqrt{a^2+u^2}du}=\frac{u}{2}\sqrt{a^2+u^2}+\frac{a^2}{2}\ln \left(u+\sqrt{a^2+u^2}\right)-\frac{a^2}{2}\ln a}$

El resultado final de la longitud de la espiral de Arquímedes es

${\displaystyle \begin{array}{l}s={\displaystyle \underset{0}{\overset{2\pi N}{\int }}\sqrt{\frac{h^2}{4{\pi }^2}+{\left(R_0+\frac{h}{2\pi }\theta \right)}^2}}d\theta =\\ \frac{2\pi }{h}\left({\begin{array}{l}\frac{1}{2}\left(R_0+\frac{h}{2\pi }\theta \right)\sqrt{\frac{h^2}{4{\pi }^2}+{\left(R_0+\frac{h}{2\pi }\theta \right)}^2}+\\ \frac{h^2}{8{\pi }^2}\ln \left(\left(R_0+\frac{h}{2\pi }\theta \right)+\sqrt{\frac{h^2}{4{\pi }^2}+{\left(R_0+\frac{h}{2\pi }\theta \right)}^2}\right)-\frac{h^2}{8{\pi }^2}\ln \left(\frac{h}{2\pi }\right)\end{array}|}_0^{2\pi N}\right)|\\ =\frac{2\pi }{h}\{\begin{array}{l}\frac{1}{2}{R}_f\sqrt{\frac{h^2}{4{\pi }^2}+R_f^2}+\frac{h^2}{8{\pi }^2}\ln \left(R_f+\sqrt{\frac{h^2}{4{\pi }^2}+R_f^2}\right)\\ -\frac{1}{2}{R}_0\sqrt{\frac{h^2}{4{\pi }^2}+R_0^2}-\frac{h^2}{8{\pi }^2}\ln \left(R_0+\sqrt{\frac{h^2}{4{\pi }^2}+R_0^2}\right)\end{array}\end{array}}$

Introduciendo los datos en el resultado final

${\displaystyle \begin{array}{l}s=\frac{2\pi }{0.0016}\{\begin{array}{l}\frac{1}{2}58\sqrt{\frac{{0.0016}^2}{4{\pi }^2}+{58}^2}+\frac{{0.0016}^2}{8{\pi }^2}\ln \left(58+\sqrt{\frac{{0.0016}^2}{4{\pi }^2}+{58}^2}\right)-\\ \frac{1}{2}23\sqrt{\frac{{0.0016}^2}{4{\pi }^2}+{23}^2}-\frac{{0.0016}^2}{8{\pi }^2}\ln \left(23+\sqrt{\frac{{0.0016}^2}{4{\pi }^2}+{23}^2}\right)\end{array}\\ =5566509\text{mm}=\text{5566}\text{.5}\text{m}\end{array}}$

>> syms h r0 N u a;
>> y=int('sqrt(a^2+u^2)',u)
y =(u*(a^2 + u^2)^(1/2))/2 + (a^2*log(u + (a^2 + u^2)^(1/2)))/2
>> yy=subs(y,a,h/(2*pi));
>> s=(subs(yy,u,r0+h*N)-subs(yy,u,r0))*2*pi/h;
>> longitud=subs(s,{r0,h,N},{23,0.0016,21875});
>> double(longitud)/1000
ans =   5.5665e+03

• Cálculo aproximado

Obtenemos una solución aproximada de la integral, si nos damos cuenta que el primer término debajo de la raíz cuadrada h²/(4π²) es muy pequeño en comparación con el segundo.

${\displaystyle \begin{array}{l}s={\displaystyle \underset{0}{\overset{2\pi N}{\int }}\sqrt{\frac{h^2}{4{\pi }^2}+{\left(R_0+\frac{h}{2\pi }\theta \right)}^2}}d\theta \approx {\displaystyle \underset{0}{\overset{2\pi N}{\int }}\left(R_0+\frac{h}{2\pi }\theta \right)}d\theta ={R_0\theta +\frac{h}{4\pi }{\theta }^2|}_0^{2\pi N}=\\ R_{0}2\pi N+\frac{h}{4\pi }{\left(2\pi N\right)}^2=23·2\pi ·21875+\frac{0.0016}{4\pi }{\left(2\pi ·21875\right)}^2=5566509\text{mm}=5566.5\text{m}\end{array}}$

La longitud de la espiral de Arquímedes se puede obtener aún más rápidamente, calculando el radio medio R_m=(R₀+R_f)/2=40.5 mm de las pistas y multiplicando la longitud de la pista media por el número N de pistas considerando que tienen el mismo radio R_m

s=N·2πR_m=5566.5 m

Velocidad angular de rotación

La velocidad de lectura es constante, v=s/T

${\displaystyle v=\frac{5566}{72·60}=1.29\text{m/s}}$

Sin embargo, la velocidad angular de rotación cambia, la velocidad angular inicial es

ω₀=v/R₀=56.0 rad/s y la velocidad angular final es ω_f=v/R_f=22.2 rad/s

La velocidad angular de rotación en función del ángulo θ es

${\displaystyle \omega =\frac{v}{r}\frac{d\theta }{dt}=\frac{v}{r_0+\frac{h}{2\pi }\theta }}$

Integrando

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\theta }{\int }}\left(r_0+\frac{h}{2\pi }\theta \right)}d\theta ={\displaystyle \underset{0}{\overset{t}{\int }}v·dt}\\ \frac{h}{4\pi }{\theta }^2+r_0\theta -vt=0\\ \theta =\frac{2\pi r_0}{h}\left(\sqrt{1+\frac{hvt}{\pi r_0^2}}-1\right)\end{array}}$

En el instante t=72·60=4320 s que se completa la lectura del CD

${\displaystyle \theta =\frac{2\pi ·23}{0.0016}\left(\sqrt{1+\frac{0.0016·1290·4320}{\pi ·{23}^2}}-1\right)=137444.7\text{rad}=\text{21875}\text{vueltas}}$

Derivando con respecto del tiempo obtenemos la expresión de la velocidad angular ω en función del tiempo t.

${\displaystyle \omega =\frac{d\theta }{dt}=\frac{v}{r_0}\frac{1}{\sqrt{1+\frac{hvt}{\pi r_0^2}}}=\frac{{\omega }_0}{\sqrt{1+\frac{{\omega }_{0}ht}{\pi r_0}}}}$

Donde ω₀=v/r₀ es la velocidad angular inicial, para t=0

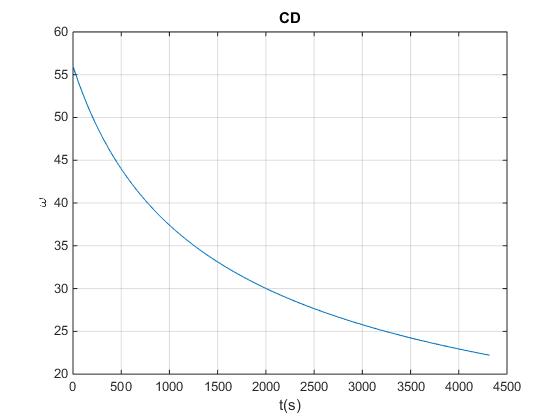
En la figura, se muestra la variación de la velocidad angular ω con el tiempo t.

h=1.6e-6;
R0=23e-3;
w0=56;
w= @(t) w0/sqrt(1+w0*h*t/(pi*R0));
fplot(w,[0,72]*60)
grid on
xlabel('t(s)')
ylabel('\omega')
title('CD')

Referencias

Sawicki M. Angular speed of a compact disc. The Physics Teacher Vol 44, September 2006, pp. 378-38