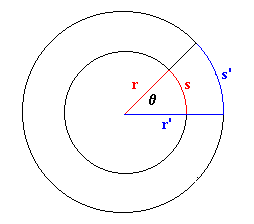
De la definición de radián (unidad natural de medida de ángulos) obtenemos la relación entre el arco y el radio. Como vemos en la figura, el ángulo se obtiene dividiendo la longitud del arco entre su radio

${\displaystyle \theta =\frac{s}{r}=\frac{s\text{'}}{r\text{'}}}$

Velocidad

Derivando s=rθ  respecto del tiempo, obtenemos la relación entre la velocidad lineal y la velocidad angular

${\displaystyle \frac{ds}{dt}=r\frac{d\theta }{dt}v=r\omega }$

La dirección de la velocidad es tangente a la trayectoria circular, es decir, perpendicular a la dirección radial

Aceleración tangencial

Derivando esta última relación con respecto del tiempo obtenemos la relación entre la aceleración tangencial a_t y la aceleración angular.

${\displaystyle \frac{dv}{dt}=r\frac{d\omega }{dt}{a}_t=r\alpha }$

Un móvil tiene aceleración tangencial, siempre que el módulo de su velocidad cambie con el tiempo.

Aceleración normal

El cálculo de la componente normal de la aceleración es algo más complicado. La aceleración normal está relacionada con el cambio de la dirección de la velocidad con el tiempo.

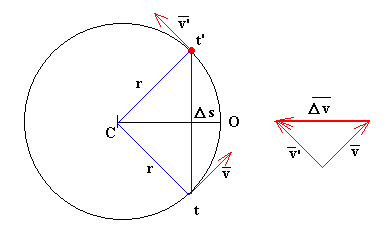
Supongamos un móvil que describe un movimiento circular uniforme.

• En el instante t la velocidad del móvil es $\overrightarrow{v}$ , cuyo módulo es v, y cuya dirección es tangente a la circunferencia.
• En el instante t' la velocidad del móvil $\overrightarrow{v\text{'}}$ , que tiene el mismo módulo v, pero su dirección ha cambiado.

Calculemos el cambio de velocidad $\overrightarrow{\Delta v}=\overrightarrow{v\text{'}}-\overrightarrow{v}$ que experimenta el móvil entre los instantes t y t', tal como se ve en la figura. El vector $\overrightarrow{\Delta v}$ tiene dirección radial y sentido hacia el centro de la circunferencia. Los triángulos de color rojo y de color azul de la figura son isósceles y semejantes por lo que establecemos la siguiente relación

${\displaystyle \frac{\Delta s}{r}=\frac{\Delta v}{v}}$

Donde la cuerda Δs es el módulo del vector desplazamiento entre los instantes t y t'

Dividiendo ambos miembros entre el intervalo de tiempo Δt=t'-t

${\displaystyle \frac{\Delta v}{\Delta t}=\frac{v}{r}\frac{\Delta s}{\Delta t}}$

Cuando el intervalo de tiempo Δt tiende a cero, la cuerda Δs se aproxima al arco, y el cociente ds/dt nos da el módulo de la velocidad v del móvil,

${\displaystyle a_n=\underset{\Delta t\to 0}{\lim }\frac{\Delta v}{\Delta t}=\frac{v}{r}\underset{\Delta t\to 0}{\lim }\frac{\Delta s}{\Delta t}=\frac{v}{r}\frac{ds}{dt}}$

La aceleración normal a_n tiene dirección radial y sentido hacia el centro de la circunferencia que describe el móvil y su módulo viene dado por una u otra de las expresiones siguientes:

${\displaystyle a_n=\frac{v^2}{r}={\omega }^{2}r}$

Esta es la deducción más elemental de la fórmula de la aceleración normal que se basa en la identificación de la longitud del arco entre dos puntos de la circunferencia con la cuerda que pasa por dichos puntos, cuando ambos puntos están muy próximos entre sí.

Resumen

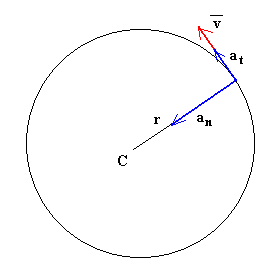
La dirección de la velocidad de un móvil en movimiento circular es tangente a la circunferencia que describe.

Un móvil tiene aceleración tangencial a_t siempre que cambie el módulo de la velocidad con el tiempo. El sentido de la aceleración tangencial es el mismo que el de la velocidad si el móvil acelera y es de sentido contrario, si se frena. Un móvil que describe un movimiento circular uniforme no tiene aceleración tangencial.

Un móvil que describe un movimiento circular siempre tiene aceleración normal, a_n ya que cambia la dirección de la velocidad con el tiempo. La aceleración normal tiene dirección radial y sentido hacia el centro de la circunferencia que describe.

La aceleración del móvil se obtiene sumando vectorialmente ambas componentes de la aceleración.

Ejemplo

Una rueda de r=0.1 m de radio está girando con una velocidad de ω₀=4π rad/s, se le aplican los frenos y se detiene en 4s. Calcular

• La aceleración angular

  ω=ω₀+αt

  En el instante t=4 s la velocidad angular ω=0

  α=-π rad/s²

• El ángulo girado hasta este instante es

  ${\displaystyle \begin{array}{l}\theta ={\theta }_0+{\omega }_{0}t+\frac{1}{2}\alpha t^2\\ \theta =0+4\pi ·4+\frac{1}{2}(-\pi )4^2=8\pi \text{rad}\end{array}}$



• En el instante t=1 s, la posición y la velocidad angular del móvil es

  θ=7π/2=2π+3π/2 rad

  ω=4π+(-π)·1=3π rad/s

• La velocidad lineal

  v=ω·r     v=0.3π m/s

• La componente tangencial de la aceleración es

  a_t=α·r      a_t=-0.1π m/s²

• La componente normal de la aceleración es

  a_n=v²/r    a_n=0.9π² m/s²

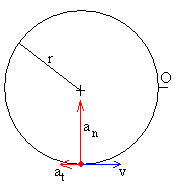
Movimiento de un saltador sobre una plataforma que gira con velocidad angular constante.

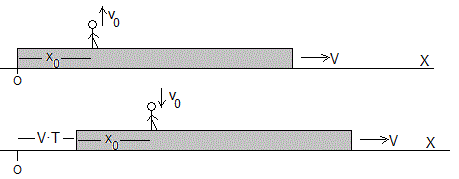
Supongamos una plataforma que se mueve a lo largo del eje X con velocidad constante V. Una persona salta verticalmente sobre la plataforma en una determinada posición x₀ y cae en la misma posición

Si v₀ es la velocidad inicial del saltador, el tiempo T que tarda en regresar a la plataforma es T=2v₀/g.

Desde el punto de vista del observador sobre la plataforma, el saltador parte de la posición x₀ y regresa a la misma posición. Para el observador en tierra, el saltador parte de la posición x₀ y regresa a la posición x₀+VT

Vamos a analizar ahora, que sucede en una plataforma en rotación con velocidad angular ω constante.

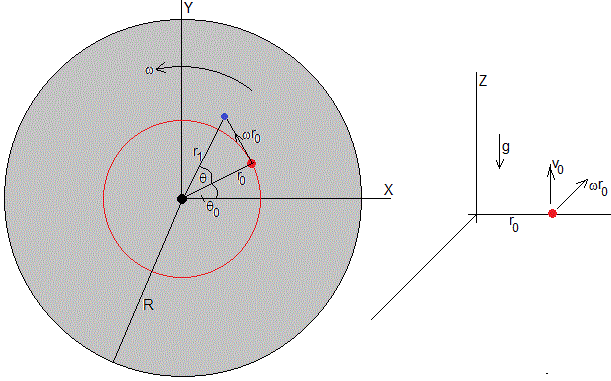
Desde el punto de vista del observador en tierra, el saltador está situado inicialmente a una distancia r₀ del eje de la plataforma giratoria haciendo un ángulo inicial θ₀ con el eje X.

La velocidad del saltador es ωr₀, cuya dirección es tangente a la circunferencia de radio r₀. Una vez iniciado el salto, en el instante t=0, el saltador se mueve horizontalmente con esta velocidad y verticalmente, con velocidad v₀-gt.

Después de un tiempo T=2v₀/g regresa a la plataforma, a una distancia r₁ del eje, haciendo un ángulo θ₀+θ con el eje X, tal como se aprecia en la figura.

θ₀ es el ángulo inicial de partida y θ es el ángulo entre las posiciones inicial y final del salto

${\displaystyle \tan \theta =\frac{\omega r_{0}T}{r_0},\tan \theta =\omega T}$

que es independiente del radio r, es constante para todos los saltos

La hipotenusa del triángulo rectángulo es

${\displaystyle r_1=\sqrt{r_0^2+{\left(\omega r_{0}T\right)}^2}=r_0\sqrt{1+{\left(\omega T\right)}^2}}$

Supongamos que el saltador una vez que impacta sobre la plataforma vuelve a saltar una y otra vez sin descanso. Al cabo de un número de n de saltos, se habrá caído de la plataforma de radio R.

• Al terminar el segundo salto, en el instante 2T, el saltador se encontrará sobre la plataforma a una distancia r₂ del eje haciendo un ángulo θ₀+2θ

${\displaystyle r_2=r_1\sqrt{1+{\left(\omega T\right)}^2}=r_0\left(1+{\left(\omega T\right)}^2\right)}$

• Al terminar el tercer salto, en el instante 3T, el saltador se encontrará sobre la plataforma a una distancia r₃ del eje haciendo un ángulo θ₀+3θ

${\displaystyle r_3=r_2\sqrt{1+{\left(\omega T\right)}^2}=r_0{\left(1+{\left(\omega T\right)}^2\right)}^{3/2}}$

• Al terminar el salto k, en el instante kT, el saltador se encontrará sobre la plataforma a una distancia r_k del eje haciendo un ángulo θ₀+k·θ

${\displaystyle r_k=r_0{\left(1+{\left(\omega T\right)}^2\right)}^{k/2}}$



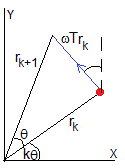
Suponiendo que el saltador parte del eje X, θ₀=0, el saltador inicia el salto k+1 en el punto de coordenadas polares (r_k, k·θ)

${\displaystyle \{\begin{array}{l}{x}_k=r_k\cos \left(k\theta \right)\\ y_k=r_k\sin \left(k\theta \right)\end{array}}$

El movimiento posterior se realiza a lo largo de la tangente a la circunferencia de radio r_k con velocidad ω·r_k, las coordenadas en el plano horizontal del saltador mientras se encuentra suspendido en el aire, serán

${\displaystyle \{\begin{array}{l}x=r_k\cos \left(k\theta \right)-\left(\omega r_k\right)\sin \left(k\theta \right)\left(t-kT)\right)\\ y=r_k\sin \left(k\theta \right)+\left(\omega r_k\right)\cos \left(k\theta \right)\left(t-kT)\right)\end{array}}$

En el instante t=(k+1)T, el saltador regresa a la plataforma y finaliza el salto k+1. Las coordenadas del punto de impacto son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{x}_{k+1}=r_k\cos \left(k\theta \right)-\left(\omega r_k\right)\sin \left(k\theta \right)T\\ y_{k+1}=r_k\sin \left(k\theta \right)+\left(\omega r_k\right)\cos \left(k\theta \right)T\end{array}\\ r_{k+1}=\sqrt{x_{k+1}^2+y_{k+1}^2}=\sqrt{r_k^2+{\left(\omega r_k\right)}^2{T}^2}=r_k\sqrt{1+{\left(\omega T\right)}^2}\end{array}}$

Al terminar el salto n, el saltador se caerá de la plataforma

${\displaystyle r_0{\left(1+{\left(\omega T\right)}^2\right)}^{n/2}\ge R}$

n será el entero mayor que el cociente

${\displaystyle n>2\frac{\ln R-\ln r_0}{\ln \left(1+{\left(\omega T\right)}^2\right)}}$

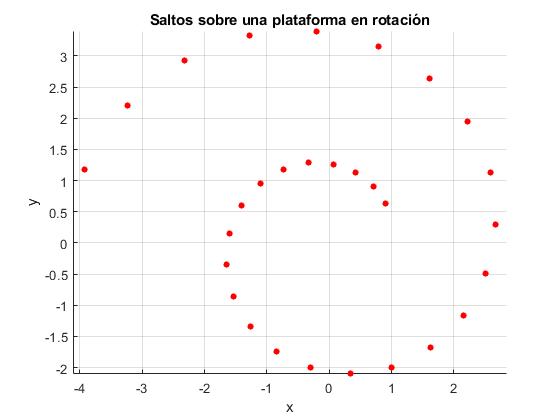
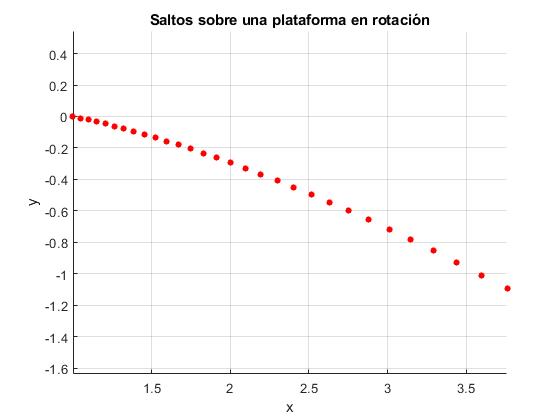
Representamos las posiciones iniciales de cada uno de los saltos hasta que cae de la plataforma, con los siguientes datos:

• Radio de la plataforma, R=4 m
• Velocidad angular de rotación, ω= 3 rpm
• Distancia inicial del saltador al eje de rotación, r₀= 1 m
• Tiempo de salto, mientras el saltador está suspendio en el aire, T= 1 s

R=4; %radio de la plataforma
T=1; %tiempo del salto
r0=1; %distancia inicial al eje de rotación
w=3*2*pi/60; %velocidad angular de rotación
th=atan(w*T);
n=floor(2*(log(R)-log(r0))/log(1+(w*T)^2)); %número de saltos
hold on
for k=0:n
    r=r0*(1+(w*T)^2)^(k/2); %distancia al eje de rotación
    x=r*cos(k*th); %coordenadas
    y=r*sin(k*th);
    plot(x,y,'ro','markersize',4,'markerfacecolor','r')
end
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Saltos sobre una plataforma en rotación')

Observador sobre la plataforma

Al terminar el salto k, en el instante kT, el saltador se encontrará sobre la plataforma a una distancia r_k del eje haciendo un ángulo k·θ con el eje X, mientras tanto la plataforma habrá girado un ángulo k·ωT. La posición relativa del punto de impacto respecto de la plataforma será

${\displaystyle \{\begin{array}{l}{x}_k=r_k\cos \left(k\theta -k\omega T\right)\\ y_k=r_k\sin \left(k\theta -k\omega T\right)\end{array}}$

Representamos las posiciones de impacto (x_k, y_k) vistas por un observador ligado a la plataforma

R=4; %radio de la plataforma
T=1; %tiempo del salto
r0=1; %distancia inicial al eje de rotación
w=3*2*pi/60; %velocidad angular de rotación
th=atan(w*T);
n=floor(2*(log(R)-log(r0))/log(1+(w*T)^2)); %número de saltos
hold on
for k=0:n
    r=r0*(1+(w*T)^2)^(k/2); %distancia al eje de rotación
    x=r*cos(k*(th-w*T));
    y=r*sin(k*(th-w*T));
    plot(x,y,'ro','markersize',4,'markerfacecolor','r')
end
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Saltos sobre una plataforma en rotación')

El saltador no se mueve en la dirección radial

Actividades

Se introduce

• La velocidad angular ω de la plataforma en rpm, en el control titulado Velocidad angular
• El tiempo T del salto, mientras el saltador se encuentra suspendido en el aire, en el control titulado Tiempo suspendido
• Se ha fijado el radio de la plataforma, R=4 m
• Se ha fijado la distancia inicial del saltador al eje de rotación, r₀= 1 m

Se pulsa el botón titulado Nuevo

En la parte superior izquierda, se proporcionan los datos de

• El tiempo, t en s
• Las distancias al eje de rotación, r_k en m
• El número de saltos completos

Los puntos de color rojo indican las posiciones de partida del saltador sobre la plataforma. El punto de color azul, muestra al saltador suspendido en el aire, mientas efectúa el salto. Una flecha señala la dirección de la velocidad horizontal del saltador, perpendicular a la dirección radial en el momento en el que se inicia el salto

Referencias

Terrence Toepker. Jumping Off a Merry-Go-Round. The Physics Teacher. Vol. 60, March 2022. pp. 176-178