Velocidad en un instante

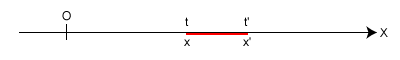
Supongamos ahora que en el tiempo t, el móvil se encuentra en posición x, más tarde, en el instante t' el móvil se encontrará en la posición x'. Decimos que móvil se ha desplazado Δx=x'-x en el intervalo de tiempo Δt=t'-t, medido desde el instante t al instante t'.

La velocidad media entre los instantes t y t' está definida por

${\displaystyle <v>=\frac{x\text{'}-x}{t\text{'}-t}=\frac{\Delta x}{\Delta t}}$

Para determinar la velocidad en el instante t, debemos hacer el intervalo de tiempo Δt tan pequeño como sea posible, en el límite cuando Δt tiende a cero.

Una partícula se mueve a lo largo del eje X, de manera que su posición en cualquier instante t está dada por x=5·t²+1, donde x se expresa en metros y t en segundos.

Calcular su velocidad promedio en el intervalo de tiempo entre:

• 2 y 3 s.
• 2 y 2.1 s.
• 2 y 2.01 s.
• 2 y 2.001 s.
• 2 y 2.0001 s.
• Calcula la velocidad en el instante t=2 s.

Como apreciamos en la tabla, cuando el intervalo Δt→0, la velocidad media tiende a 20 m/s. La velocidad en el instante t=2 s es una velocidad media calculada en un intervalo de tiempo que tiende a cero.

>> format long
>> t0=2;
>> x0=5*t0^2+1;
>> t=t0+1./10.^(0:5);
>> x=5*t.^2+1;
>> vm=(x-x0)./(t-t0)
vm =
  25.000000000000000  
  20.499999999999989  
  20.049999999999883  
  20.004999999999811  
  20.000499999988079  
  20.000050000004137

Ahora, calculamos la velocidad en cualquier instante t

• La posición del móvil en el instante t es x=5t²+1
• La posición del móvil en el instante t+Δt es  x'=5(t+Δt)²+1=5t²+10tΔt+5Δt²+1
• El desplazamiento es Δx=x'-x=10tΔt+5Δt²
• La velocidad media <v> es

${\displaystyle <v>=\frac{10t·\Delta t+5·\Delta t^2}{\Delta t}=10t+5·\Delta t}$

La velocidad en el instante t es el límite de la velocidad media cuando el intervalo de tiempo tiende a cero

${\displaystyle v=\underset{\Delta t\to 0}{\lim }<v>=\underset{\Delta \mathrm{<mtext>\hspace{0.17em}</mtext>t}\to 0}{\lim }\left(10t+5\Delta t\right)=10t\text{m/s}}$

La velocidad en un instante t se calcula directamente, hallando la derivada de la posición x respecto del tiempo.

${\displaystyle \begin{array}{l}x=5t^2+1\text{m}\\ v=\frac{dx}{dt}=10t\text{m/s}\end{array}}$

En el instante t=2 s, v=20 m/s

Desplazamiento de un móvil

Dada la velocidad del móvil en función del tiempo, vamos a calcular el desplazamiento del móvil entre los instantes t₀ y t.  En los casos en los que la velocidad es constante o varía linealmente con el tiempo, el desplazamiento se calcula fácilmente

1. Si v=35 m/s, el desplazamiento del móvil entre los instantes t₀=0 y t=10 s es Δx=35·10=350 m



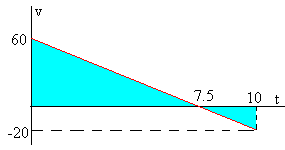
2. Si v=-8·t+60. el desplazamiento del móvil entre los instantes t₀=0 y t=10 s es la suma de las áreas de dos triángulos:

   • el de la izquierda tiene un área de (7.5·60)/2=225 
   • el de la derecha tiene un área de (-20·2.5)/2=-25.

   El desplazamiento es el área total Δx=225+(-25)=200 m

3. En otros casos, calculamos el desplazamiento aproximado, siguiendo el procedimiento que se muestra en la figura



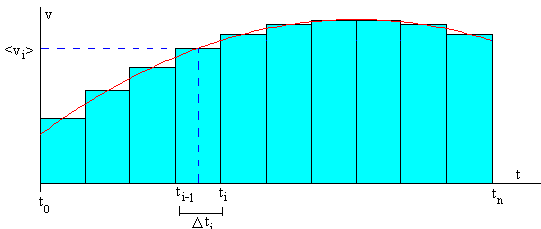
En el instante t_i-1 la velocidad del móvil es v_i-1, en el instante t_i la velocidad del móvil es v_i. La velocidad media <v_i> en el intervalo de tiempo Δt_i=t_i-t_i-1 comprendido entre t_i-1 y t_i es

${\displaystyle <v_i>=\frac{v(t_i)+v(t_{i-1})}{2}}$

El desplazamiento del móvil durante el intervalo de tiempo Δt_i=t_i-t_i-1 comprendido entre t_i-1 y t_i es aproximadamente el área del rectángulo <v_i>·Δt_i. El desplazamiento total x-x₀ entre el instante inicial t₀, y el instante final t=t_n es, aproximadamente

${\displaystyle x-x_0\approx \sum _{i=1}^n<v_i>\Delta t_i}$

donde n es el número de intervalos

Si v=-t²+14t+21 (m/s) y tomamos n=10 intervalos iguales, entre los instantes t₀=0 y t=10 s el desplazamiento aproximado vale

x-x₀≈(27.7+39.8+49.8+57.7+63.7+67.7+69.7+69.8+67.8+63.8)·1=577.5 m

n=10;  %divisiones, cambiar a 20
t=linspace(0,10,n+1);
tt=t+10/(2*n);
tt=tt(1:end-1);
v=-tt.^2+14*tt+21;
area=sum(v)*10/n;  %area de los rectángulos
hold on
bar(tt,v,1,'c')

%representación gráfica de la función v(t)
t=linspace(0,10,100);
v=-t.^2+14*t+21;
plot(t,v,'r')
text(0.25,60,num2str(area))
ylim([0 max(v)+5])
xlim([-0.5,10.5])
title('Integral definida')
xlabel('t')
ylabel('v')
hold off	



4. Cuando el número de intervalos en los que se ha dividido un intervalo dado (t₀, t) es muy grande. En el límite, Δt_i→0

${\displaystyle x-x_0=\underset{t_0}{\overset{t}{\int }}v·dt}$

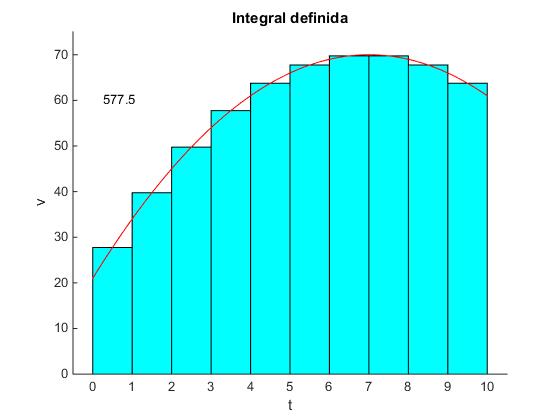
Si v=-t²+14t+21 (m/s), el desplazamiento entre los instantes t₀=0 y t=10 s vale

${\displaystyle x-x_0=\underset{0}{\overset{10}{\int }}(-t^2+14t+21)·dt={-\frac{t^3}{3}+7t^2+21t|}_0^{10}=\frac{1730}{3}\text{m}}$