Usain Bolt batió los records existentes hasta entonces en los Juegos Olímpicos de Pekín de 2008 y en los Campeonatos del Mundo de Berlín de 2009. Los datos correspondientes a este campeonato son los siguientes

Modelo 1

• Aceleración

En el modelo más simple, el movimiento del corredor se describe mediante dos fuerzas: la fuerza que ejerce el corredor F y una fuerza de rozamiento que se opone a su movimiento proporcional a la velocidad v

${\displaystyle m\frac{dv}{dt}=F-\alpha v}$

• Velocidad

Integramos, sabiendo que el corredor está en reposo v=0, en el momento de la salida t=0.

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{v}{\int }}\frac{dv}{\frac{F}{m}-\frac{\alpha }{m}v}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ v=\frac{F}{\alpha }\left(1-\exp \left(-\frac{\alpha t}{m}\right)\right)\end{array}}$

• Posición

Integramos de nuevo, para calcular la posición x en función del tiempo t, sabiendo que parte del origen x=0, en el instante t=0.

${\displaystyle \begin{array}{l}x={\displaystyle \underset{0}{\overset{t}{\int }}\frac{F}{\alpha }\left(1-\exp \left(-\frac{\alpha t}{m}\right)\right)dt}\\ x=\frac{F}{\alpha }t-\frac{Fm}{{\alpha }^2}\left(1-\exp \left(-\frac{\alpha t}{m}\right)\right)\end{array}}$

La posición x depende de dos parámetros a=F/m y b=α/m

${\displaystyle x=\frac{a}{b}t-\frac{a}{b^2}\left(1-\exp \left(-bt\right)\right)}$

Hacemos un ajuste no lineal empleando la función fminsearch de MATLAB. Ajustamos los datos de Bolt a esta función x(t), calculando los valores de los parámetros a y b de ajuste

x=0:10:100; %distancias
t=[0,1.89,2.88,3.78,4.64,5.47,6.29,7.1,7.92,8.75,9.58]; %tiempos
hold on
plot(t,x,'ro','markersize',4,'markerfacecolor','r')
% a(1) es a, a(2) es b
f=@(a,t) a(1)*t/a(2)-a(1)*(1-exp(-t*a(2)))/a(2)^2;      
error=@(a) sum((x-f(a,t)).^2);
a0=[1,8];  %valor inicial
af=fminsearch(error,a0);
g=@(t) f(af,t);
fplot(g,[t(1),t(end)])
title('Posición. Modelo 1')
xlabel('t')
ylabel('x')
grid on
hold off 

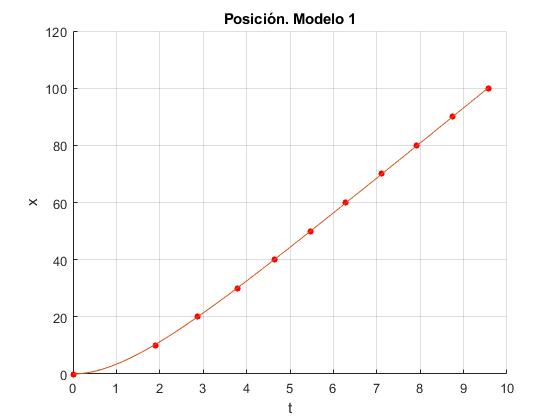
>> af
af =    8.4910    0.6885

Los valores de los parámetros son a=8.4910 m/s² y b=0.6885 s^-1

Conocidos los valores de los parámetros representamos la velocidad del corredor en función del tiempo

${\displaystyle v=\frac{a}{b}\left(1-e^{-bt}\right)}$

a=8.4910; %parámetros
b=0.6885;
fplot(@(t) a*(1-exp(-b*t))/b ,[0,9.58])
title('Velocidad, modelo 1')
xlabel('t')
ylabel('v')
ylim([0,13])
grid on

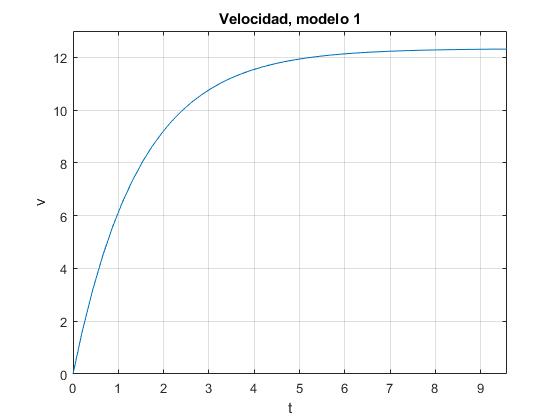
La velocidad crece rápidamente hasta que adquiere un valor casi constante, la velocidad final en el instante t=9.58 s es v=12.32 m/s

Modelo 2

No parece que sea una situación realista considerar que la fuerza F que ejerce el corredor se mantenga constante, por lo que se propone una fuerza F(t)=F-βt, que disminuye linealmente con el tiempo

• Aceleración

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=\left(F-\beta t\right)-\alpha v\\ \frac{dv}{dt}+\frac{\alpha }{m}v=\frac{F}{m}-\frac{\beta }{m}t\end{array}}$

• Velocidad

La solución de la ecuación diferencial homogénea es v=Aexp(-αt/m). La solución particular es v₁=Bt+C. Introducimos la solución particular en la ecuación diferencial para determinar los coeficientes B y C

${\displaystyle B=-\frac{\beta }{\alpha },C=\frac{F}{\alpha }+\frac{m\beta }{{\alpha }^2}}$

La solución de la ecuación diferencial es la suma de ambas

${\displaystyle v=A\exp \left(-\frac{\alpha }{m}t\right)-\frac{\beta }{\alpha }t+\frac{F}{\alpha }+\frac{m\beta }{{\alpha }^2}}$

Determinamos el coeficente A, sabiendo que el corredor está en reposo v=0, en el momento de la salida t=0.

${\displaystyle v=\left(\frac{F}{\alpha }+\frac{m\beta }{{\alpha }^2}\right)\left(1-\exp \left(-\frac{\alpha }{m}t\right)\right)-\frac{\beta }{\alpha }t}$

La velocidad depende de tres parámetros a, b y c

${\displaystyle v=a\left(1-e^{-ct}\right)-bt}$

• Posición

Integramos de nuevo, para calcular la posición x en función del tiempo t, sabiendo que parte del origen x=0, en el instante t=0.

${\displaystyle \begin{array}{l}x={\displaystyle \underset{0}{\overset{t}{\int }}\left(a\left(1-e^{-ct}\right)-bt\right)dt}\\ x=at-\frac{b}{2}{t}^2-\frac{a}{c}\left(1-e^{-ct}\right)\end{array}}$

Ajustamos los datos de Bolt a esta función x(t), calculando los valores de los parámetros a, b y c de ajuste

x=0:10:100; %distancia
t=[0,1.89,2.88,3.78,4.64,5.47,6.29,7.1,7.92,8.75,9.58];
hold on
plot(t,x,'ro','markersize',4,'markerfacecolor','r')
% a(1) es a, a(2) es b y a(3) es c
f=@(a,t) a(1)*t-a(2)*t.^2/2-a(1)*(1-exp(-t*a(3)))/a(3);      
error=@(a) sum((x-f(a,t)).^2);
a0=[10,0.1,1];  %valor inicial
af=fminsearch(error,a0);
g=@(t) f(af,t);
fplot(g,[t(1),t(end)])
title('Posición, modelo 2')
xlabel('t')
ylabel('x')
grid on
hold off 

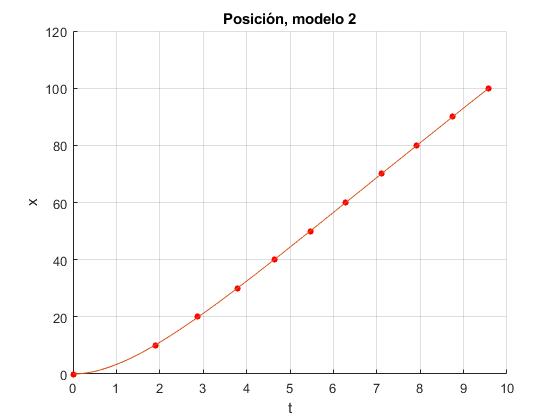
>> af
af =   13.3110    0.1318    0.6189

Los valores de los parámetros son a=13.3110 m/s, b=0.1318 m/s² y c=0.6189 s^-1

Conocidos los valores de los parámetros representamos la velocidad del corredor en función del tiempo

a=13.3110; %parámetros
b=0.1318;
c=0.6189;
fplot(@(t) a*(1-exp(-c*t))-b*t ,[0,9.58])
title('Velocidad, modelo 2')
xlabel('t')
ylabel('v')
ylim([0,13])
grid on

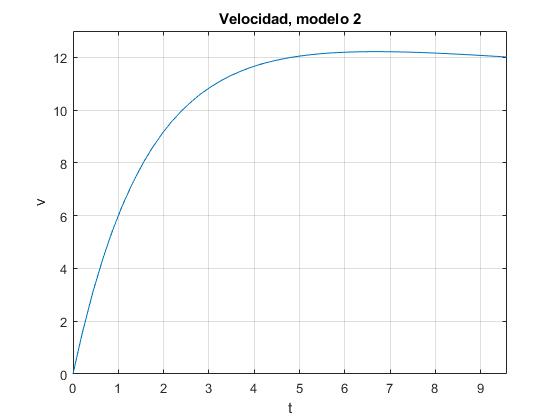
La velocidad crece rápidamente, se mantiene casi constante y luego disminuye ligeramente hacia el final del recorrido. La velocidad final en el instante t=9.58 s es v=12.01 m/s, un poco más pequeña que la predicha por el modelo anterior.

Potencia

La fórmula de la potencia es

${\displaystyle P(t)=m\frac{dv}{dt}v+\left(\frac{C_d\rho A}{2}{\left(v-v_v\right)}^2\right)v+200}$

Los términos que intervienen son:

• v es la velocidad del corredor
• m es la masa del corredor, 86 kg
• v_v es la velocidad del viento, 0.9 m/s
• C_d es el coeficiente de arrastre, 0.5
• A es el área de la sección del corredor, 1 m²
• ρ es la densidad del aire, 1.2 kg/m³
• 200 es la potencia que consume el corredor en el movimiento vertical del centro de masas

Teniendo el cuenta la definición de los parámetros a, b y c

${\displaystyle a=\frac{F}{\alpha }+\frac{m\beta }{{\alpha }^2},b=\frac{\beta }{\alpha },c=\frac{\alpha }{m}}$

La aceleración se expresa

${\displaystyle \begin{array}{l}\frac{dv}{dt}=\frac{F}{m}-\frac{\beta }{m}t-\frac{\alpha }{m}v\\ \frac{dv}{dt}=(ac-b)-cbt-cv\end{array}}$

La fórmula de la potencia P(t) es

${\displaystyle P(t)=m\left(ac-b-cbt-cv\right)v+\left(\frac{C_d\rho A}{2}{\left(v-v_v\right)}^2\right)v+200}$

Donde, la expresión de la velocidad v deducida anteriormente es

${\displaystyle v=a\left(1-e^{-ct}\right)-bt}$

Representamos la función P(t)

a=13.3110; %parámetros
b=0.1318;
c=0.6189;
m=86; %masa
Cd=0.5; %coeficiente de arrastre
rho=1.2; %densidad del aire
vv=0.9; %velocidad del viento
A=1; %ára de la sección transversal del corredor
v=@(t) a*(1-exp(-c*t))-b*t;
f=@(t) m*((a*c-b)-c*b*t-c*v(t)).*v(t)+Cd*rho*A*((v(t)-vv).^2).*v(t)/2+200;
fplot(f ,[0,9.58])
title('Potencia, modelo 2')
ylim([0,2800])
xlabel('t')
ylabel('P')
grid on

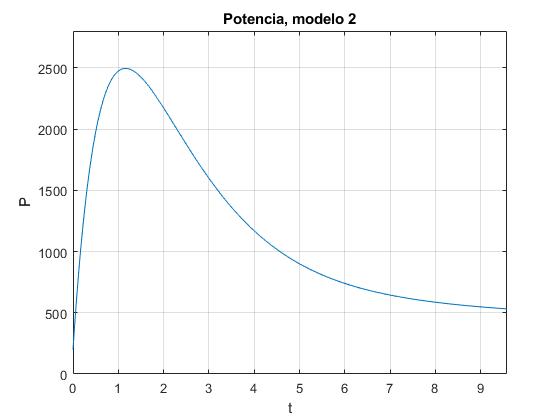
La potencia máxima es 2494 W. El área bajo la curva es la energía consumida, se calcula utilizando el procedimiento numérico trapz de MATLAB

>> t=linspace(0,9.58,100);
>> pot=f(t);
>> energia=trapz(t,pot)
energia =   1.1414e+04

La energía consumida es 11 414 J

Modelo 3

En este apartado, se describe un modelo exponencial para la aceleración

• Aceleración

El modelo cinemático consiste en suponer que la aceleración del corredor es máxima a la salida a₀ y luego, disminuye exponencialmente con el tiempo

${\displaystyle a=a_0{e}^{-t/\tau }}$

• Velocidad

Integramos para obtener la velocidad v del corredor en función del tiempo t. El corredor inicia la carrera en reposo v=0, en el instante t=0

${\displaystyle v={\displaystyle \underset{0}{\overset{t}{\int }}{a}_0{e}^{-t/\tau }·dt=}{a}_0\tau \left(1-e^{-t/\tau }\right)}$

• Posición

Integramos de nuevo, para obtener la posición x del corredor sobre la pista en función del tiempo, la posición de salida es x=0

${\displaystyle x={\displaystyle \underset{0}{\overset{t}{\int }}{a}_0\tau \left(1-e^{-t/\tau }\right)·dt=}{a}_0\tau \left(t+\tau e^{-t/\tau }\right)-a_0{\tau }^2=a_0\tau t-a_0{\tau }^2\left(1-e^{-t/\tau }\right)}$

Ajustamos los datos de Bolt a esta función x=x(t), calculando los valores de los parámetros a₀ y τ de ajuste

x=0:10:100; %distancia
t=[0,1.89,2.88,3.78,4.64,5.47,6.29,7.1,7.92,8.75,9.58];
hold on
plot(t,x,'ro','markersize',4,'markerfacecolor','r')
% a(1) es tau, a(2) es a0
f=@(a,t) a(1)*a(2)*t-a(1)^2*a(2)*(1-exp(-t/a(1)));      
error=@(a) sum((x-f(a,t)).^2);
a0=[1,8];  %valor inicial
af=fminsearch(error,a0);
g=@(t) f(af,t);
fplot(g,[t(1),t(end)])
title('Posición. Modelo 3')
xlabel('t')
ylabel('x')
grid on
hold off 

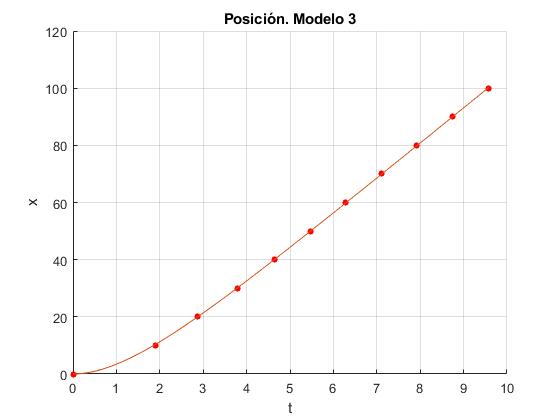
>> af
af =    1.4524    8.4909

Para el corredor Usain Bolt, la aceleración inicial a₀=8.4909 m/s² y la constante de tiempo τ=1.4452 s

Velocidad

Conocidos los valores de los parámetros a₀ y τ, representamos las velocidades v de Bolt y Powell en función del tiempo t

tau=1.4452; %parámetros
a0=8.4909;
fplot(@(t) a0*tau*(1-exp(-t/tau)),[0,9.58])
grid on
ylim([0,13])
xlabel('t')
ylabel('v')
title('Velocidad. Modelo 3')

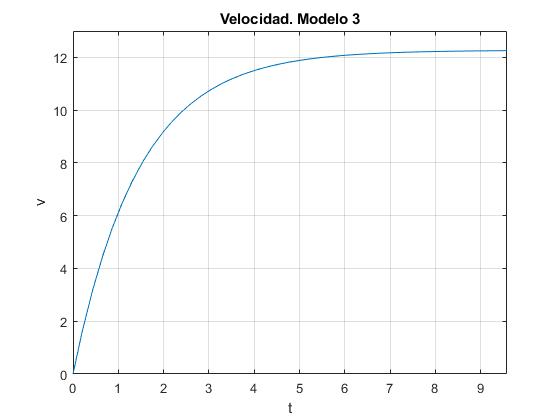
La velocidad crece rápidamente hasta que adquiere un valor casi constante, la velocidad final en el instante t=9.58 s es v=12.25 m/s

Potencia

La potencia P(t) es el producto de la fuerza por la velocidad

${\displaystyle P(t)=\left(m{a}_0{e}^{-t/\tau }\right)\left(a_0\tau \left(1-e^{-t/\tau }\right)\right)=m{a}_0^2\tau ·e^{-t/\tau }\left(1-e^{-t/\tau }\right)}$

Donde m es la masa del corredor. Representamos la potencia por unidad de masa P(t)/m con los parámetros de ajuste a₀=8.4909 m/s² y τ=1.4452 s

tau=1.4452; %parámetros
a0=8.4909;
f=@(t) a0^2*tau*exp(-t/tau).*(1-exp(-t/tau));
fplot(f,[0,9.59])
tm=tau*log(2); %máximo
line([tm,tm],[0,f(tm)],'lineStyle','--','color','k')
grid on
xlabel('t')
ylabel('P(t)/m')
title('Potencia')

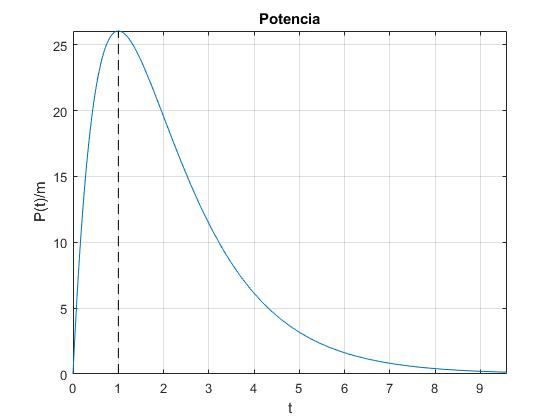
La potencia presenta un máximo que señalamos con la línea a trazos. Calculamos la derivada y la igualamos a cero

${\displaystyle \begin{array}{l}y=e^{-t/\tau }\left(1-e^{-t/\tau }\right)=e^{-t/\tau }-e^{-2t/\tau }\\ \frac{dy}{dt}=-\frac{1}{\tau }{e}^{-t/\tau }+\frac{2}{\tau }{e}^{-2t/\tau }=0\end{array}}$

Llamamos z=e^-t/τ. Llegamos a la ecuación, -z+2z²=0. Cuya raíz positiva es z=1/2, por tanto e^-t/τ=1/2. El máximo se produce para

t=τ·ln2

Referencias

O. Helene, M. T. Yamashita. The force, power, and energy of the 100 meter sprint. Am. J. Phys. 78 (3), March 2010, pp. 307-309

Priyanka deSouza, Vijay A Singh. Simple Models for the 100 Meter Dash. Resonace, June 2012. https://www.ias.ac.in/listing/articles/reso/017/06