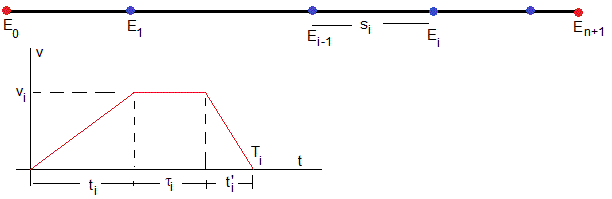
El tren parte de la estación E₀ y llega a la estación E_n+1. En el trayecto hay n estaciones intermedias separadas, s₁, s₂,...s_i,...s_n+1.

El tren parte de la estación E_i-1, incrementa su velocidad con aceleración a_i durante un tiempo t_i alcanzando una velocidad v_i. Se mantiene con velocidad constante durante un tiempo τ_i. Finalmente, disminuye su velocidad con aceleración a'_i hasta que se detiene en la proxima estación E_i empleando para ello un tiempo t'_i. El tren recorre un trayecto de longitud s_i empleando un tiempo T_i=t_i+τ_i+t'_i

${\displaystyle \begin{array}{l}\{\begin{array}{l}{v}_i=a_i{t}_i\\ v_i=\text{cte}\\ 0=v_i-a_i^{\text{'}}{t}_i^{\text{'}}\end{array}\\ s_i=\frac{1}{2}{a}_i{t}_i^2+v_i{\tau }_i+\frac{1}{2}{a}_i^{\text{'}}{t}_i^{\text{'}2}\\ T_i=t_i+{\tau }_i+t_i^{\text{'}}\end{array}}$

La distancia s_i la expresamos, alternativamente

${\displaystyle s_i=\frac{v_i^2}{2}\left(\frac{1}{a_i}+\frac{1}{a_i^{\text{'}}}\right)+v_i{\tau }_i=\frac{v_i^2}{2}{f}_i+v_i{\tau }_i}$

Donde hemos definido una nueva magnitud, f_i=1/a_i+1/a'_i

Conocido s_i y τ_i, tenemos una ecuación de segundo grado en la que despejamos la incógnita v_i

${\displaystyle v_i=\frac{1}{f_i}\left(-{\tau }_i+\sqrt{{\tau }_i^2+2f_i{s}_i}\right)}$

El tiempo T_i que emplea el tren en viajar entre dos estaciones consecutivas es

${\displaystyle T_i=\frac{v_i}{a_i}+{\tau }_i+\frac{v_i}{a_i^{\text{'}}}=v_i{f}_i+{\tau }_i=\sqrt{{\tau }_i^2+2f_i{s}_i}}$

Tiempo mínimo

El tiempo total de viaje es

${\displaystyle T={\displaystyle \sum _{i=1}^{n+1}\sqrt{{\tau }_i^2+2f_i{s}_i}}}$

En este tiempo se excluyen los tiempos de parada en cada una de las estaciones para la subida y bajada de viajeros y mercancías

Queremos que el tiempo total T sea mínimo para una distancia total S entre las estaciones terminales

${\displaystyle S={\displaystyle \sum _{i=1}^{n+1}{s}_i}}$

El método de los multiplicadores de Lagrange nos proporcionan la solución del problema

Tenemos una función T(s_i) y una condición complementaria, la suma de las distancias s_i entre estaciones es el recorrido total S.

Consideramos una nueva función

${\displaystyle \begin{array}{l}F(s_i)=T+\lambda \left(S-{\displaystyle \sum _{i=1}^{n+1}{s}_i}\right)\\ F(s_i)={\displaystyle \sum _{i=1}^{n+1}\sqrt{{\tau }_i^2+2f_i{s}_i}}+\lambda \left(S-{\displaystyle \sum _{i=1}^{n+1}{s}_i}\right)\end{array}}$

Formamos el sistema de ecuaciones

${\displaystyle \begin{array}{l}\frac{\partial F}{\partial s_i}=\mathrm{0,}i=\mathrm{1,2,3...}n+1\\ \frac{f_i}{\sqrt{{\tau }_i^2+2f_i{s}_i}}-\lambda =0\\ 2s_i=\frac{f_i}{{\lambda }^2}-\frac{{\tau }_i^2}{f_i}\end{array}}$

que junto con la condición complementaria determina el parámetro λ

${\displaystyle \begin{array}{l}2S={\displaystyle \sum _{i=1}^{n+1}\frac{f_i}{{\lambda }^2}-\frac{{\tau }_i^2}{f_i}=\frac{1}{{\lambda }^2}\left({\displaystyle \sum _{i=1}^{n+1}{f}_i}\right)}-{\displaystyle \sum _{i=1}^{n+1}\frac{{\tau }_i^2}{f_i}}\\ \frac{1}{{\lambda }^2}=\frac{2S+{\displaystyle \sum _{i=1}^{n+1}\frac{{\tau }_i^2}{f_i}}}{{\displaystyle \sum _{i=1}^{n+1}{f}_i}}\end{array}}$

y los valores s_i de los posibles extremos (máximos o mínimos) condicionados de la función T(s_i)

${\displaystyle s_i=\frac{f_i}{2}\frac{2S+{\displaystyle \sum _{i=1}^{n+1}\frac{{\tau }_i^2}{f_i}}}{{\displaystyle \sum _{i=1}^{n+1}{f}_i}}-\frac{{\tau }_i^2}{2f_i}}$

La suma de las distancias s_i entre estaciones consecutivas nos deberá dar la distancia entre las dos estaciones terminales S

${\displaystyle {\displaystyle \sum _{i=1}^{n+1}{s}_i}=\frac{S{\displaystyle \sum _{i=1}^{n+1}{f}_i}}{{\displaystyle \sum _{i=1}^{n+1}{f}_i}}+\frac{\left({\displaystyle \sum _{i=1}^{n+1}{f}_i}\right)\left({\displaystyle \sum _{i=1}^{n+1}\frac{{\tau }_i^2}{f_i}}\right)}{2{\displaystyle \sum _{i=1}^{n+1}{f}_i}}-\frac{1}{2}\left({\displaystyle \sum _{i=1}^{n+1}\frac{{\tau }_i^2}{f_i}}\right)=S}$

El tiempo T_i que se emplea en recorrrer la distancia s_i entre dos estaciones consecutivas es

${\displaystyle T_i=\sqrt{{\tau }_i^2+2f_i{s}_i}=f_i\sqrt{\frac{2S+{\displaystyle \sum _{i=1}^{n+1}\frac{{\tau }_i^2}{f_i}}}{{\displaystyle \sum _{i=1}^{n+1}{f}_i}}}}$

y el tiempo total T (mínimo) es

${\displaystyle T={\displaystyle \sum _{i=1}^{n+1}{f}_i\sqrt{\frac{2S+{\displaystyle \sum _{i=1}^{n+1}\frac{{\tau }_i^2}{f_i}}}{{\displaystyle \sum _{i=1}^{n+1}{f}_i}}}}=\sqrt{\left({\displaystyle \sum _{i=1}^{n+1}{f}_i}\right)\left(2S+{\displaystyle \sum _{i=1}^{n+1}\frac{{\tau }_i^2}{f_i}}\right)}}$

La velocidad constante v_i que alcanza el tren entre ambas estaciones es

${\displaystyle \begin{array}{l}{T}_i=v_i{f}_i+{\tau }_i\\ v_i=\frac{T_i-{\tau }_i}{f_i}=\sqrt{\frac{2S+{\displaystyle \sum _{i=1}^{n+1}\frac{{\tau }_i^2}{f_i}}}{{\displaystyle \sum _{i=1}^{n+1}{f}_i}}}-\frac{{\tau }_i}{f_i}\end{array}}$

Ejemplo

Consideremos un tres que viaja entre dos ciudades distantes S=250 km, con n=3 estaciones intermedias o bien cuatro tramos de longitud s₁, s₂, s₃ y s₄

Los datos son los siguientes:

Creamos un script para calcular

• Las distancias óptimas s_i entre estaciones consecutivas
• El tiempo mínimo T_i que emplea el tren en recorrer el tramo s_i
• Las velocidades constantes v_i en cada uno de los tramos

tau=[4,6,8,10]/60; %horas
a=[80,120,160,200]; %aceleraciones
ap=[400,480,600,640]; %deceleraciones
f=zeros(1,length(tau));
for i=1:length(f)
    f(i)=1/a(i)+1/ap(i);
end
S=250; %distancia entre las estaciones terminales
cte=(2*S+sum((tau.^2)./f))/sum(f);
T=zeros(1,length(f));
x=zeros(1,length(f));
v=zeros(1,length(f));
for i=1:length(f)
    T(i)=f(i)*sqrt(cte);
    x(i)=f(i)*cte/2-tau(i)^2/(2*f(i));
    v(i)=sqrt(cte)-tau(i)/f(i);
end
disp(T) %tiempos
disp(x) %distancias
disp(v) %velocidad constante

Los resultados son los siguientes

   1.6922    1.1751    0.8931    0.7403
  95.3007   65.8039   49.2530   39.6425
 108.3674  103.2118   95.9697   87.4150

>> sum(x)
ans =   250
>> sum(T)
ans =    4.5007

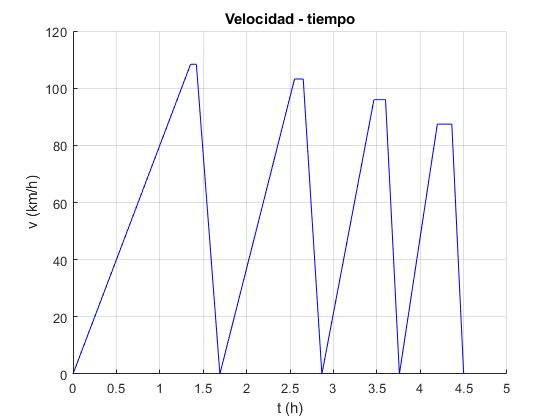
El tiempo total es T=4.5 h empleado en recorrer S=250 km

Añadimos al script este código para representar la velocidad v del tren en función del tiempo t

....
s=zeros(1,length(f)+1);
tt=zeros(1,length(f)+1);
s(1)=0;
tt(1)=0;
for i=2:length(f)+1
    s(i)=s(i-1)+x(i-1);
    tt(i)=tt(i-1)+T(i-1);
end    
%gráfica de la velocidad en función del tiempo
for i=1:length(f)
    line([tt(i), tt(i)+v(i)/a(i)],[0,v(i)],'color','b')
    line([tt(i)+v(i)/a(i),tt(i)+v(i)/a(i)+tau(i)],[v(i),v(i)],'color','b')
    line([tt(i)+v(i)/a(i)+tau(i),tt(i+1)],[v(i),0],'color','b')
end
grid on
xlabel('t (h)')
ylabel('v (km/h)')
title('Velocidad - tiempo')

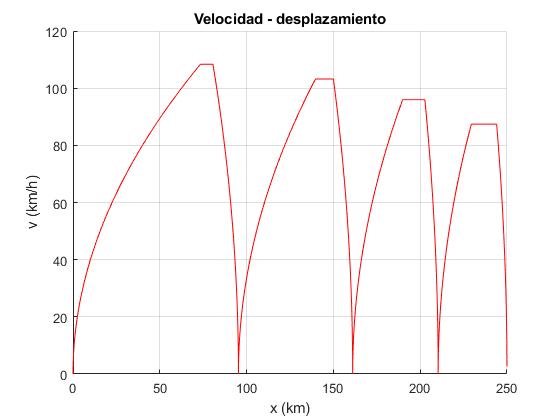
Añadimos al script este código para representar la velocidad v del tren en función del desplazamiento x

....
figure
hold on
for i=1:length(f)
    fplot(@(x) sqrt(2*a(i)*(x-s(i))), [s(i), s(i)+v(i)^2/(2*a(i))],'color','r')
    line([s(i)+v(i)^2/(2*a(i)), s(i)+v(i)^2/(2*a(i))+v(i)*tau(i)],
[v(i),v(i)],'color','r')
    fplot(@(x) sqrt(v(i)^2-2*ap(i)*(x-s(i)-v(i)^2/(2*a(i))-v(i)*tau(i))), 
[s(i)+v(i)^2/(2*a(i))+v(i)*tau(i), s(i+1)],'color','r')
end
hold off
grid on
xlabel('x (km)')
ylabel('v (km/h)')
title('Velocidad - desplazamiento')

Actividades

En este programa interactivo, se observa el movimiento del tren entre las dos estaciones terminales (puntos de color rojo) separadas 250 km. Las estaciones intermedias se se representan por puntos de color azul.

Se traza la gráfica de la velocidad v del tren en función de su desplazamento x a lo largo de la vía, tomando como origen la estación de partida

En la parte superior derecha, se proporcionan los datos de

• El tiempo t en horas
• La posición del tren x en km
• La velocidad del tren v en km/h

Referencias

S N Maitra. A Train Journey between Two Terminating Stations. Resonance – Journal of Science Education, Volume 17, Issue 4, April 2012. https://www.ias.ac.in/listing/articles/reso/017/04