Medida de la velocidad y aceleración

Regresión lineal

Supongamos que estamos midiendo la posición de un móvil en función del tiempo en un movimiento rectilíneo. Si el móvil está libre de fuerzas, esperamos que la relación entre la posición del móvil y el tiempo sea lineal x=x₀+vt. Donde x₀ es la posición del móvil en el instante t=0.

Si medimos las posiciones del móvil x₁ y x₂ en los instantes t₁ y t₂, obtenemos un sistema de dos ecuaciones con dos incógnitas de las que despejamos las cantidades desconocidas x₀ y v. Ahora bien, esta afirmación solamente es cierta en un experimento ideal libre de errores.

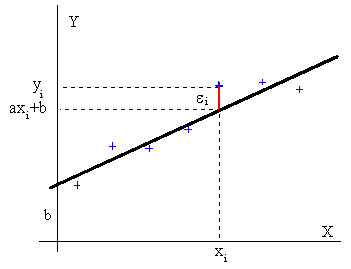
Si efectuamos n medidas de la posición del móvil, el aspecto de la representación gráfica de nuestras medidas será parecido al de la figura más abajo, los puntos de color azul representan los datos experimentales. La relación entre las ordenadas y y las abscisas x de dichos puntos es solamente aproximada, debido a los errores de cada una de las medidas.

Si tomamos únicamente dos puntos para definir la recta el resultado tendría un importante error. Para una mejor estimación de la recta y por tanto, de las magnitudes buscadas, se deberán utilizar las n medidas tomadas.

Supongamos una magnitud física y, relacionada con otra x, mediante la función y=ax+b. Una recta de pendiente a cuya ordenada en el origen es b. Las desviaciones εde los valores de y, véase la figura, serán

ε₁=y₁-(ax₁+b)
ε₂=y₂-(ax₂+b)
...................
ε_i=y_i-(ax_i+b)
...................
ε_n=y_n-(ax_n+b)

Sea E(a,b) la suma de los cuadrados de todas estas desviaciones

E(a,b)=(y₁-ax₁-b)²+(y₂-ax₂-b)²+...(y_i-ax_i-b)²+...+(y_n-ax_n-b)²

$E (a, b) = \sum_{1}^{n} {(y_{i} - a x_{i} - b)}^{2}$

Los valores que minimizan a E(a,b) son aquellos para los que

$\frac{\partial E}{\partial a} = 0 \frac{\partial E}{\partial b} = 0$

Se obtiene así, un sistema de dos ecuaciones con dos incógnitas a y b cuya solución es

$a = \frac{n \sum_{1}^{n} x_{i} y_{i} - (\sum_{1}^{n} x_{i}) (\sum_{1}^{n} y_{i})}{n \sum_{1}^{n} x_{i}^{2} - {(\sum_{1}^{n} x_{i})}^{2}} b = \frac{\sum_{1}^{n} y_{i} - a \sum_{1}^{n} x_{i}}{n}$

Expresiones más elaboradas nos permiten determinar el error de a, Δa y el error de b, Δb

$\begin{array}{l} Δ a = \frac{\sqrt{n} \cdot σ}{\sqrt{n \sum_{1}^{n} x_{i}^{2} - {(\sum_{1}^{n} x_{i})}^{2}}} σ = \sqrt{\frac{\sum_{1}^{n} {(y_{i} - a x_{i} - b)}^{2}}{n - 2}} \\ Δ b = Δ a \cdot \sqrt{\frac{\sum_{1}^{n} x_{i}^{2}}{n}} \end{array}$

La pendiente de la recta se escribirá a±Δa, y la ordenada en el origen b±Δb.

Práctica de laboratorio: Estudio de los movimientos rectilíneos

En el laboratorio disponemos de un carril para estudiar los movimientos rectilíneos: uniforme y uniformemente acelerados, tal como se ve en la fotografía

Movimiento rectilíneo uniforme

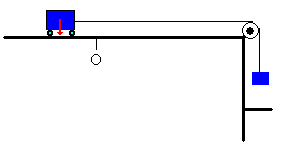
El objetivo de esta práctica, es la medida de la velocidad de un carrito que desliza sin rozamiento a lo largo de un raíl.

Aceleramos el carrito, mediante una cuerda que pasa por una polea situada en el extremo derecho de la regla. Una pesa cuelga de la cuerda. Cuando el carrito pasa por el origen, se deja de acelerar, haciendo que la pesa se detenga sobre un tope. La cuerda deja de actuar sobre el carrito, desde este momento el carrito se mueve con velocidad constante.

Con un reloj medimos el tiempo que tarda el carrito en desplazarse Δx que pueden ser 10,20, 30... cm

Se pulsa el botón titulado Nuevo, el programa genera un número aleatorio que es la velocidad constante del móvil una vez que haya pasado por el origen.

Se establece el desplazamiento del móvil actuando en el control titulado Desplazamiento, se pulsa el botón ►, se mide el tiempo que tarda el móvil en desplazarse (segmento horizontal de color rojo)

Se establece otro desplazamiento, se mide el tiempo y así, sucesivamente

Desplazamiento

Si el carrito se mueve con movimiento rectilíneo y uniforme, su posición x en el instante t es

x=x₀+vt

Poniendo en el eje de las ordenadas las medidas de x y en el eje de abscisas los tiempos t, la pendiente de la recta x=p₁·t+p₂ que mejor ajusta nos dará la medida de la velocidad v=p₁.

Realizamos una experiencia y recogemos los datos que figuran en la tabla.

t(s)	x(cm)
1.9	5
3.8	10
5.7	15
7.6	20
9.5	25
11.4	30
13.3	35
15.2	40
17.1	45

t=[1.9,3.8,5.7,7.6,9.5,11.4,13.3,15.2,17.1];
x=5:5:45;
plot(t,x,'ro','markersize',4,'markerfacecolor','r')
xlabel('t(s)')
ylabel('x(cm)')
title('Movimiento rectilíneo uniforme')
grid on

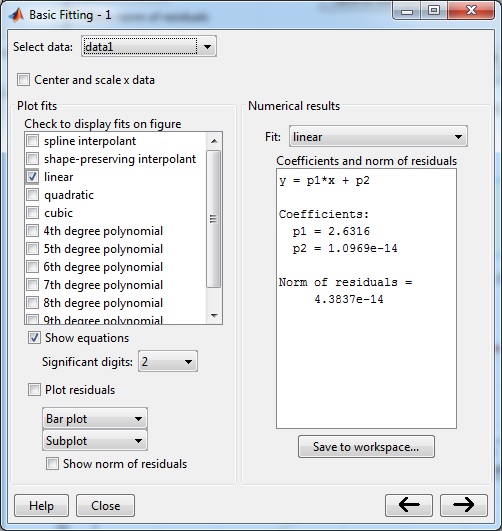
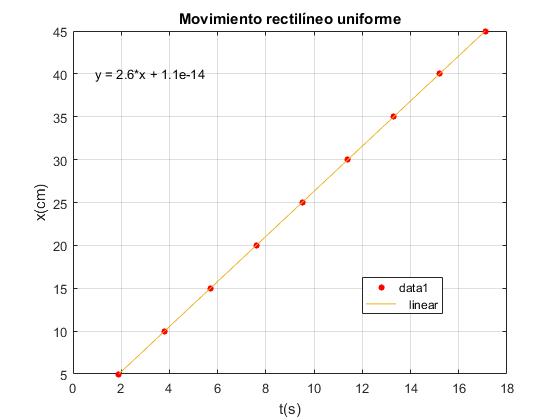
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.

La velocidad v del carrito (pendiente de la recta) es el valor del coeficiente p1. El resultado es v=2.6 cm/s.

La ventana gráfica nos muestra los valores experimentales (puntos de color rojo) y la recta que mejor ajusta.

Movimiento rectilíneo uniformente acelerado

El objetivo de esta práctica, es la medida de la aceleración de un carrito que desliza impulsado por una fuerza constante a lo a lo largo de un raíl.

Aceleramos el carrito, mediante una cuerda que pasa por una polea situada en el extremo derecho de la regla. Una pesa cuelga de la cuerda. El carrito se sitúa en el origen y la fuerza que se ejerce sobre el carrito actúa durante todo su recorrido. El movimiento es uniformemente acelerado.

Con un reloj medimos el tiempo que tarda el carrito en desplazarse Δx que pueden ser 10,20, 30... cm

Se pulsa el botón titulado Nuevo, el programa genera un número aleatorio que es la aceleración constante del móvil.

Se establece otro desplazamiento, se mide el tiempo y así, sucesivamente

Desplazamiento

Si el carrito se mueve con movimiento rectilíneo uniformemente acelerado la su posición x en el instante t es

$x = x_{0} + v_{0} t + \frac{1}{2} a t^{2}$

Poniendo en el eje de las ordenadas las medidas de x y en el eje de abscisas los tiempos t, el coeficiente p₁ polinomio de segundo grado x=p₁·t²+p₂·t+p₃ que mejor ajusta nos dará la mitad del valor de la aceleración p₁=a/2.

Realizamos una experiencia y recogemos los datos que figuran en la tabla.

t(s)	x(cm)
4.7	5
6.6	10
8.0	15
9.3	20
10.5	25
11.5	30
12.4	35
13.3	40
14.1	45

t=[4.7,6.6,8.0,9.3,10.5,11.5,12.4,13.3,14.2];
x=5:5:45;
plot(t,x,'ro','markersize',4,'markerfacecolor','r')
xlabel('t(s)')
ylabel('x(cm)')
title('Movimiento rectilíneo uniformemente acelerado')
grid on

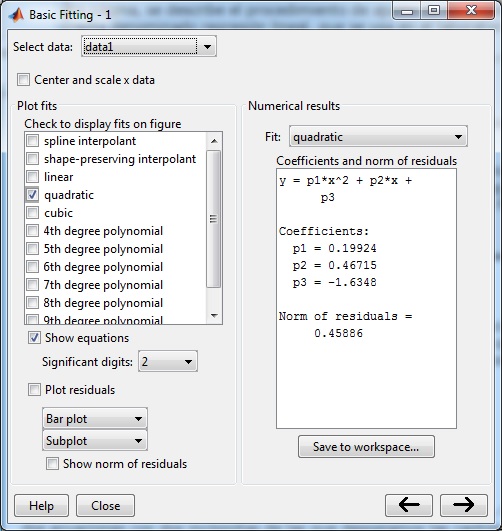
En el menú de la ventana gráfica, seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla quadratic en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 y p3 del polinomio y=p1*x^2 +p2*x+p3 de ajuste.

La acelaración a del carrito es doble el valor del coeficiente p1. El resultado es a=0.4 cm/s².

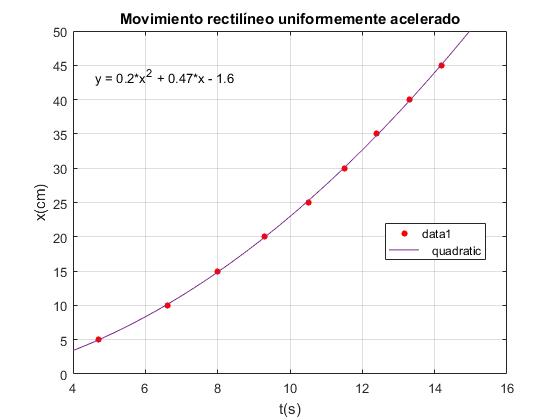
La ventana gráfica nos muestra los valores experimentales (puntos de color rojo) y el polinomio de segundo grado que mejor ajusta.