Una canoa atraviesa un río
Vamos a empezar por un caso particular sencillo
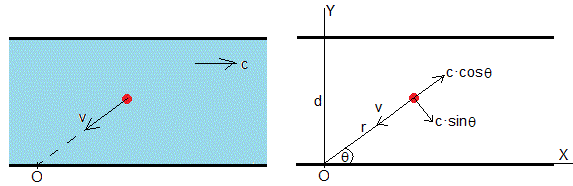
Una canoa se mueve con velocidad constante v sobre el agua de un río cuya corriente se mueve con velocidad constante c, cuya dirección es paralela al eje X. La canoa parte de la posición (0, d), mientras está en movimiento, la dirección de su velocidad apunta hacia el origen O, tal como se muestra en la figura
En un instante t, la distancia del origen a la canoa es r y el ángulo que forma con el eje X es θ
El vector velocidad en coordenadas polares se escribe
Las componentes del vector velocidad y la ecuacion diferencial de la trayectoria, son
Para integrar, efectuamos una separación de variables
Caso particular, la velocidad de la corriente c es igual a la velocidad del bote relativa al agua v
Que es la ecuación de una parábola en coordenadas polares
La constante C se determina sabiendo que la canoa parte de la posición x=0, y=d o bien, r=d y θ=π/2. la constante C=d
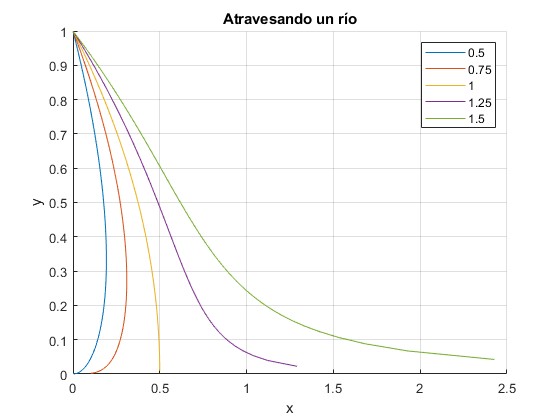
Fijamos la velocidad v=1 de la canoa respecto de la corriente y representamos las trayectorias de una canoa que parte de la posición (1,0), d=1, para distintas velocidades de la corriente c=0.5, 0.75, 1, 1.25, 1.5. Cuando c=1, la trayectoria es una parábola
C=1; %sale de y=1, x=0, es decir, r=1, th=pi/2
th=(0:1:90)*pi/180;
hold on
v=1; %velocidad de la cano sobre el agua
for c=0.5:0.25:1.5
r=C*(tan(th/2)).^(v/c)./sin(th);
plot(r.*cos(th),r.*sin(th),'displayName',num2str(c))
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('y')
title('Atravesando un río')
Problema general
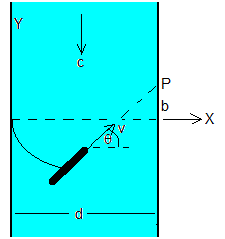
La corriente de anchura d, fluye hacia abajo con velocidad c, y la canoa se mueve con velocidad constante v sobre el agua. Establecemos un sistema de referencia con el origen en el punto de salida de la canoa (x=0, y=0) y los ejes apuntando horizontalmente y verticalmente.
Supongamos que la canoa se mueve sobre el agua apuntando hacia el punto P, de coordenadas (d,b), de modo que la línea que une la canoa con el punto P hace un ángulo θ que va cambiando a medida que la canoa se desplaza. Si la posición de la canoa es (x, y)
En un intervalo de tiempo dt, la canoa se desplaza horizontalmente dx=vcosθ·dt y verticalmente, dy=(vsinθ-c)dt. La ecuación diferencial de la trayectoria de la canoa es
En general, la velocidad c de la corriente dependerá de la coordenada x. Por ejemplo, será más grande en el centro x=d/2 que en las orillas x=0 ó x=d. El perfil de velocidades de la corriente vendrá definido por una función f(x). La ecuación diferencial de la trayectoria de la canoa se escribe
Se resuelve, esta ecuación diferencial con la siguiente condición inicial: la canoa parte del origen, x=0, y=0.
Para integrar la ecuación diferencial se hace siguiente cambio de variable
Obtenemos una ecuación diferencial de variables separadas p y q, que integramos
donde C es una constante de integración que determinaremos a partir de las condiciones iniciales. Nos fijaremos en el primer miembro. Sea z el seno hiperbólico de x, z=sinhx
Llamando y=exp(x), tenemos la ecuación de segundo grado y-1/y=2z, cuyas raíces son
No hay logaritmos de números negativos, la raíz positiva de y es la única válida.
La solución de la ecuación diferencial se reduce a
Deshaciendo los cambios de variable, obtenemos la ecuación de la trayectoria
donde q=log(d-x)
La constante C se determina a partir de la condición inicial x=0, y=0, la canoa parte del origen
Desviación
En la ecuación de la trayectoria sustituimos x=d para calcular la desviación y de la canoa al llegar a la orilla opuesta
Tiempo de viaje
La conoa se desplaza horizontalmente d, con una velocidad variable vcosθ, empleando un tiempo t
Ejemplos
Vamos a considerar distintos perfiles de la velocidad de la corriente f(x)
Velocidad de la corriente constante
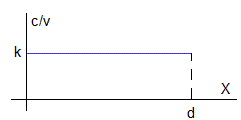
En este caso f(x)=k
La ecuación de la trayectoria es
La constante C1 se determina a partir de las condiciones iniciales, x=0, y=0
Tomamos la raíz positiva de la ecuación de segundo grado en z=dk·C1
Casos particulares
- Para k=1 y b=0, la ecuación de la trayectoria es la parábola
- Para k=1 y b≠0, la ecuación de la trayectoria es una parábola, que alcanza la orilla opuesta desviada
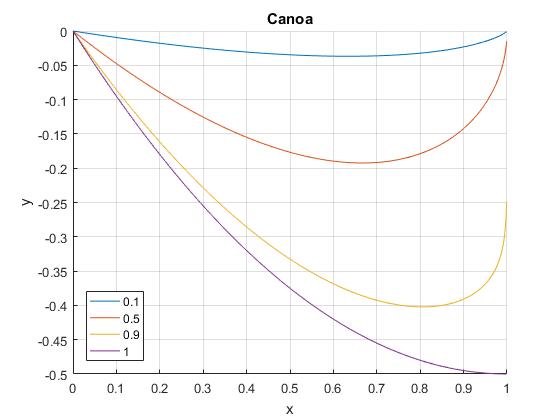
- Para b=0 y k≤1
La canoa que describe esta trayectoria llega a la orilla opuesta x=d y se desvía y=-d/2, en la dirección de la corriente tal como se muestra en la figura
b=0;
d=1;
hold on
for k=[0.1,0.5,0.9,1]
C1=1/d^k;
y=@(x) (d-x).*((d-x).^k*C1-1./((d-x).^k*C1))/2+b;
fplot(y,[0,1],'displayName',num2str(k))
end
hold off
grid on
legend('-DynamicLegend','location','southwest')
xlabel('x')
ylabel('y')
title('Canoa')
Para k<1
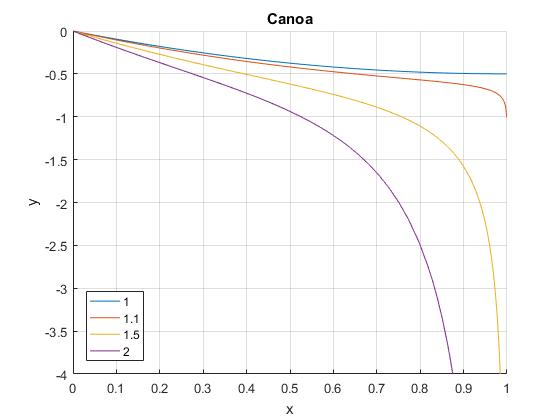
para b=0, dkC1=1
b=0;
d=1;
hold on
for k=[1,1.1,1.5,2]
C1=1/d^k;
y=@(x) (d-x).*((d-x).^k*C1-1./((d-x).^k*C1))/2+b;
fplot(y,[0,1],'displayName',num2str(k))
end
hold off
ylim([-4,0])
grid on
legend('-DynamicLegend','location','southwest')
xlabel('x')
ylabel('y')
title('Canoa')
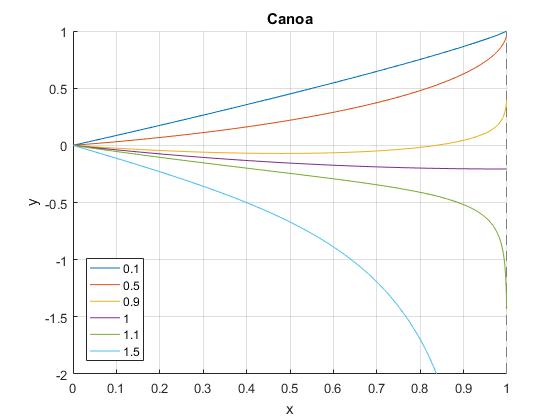
b=1;
d=1;
hold on
for k=[0.1,0.5,0.9,1,1.1,1.5]
C1=(-b/d+sqrt(b^2/d^2+1))/d^k;
y=@(x) (d-x).*((d-x).^k*C1-1./((d-x).^k*C1))/2+b;
fplot(y,[0,1],'displayName',num2str(k))
end
ylim([-2,1])
hold off
grid on
legend('-DynamicLegend','location','southwest')
xlabel('x')
ylabel('y')
title('Canoa')
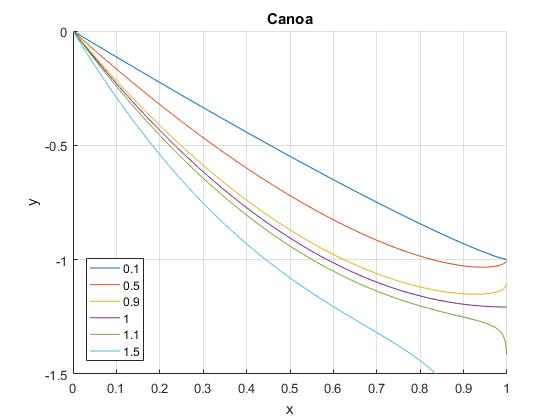
b=-1;
d=1;
hold on
for k=[0.1,0.5,0.9,1,1.1,1.5]
C1=(-b/d+sqrt(b^2/d^2+1))/d^k;
y=@(x) (d-x).*((d-x).^k*C1-1./((d-x).^k*C1))/2+b;
fplot(y,[0,1],'displayName',num2str(k))
end
ylim([-1.5,0])
hold off
grid on
legend('-DynamicLegend','location','southwest')
xlabel('x')
ylabel('y')
title('Canoa')
La velocidad de la corriente se incrementa linealmente
Vamos a considerar el caso de una variación lineal de la velocidad de la corriente. En la orilla x=0, la velocidad c=0 del agua es cero y en la orilla opuesta x=d es c=sv. La función f(x)=sx/d
La ecuación de la trayectoria es
La constante C1 se determina a partir de las condiciones iniciales, x=0, y=0
Tomamos la raíz positiva de la ecuación de segundo grado en z=ds·C1
Como caso particular interesante mencionamos que para s=1 y b=0, la canoa alcanza la orilla opuesta en la posición y=-d/(2e)
b=0;
d=1;
hold on
for s=[0.5,1,1.1,1.5,2]
C1=(-b/d+sqrt(b^2/d^2+1))/d^s;
y=@(x) (d-x).*(C1*((d-x).^s).*exp(s*x/d)-exp(-s*x/d)./((d-x).^s*C1))/2+b;
fplot(y,[0,1],'displayName',num2str(s))
end
ylim([-0.5,0])
hold off
legend('-DynamicLegend','location','southwest')
grid on
xlabel('x')
ylabel('y')
title('Canoa')
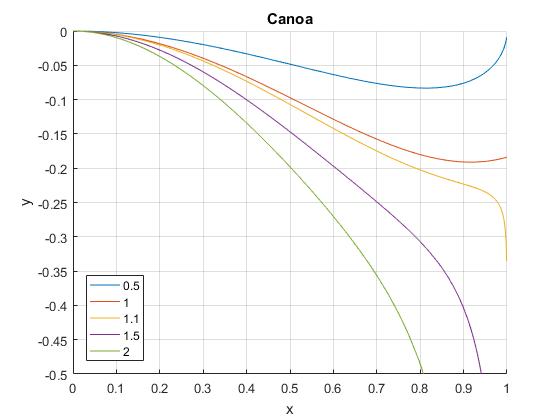
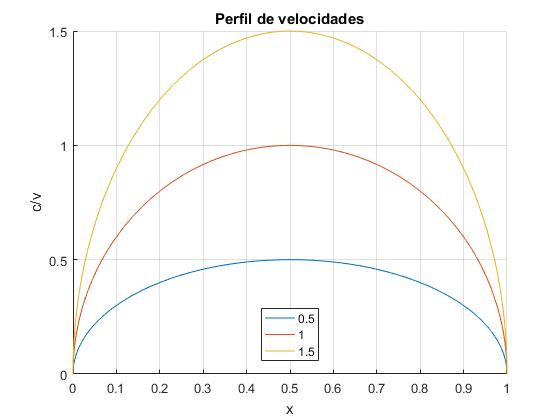
La velocidad de la corriente tiene un perfil parabólico
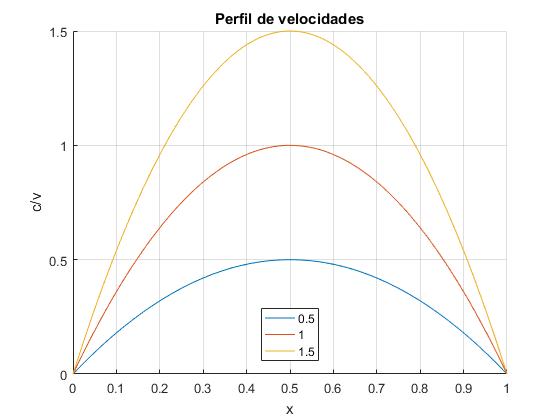
Una situación más realista se produce cuando en ambas orillas x=0 y x=d la velocidad de la corriente es nula c=0 y es máxima en el centro. Consideremos el siguiente perfil que no se menciona en el artículo citado en las referencias y sin embargo, la trayectoria se calcula de forma muy simple
d=1;
hold on
for s=0.5:0.5:1.5
y=@(x) 4*s*(x.*(d-x))/d;
fplot(y,[0,1],'displayName',num2str(s))
end
hold off
grid on
legend('-DynamicLegend','location','south')
xlabel('x')
ylabel('c/v')
title('Perfil de velocidades')
La ecuación de la trayectoria es
La constante C1 se determina a partir de las condiciones iniciales, x=0,
Tomamos la raíz positiva de la ecuación de segundo grado en C1
b=0;
d=1;
hold on
for s=[0.5,1,1.1,1.5,2]
C1=(-b/d+sqrt(b^2/d^2+1));
y=@(x) (d-x).*(C1*exp(-2*s*x.^2/d)-exp(2*s*x.^2/d)/C1)/2+b;
fplot(y,[0,1], 'displayName',num2str(s))
end
ylim([-1.5,0])
legend('-DynamicLegend','location','southwest')
hold off
grid on
xlabel('x')
ylabel('y')
title('Canoa')
Calculamos numéricamente el tiempo de viaje
b=0;
d=1;
%tiempo de viaje
for s=[0.5,1,1.1,1.5,2]
C1=(-b/d+sqrt(b^2/d^2+1));
f=@(x) (C1*exp(-2*s*x.^2/d)+exp(2*s*x.^2/d)/C1)/2;
t=integral(f,0,d);
disp([s,t])
end
0.5000 1.1047
1.0000 1.4813
1.1000 1.6054
1.5000 2.3633
2.0000 4.3337
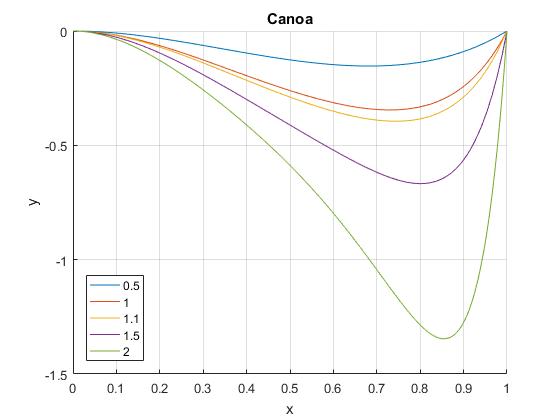
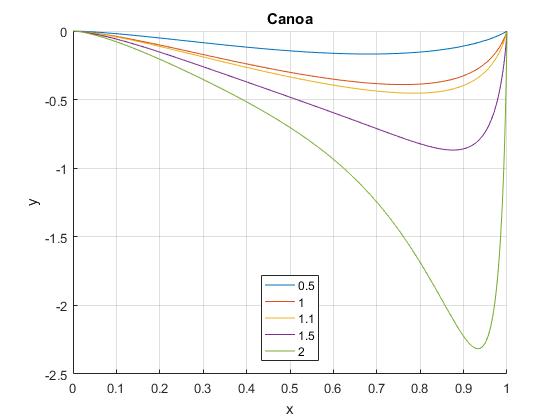
La velocidad de la corriente tiene el siguiente perfil
Otra situación realista se produce cuando en ambas orillas x=0 y x=d la velocidad de la corriente es nula c=0 y es máxima en el centro. Consideremos el perfil
d=1;
hold on
for s=0.5:0.5:1.5
y=@(x) 2*s*sqrt(x.*(d-x))/d;
fplot(y,[0,1],'displayName',num2str(s))
end
hold off
grid on
legend('-DynamicLegend','location','south')
xlabel('x')
ylabel('c/v')
title('Perfil de velocidades')
Se hace el cambio de variable
>> syms x d; >> z=int(sqrt(x/(d-x)),x); >> simplify(z) ans =d*atan((x/(d - x))^(1/2)) - (d - x)*(x/(d - x))^(1/2)
La ecuación de la trayectoria es
La constante C1 se determina a partir de las condiciones iniciales, x=0,
Tomamos la raíz positiva de la ecuación de segundo grado en z=exp(C)
b=0;
d=1;
hold on
for s=[0.5,1,1.1,1.5,2]
C=log(-b/d+sqrt(b^2/d^2+1));
y=@(x) (d-x).*sinh(2*s*(sqrt(x.*(d-x))-d*atan(sqrt(x./(d-x))))/d+C)+b;
fplot(y,[0,1],'displayName',num2str(s))
end
%ylim([-1,0])
hold off
legend('-DynamicLegend','location','south')
grid on
xlabel('x')
ylabel('y')
title('Canoa')
Referencias
M J O'Shea. Crossing a river in a canoe -how complicated can it get?. Eur. J. Phys. 31 (2010) pp. 857-862
Indian National Physics Olympiad. Homi Bhabha Centre for Science Eduaction. Solved papers NSEP & INPhO, 2016-2018, Example 12, pp. 11

