En primer lugar, volvemos a revisar el problema original, del torpedo a la caza de un submarino, o del barco pirata al asalto de un barco mercante, para que puedan compararse las dos soluciones al mismo problema

La luz se propaga con velocidad infinita

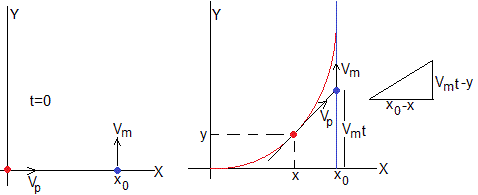
El barco mercante se mueve a lo largo de la línea recta x=x₀ con velocidad constante V_m partiendo del punto (x₀,0) en el instante t=0. Mientras, el barco pirata parte del origen con velocidad constante V_p

En el instante t, el barco mercante se encuentra en la posición (x₀, V_mt). En dicho instante, el barco pirata se encuentra en la posición (x,y), su vector velocidad ${\overrightarrow{V}}_p$ (cuya dirección es tangente a la trayectoria) apunta al barco mercante

${\displaystyle \frac{dy}{dx}=\frac{V_{m}t-y}{x_0-x}}$

El barco pirata recorre con velocidad constante V_p el camino que une el origen con el punto (x,y) en un tiempo t. La longitud del camino es

${\displaystyle \begin{array}{l}{\displaystyle \underset{A}{\overset{B}{\int }}ds=}{\displaystyle \underset{A}{\overset{B}{\int }}\sqrt{d{x}^2+d{y}^2}=}{\displaystyle \underset{A}{\overset{B}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}\\ V_{p}t={\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}dx\end{array}}$

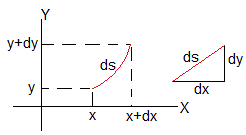
Sustituimos el tiempo t en la primera ecuación. Denominamos p=dy/dx

${\displaystyle \begin{array}{l}\frac{V_m}{V_p}{\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{1+p^2}}dx=y+\left(x_0-x\right)p\\ \alpha {\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{1+p^2}}dx=y+\left(x_0-x\right)p\end{array}}$

Derivamos respecto de x

${\displaystyle \begin{array}{l}\alpha \sqrt{1+p^2}=p+\left(x_0-x\right)\frac{dp}{dx}-p\\ \alpha \sqrt{1+p^2}=\left(x_0-x\right)\frac{dp}{dx}\end{array}}$

Integramos esta ecuación diferencial, sabiendo que para x=0, p=dy/dx=0

${\displaystyle \begin{array}{l}\alpha {\displaystyle \underset{0}{\overset{x}{\int }}\frac{dx}{x_0-x}={\displaystyle \underset{0}{\overset{p}{\int }}\frac{dp}{\sqrt{1+p^2}}}}\\ {-\alpha \ln \left(x_0-x\right)|}_0^x={\ln \left(p+\sqrt{1+p^2}\right)|}_0^p\\ \alpha \ln \frac{x_0}{x_0-x}=\ln \left(p+\sqrt{1+p^2}\right)\\ {\left(\frac{x_0}{x_0-x}\right)}^{\alpha }=p+\sqrt{1+p^2}\\ {\left(1-\frac{x}{x_0}\right)}^{-2\alpha }-2p{\left(1-\frac{x}{x_0}\right)}^{-\alpha }+p^2=1+p^2\\ {\left(1-\frac{x}{x_0}\right)}^{-2\alpha }-1=2p{\left(1-\frac{x}{x_0}\right)}^{-\alpha }\\ \frac{dy}{dx}=\frac{1}{2}\left\{{\left(1-\frac{x}{x_0}\right)}^{-\alpha }-{\left(1-\frac{x}{x_0}\right)}^{\alpha }\right\}\end{array}}$

Integramos, sabiendo que el pirata parte del origen x=0, y=0

${\displaystyle \begin{array}{l}\frac{dy}{dx}=\frac{1}{2}\left\{{\left(1-\frac{x}{x_0}\right)}^{-\alpha }-{\left(1-\frac{x}{x_0}\right)}^{\alpha }\right\}\\ {\displaystyle \underset{0}{\overset{y}{\int }}dy}=\frac{1}{2}{\displaystyle \underset{0}{\overset{x}{\int }}\left\{{\left(1-\frac{x}{x_0}\right)}^{-\alpha }-{\left(1-\frac{x}{x_0}\right)}^{\alpha }\right\}dx}\\ y={\frac{1}{2}\left\{-\frac{x_0}{-\alpha +1}{\left(1-\frac{x}{x_0}\right)}^{-\alpha +1}+\frac{x_0}{\alpha +1}{\left(1-\frac{x}{x_0}\right)}^{\alpha +1}\right\}|}_0^x\\ y=\frac{x_0}{2}\left\{\frac{1}{1+\alpha }{\left(1-\frac{x}{x_0}\right)}^{1+\alpha }-\frac{1}{1-\alpha }{\left(1-\frac{x}{x_0}\right)}^{1-\alpha }\right\}+\frac{\alpha x_0}{1-{\alpha }^2},\alpha =\frac{V_m}{V_p}<1\end{array}}$

Representamos las trayectorias de persecución para dos valores del parámetro α=0.7 y 1.5

x0=1;
hold on
for a=[1.5,0.7]
    f=@(x) x0*((1-x/x0).^(1+a)/(1+a)-(1-x/x0).^(1-a)/(1-a))/2+a*x0/(1-a^2);
    fplot(f,[0,x0])
end
line([0,x0], [f(x0),f(x0)], 'lineStyle','--')
hold off
grid on
ylim([0,5])
xlabel('x')
ylabel('y')
title('Trayectorias de persecución')

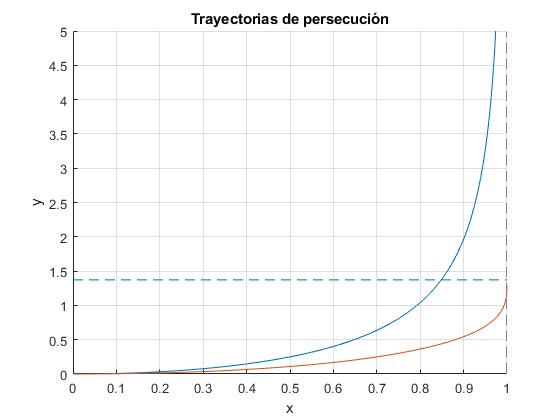
Para α≥1, no hay encuentro, y→∞ cuando x→x₀

Para α=0.7, el encuentro entre los dos barcos se produce para y=1.4 aproximadamente

>> f(x0)
ans =    1.3725

la luz se propaga con velocidad finita

Sustituimos los barcos por naves espaciales, supongamos que la velocidad de propagación de la luz c ya no es infinita sino comparable a las velocidades V_m y V_p de las dos naves espaciales. Sin embargo, analizaremos el problema en el marco de la mecánica Newtoniana

El aspecto fundamental de este problema es que en un instante t, el vector velocidad de la nave pirata ${\overrightarrow{V}}_p$ apunta en la dirección en la que ve a la nave mercante. Como a la señal luminosa emitida por la nave mercante le lleva un tiempo en alcanzar la nave pirata, su posición habrá cambiado.

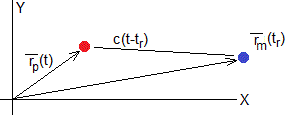
La posición de la nave pirata es ${\overrightarrow{r}}_p(t)$ en el instante t, cuando recibe la señal y la posición de la nave mercante es ${\overrightarrow{r}}_m(t_r)$ cuando la emitió en un instante anterior t_r. Si la señal se propaga con velocidad c, el tiempo entre la emisión y recepción de la señal es t-t_r

${\displaystyle c\left(t-t_r\right)=\left|{\overrightarrow{r}}_m(t_r)-{\overrightarrow{r}}_p(t)\right|}$

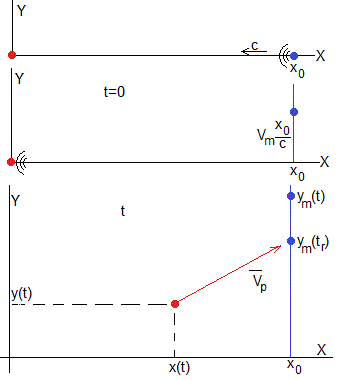
Situación inicial

El instante t=0, la señal emitida por la nave mercante alcanza la nave pirata situada en el origen. Como la primera señal viaja una distancia x₀, la posición de la nave mercante en dicho instante es (x₀, V_mx₀/c).

Situación en el instante t

En el instante t la nave mercante está situada en el punto (x₀, y_m(t)), con

${\displaystyle y_m(t)=V_m\frac{x_0}{c}+V_{m}t}$

El vector velocidad de la nave pirata ${\overrightarrow{V}}_p$ apunta en la dirección en la que ve a la nave mercante, (la posición de la nave mercante y_m(t_r) en el instante t_r en la que emitió la señal). La dirección del vector velocidad es tangente a la trayectoria de persecución

${\displaystyle \frac{dy}{dx}=\frac{y_m(t_r)-y}{x_0-x}=\frac{V_m\frac{x_0}{c}+V_m{t}_r-y}{x_0-x}}$

que junto con la definición del tiempo t_r,

${\displaystyle c\left(t-t_r\right)=\sqrt{{\left(x_0-x\right)}^2+{\left(y_m(t_r)-y\right)}^2}}$

definen la trayectoria de persecución teniendo en cuenta la velocidad finita de propagación de la luz. Para ello, tenemos que eliminar el tiempo t_r del sistema de dos ecuaciones

En la primera ecuación, despejamos y_m(t_r)-y

${\displaystyle \begin{array}{l}\frac{dy}{dx}=\frac{y_m(t_r)-y}{x_0-x}\\ y_m(t_r)-y=\left(x_0-x\right)\frac{dy}{dx}\end{array}}$

Introducimos en la segunda

${\displaystyle c\left(t-t_r\right)=\left(x_0-x\right)\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}$

Despejamos t_r en la primera ecuación y sustituimos en ésta última

${\displaystyle \begin{array}{l}{t}_r=\frac{x_0-x}{V_m}\frac{dy}{dx}+\frac{y}{V_m}-\frac{x_0}{c}\\ ct-c\frac{x_0-x}{V_m}\frac{dy}{dx}-c\frac{y}{V_m}+x_0=\frac{x_0-x}{c}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}\end{array}}$

El barco pirata recorre con velocidad constante V_p un camino que une el origen con el punto (x,y) en un tiempo t. La longitud del camino es

${\displaystyle V_{p}t={\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}dx}$

Introducimos el tiempo t en la última ecuación

${\displaystyle \begin{array}{l}\frac{c}{V_p}{\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}-c\frac{x_0-x}{V_m}\frac{dy}{dx}-c\frac{y}{V_m}+x_0=\left(x_0-x\right)\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}\\ \frac{c}{V_p}{\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{1+p^2}dx}-c\frac{x_0-x}{V_m}p-c\frac{y}{V_m}+x_0=\left(x_0-x\right)\sqrt{1+p^2},p=\frac{dy}{dx}\end{array}}$

Derivando respecto de x

${\displaystyle \begin{array}{l}\frac{c}{V_p}\sqrt{1+p^2}+\frac{c}{V_m}p-\frac{c}{V_m}\left(x_0-x\right)\frac{dp}{dx}-\frac{c}{V_m}p=-\sqrt{1+p^2}+\left(x_0-x\right)p\frac{dp}{dx}\frac{1}{\sqrt{1+p^2}}\\ \left(\frac{c}{V_p}+1\right)\sqrt{1+p^2}-\frac{c}{V_m}\left(x_0-x\right)\frac{dp}{dx}=\left(x_0-x\right)p\frac{dp}{dx}\frac{1}{\sqrt{1+p^2}}\\ \left(\frac{c}{V_p}+1\right)\left(1+p^2\right)-\frac{c}{V_m}\left(x_0-x\right)\frac{dp}{dx}\sqrt{1+p^2}=\left(x_0-x\right)p\frac{dp}{dx}\\ \left(\frac{1}{\beta }+1\right)\left(1+p^2\right)-\frac{1}{\alpha \beta }\left(x_0-x\right)\frac{dp}{dx}\sqrt{1+p^2}=\left(x_0-x\right)p\frac{dp}{dx},\{\begin{array}{l}\alpha =\frac{V_m}{V_p}\\ \beta =\frac{V_p}{c}\end{array}\\ \alpha \left(1+\beta \right)\left(1+p^2\right)=\left(x_0-x\right)\left(\alpha \beta p+\sqrt{1+p^2}\right)\frac{dp}{dx}\end{array}}$

Caso particular: cuando β→0 (la velocidad de propagación de la luz se hace infinita), recuperamos la ecuación diferencial de la trayectoria de persecución del primer apartado

${\displaystyle \begin{array}{l}\alpha \left(1+p^2\right)-\left(x_0-x\right)\frac{dp}{dx}\sqrt{1+p^2}=0\\ \alpha \sqrt{1+p^2}-\left(x_0-x\right)\frac{dp}{dx}=0\end{array}}$

Integramos la última ecuación, sabiendo que para x=0, p=dy/dx=0

${\displaystyle \begin{array}{l}\alpha \left(1+\beta \right)\frac{dx}{x_0-x}=\frac{\left(\alpha \beta p+\sqrt{1+p^2}\right)}{1+p^2}dp\\ \alpha \left(1+\beta \right){\displaystyle \underset{0}{\overset{x}{\int }}\frac{dx}{x_0-x}}=\alpha \beta {\displaystyle \underset{0}{\overset{p}{\int }}\frac{p}{1+p^2}}dp+{\displaystyle \underset{0}{\overset{p}{\int }}\frac{dp}{\sqrt{1+p^2}}}\\ \alpha \left(1+\beta \right)\ln \frac{x_0}{x_0-x}=\frac{1}{2}\alpha \beta \ln \left(1+p^2\right)+\ln \left(p+\sqrt{1+p^2}\right)\\ {\left(\frac{x_0}{x_0-x}\right)}^{\alpha \left(1+\beta \right)}={\left(1+p^2\right)}^{\alpha \beta /2}\left(p+\sqrt{1+p^2}\right)\\ {\left(1-\frac{x}{x_0}\right)}^{-\alpha \left(1+\beta \right)}={\left(1+p^2\right)}^{\alpha \beta /2}\left(p+\sqrt{1+p^2}\right)\end{array}}$

Ahora, tenemos una función implícita de x en función de p=dy/dx. No podemos despejar dy/dx e integrar de forma analítica o numérica con la condición inicial de que la nave pirata parte del origen, x=0, y=0.

Para obtener la ecuación de la trayectoria de persecución, y=f(x) procedemos del siguiente manera:

• Despejamos x=x(p)

${\displaystyle \begin{array}{l}{\left(1-\frac{x}{x_0}\right)}^{-\alpha \left(1+\beta \right)}={\left(1+p^2\right)}^{\alpha \beta /2}\left(p+\sqrt{1+p^2}\right)\\ 1-\frac{x}{x_0}=\frac{1}{{\left\{{\left(1+p^2\right)}^{\alpha \beta /2}\left(p+\sqrt{1+p^2}\right)\right\}}^{1/(\alpha \left(1+\beta \right))}}\\ \frac{x}{x_0}=1-\frac{1}{{\left\{{\left(1+p^2\right)}^{\alpha \beta /2}\left(p+\sqrt{1+p^2}\right)\right\}}^{1/\left(\alpha \left(1+\beta \right)\right)}}\end{array}}$

• Creamos una tabla de datos x, p que guardaamos en los vectores pp y xx

    x0=1;
    a=0.5; %alfa
    b=0.8; %beta
    %tabal de valors x, p
    f=@(p) 1-1./((1+p.^2).^(a*b/2).*(p+sqrt(1+p.^2)).^(1/(a*(1+b))));
    pp=0:0.1:100;
    xx=f(pp);

• Utilizamos un procedimiento de integración numérica. En este caso, se ha elegido el método Simpson 1/3

function suma=simpson(ff,x0,xf,n)
    %n número par de intervalos, n+1 número de puntos en el vector    
        x=linspace(x0,xf,n+1);   
        h=x(2)-x(1);
        suma=ff(x(1))+ff(x(n+1));
        for i=2:2:n
            suma=suma+4*ff(x(i));
        end
        for i=3:2:n-1
            suma=suma+2*ff(x(i));
        end
        suma=suma*h/3;
    end
end

• Para un valor de x que no esté en la tabla, el correspondiente valor de p se determina mediante interpolación lineal utilizando la función interp1 de MATLAB

    function  y=curva(x)
        y=interp1(xx,pp,x,'linear');
    end

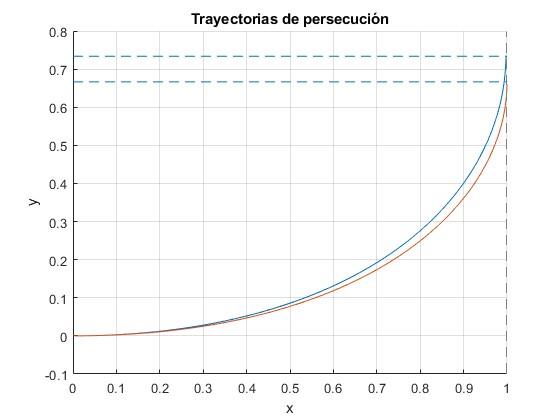
Representamos la trayectoria de persecución para α=0.5 y β=0.8, tomando x₀=1. Se compara con la trayectoria de persecución cuando la velocidad c tiende a infinito, β→0, deducida en el primer apartado

function persecucion_9
    x0=1;
    a=0.5; %alfa
    b=0.8; %beta
    %tabal de valors x, p
    f=@(p) 1-1./((1+p.^2).^(a*b/2).*(p+sqrt(1+p.^2)).^(1/(a*(1+b))));
    pp=0:0.1:100;
    xx=f(pp);
    x1=0:0.002:x0-0.002;
    y1=zeros(length(x1),1);
    k=1;
    for xk=x1
        y1(k)=simpson(@curva, 0,xk,50);
        k=k+1;
    end
    hold on
    plot(x1,y1)
    line([0,x0],[y1(end),y1(end)],'lineStyle','--')
    %instantánea
    f=@(x) x0*((1-x/x0).^(1+a)/(1+a)-(1-x/x0).^(1-a)/(1-a))/2+a*x0/(1-a^2);
    fplot(f,[0,x0])
    line([0,x0],[f(x0),f(x0)],'lineStyle','--')
    hold off
    grid on
    xlabel('x')
    ylabel('y')
    title('Trayectorias de persecución')

    function  y=curva(x)
        y=interp1(xx,pp,x,'linear');
    end

    function suma=simpson(ff,x0,xf,n)
    %n número par de intervalos, n+1 número de puntos en el vector    
        x=linspace(x0,xf,n+1);   
        h=x(2)-x(1);
        suma=ff(x(1))+ff(x(n+1));
        for i=2:2:n
            suma=suma+4*ff(x(i));
        end
        for i=3:2:n-1
            suma=suma+2*ff(x(i));
        end
        suma=suma*h/3;
    end
end

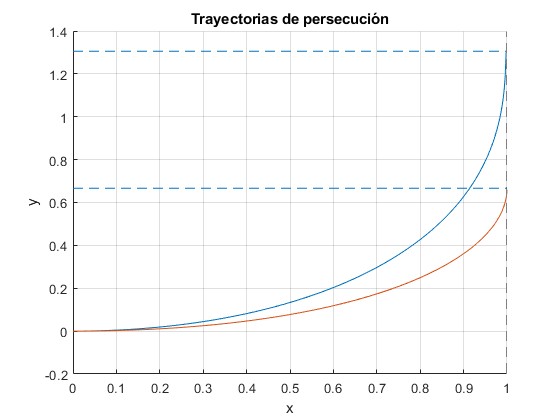
Cuando la velocidad c es muy grande y β es muy pequeño. Por ejemplo, α=0.5 y β=0.1. Ambas trayectorias casi se superponen

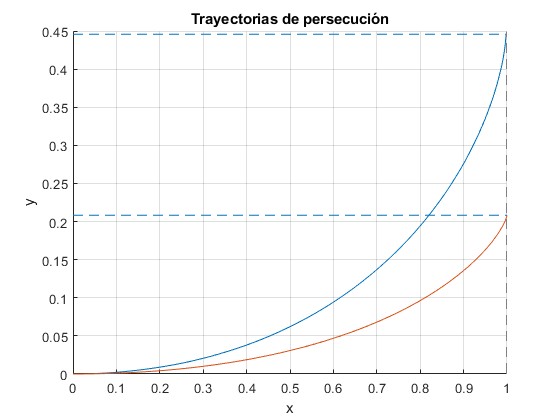
Un último ejemplo, α=0.2 y β=0.99

Referencias

Thales Azevedo, Anderson Pelluso. Space pirates: A pursuit curve problem involving retarded time. Am. J. Phys. 90 (10), October 2022. pp. 730-735