Estas curvas se generan con un juguete denominado spirograph (un juguete para dibujar jugando) en el que ruedas dentadas pueden rodar sobre circunferencias u otras curvas cerradas fijas.

Se fija la curva base al papel (habitualmente, un anillo de plástico) y se elige una rueda dentada que puede rodar por el interior del anillo o por el exterior. Se introduce la punta del bolígrafo a través de un agujero situado a distancias variables del centro de la rueda y se comienza a girar. El bolígrafo dibuja una trayectoria sobre el papel. El atractivo del juego está en la vistosidad y complejidad de las trayectorias generadas mediante movimientos simples. Se distinguen unas trayectorias de otras dibujándolas con bolígrafos de varios colores.

Epicicloide

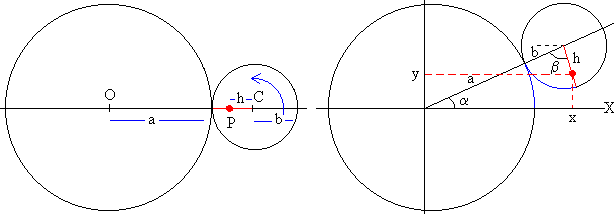
En la figura, se muestra la geometría de la epitrocoide en la cual un círculo de radio b rueda por el exterior de un círculo fijo de radio a. La distancia OC entre los centros de ambos círculos es (a+b), y sea h la distancia entre el centro del círculo móvil C y el punto P.

En la figura de la izquierda, se muestra la situación inicial y en la figura de la derecha, la situación al cabo de un cierto tiempo t, cuando la línea que une los centros de ambos círculos OC forma un ángulo α con la horizontal.

El ángulo β girado por el radio CP está en relación inversa al radio del círculo móvil. Como vemos en la figura, los arcos (en azul) tienen la misma longitud, por tanto,

a·α =b·β

Las coordenadas del punto P serán

x=(a+b)·cosα +h·sin(α +β -90)
y=(a+b)·sinα -h·cos(α +β -90)

o bien,

${\displaystyle \begin{array}{l}x=(a+b)\cos \alpha -h\cos \left(\frac{a+b}{b}\alpha \right)\\ y=(a+b)\sin \alpha -h\sin \left(\frac{a+b}{b}\alpha \right)\end{array}}$

Hipocicloide

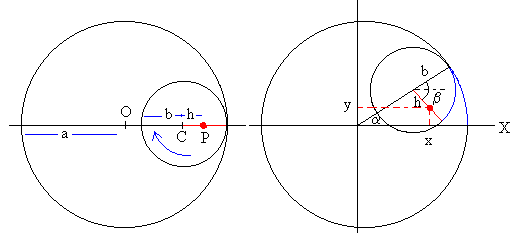
En el caso de que el círculo móvil ruede por el interior del círculo fijo, el punto C está a una distancia (a-b) de O. Al cabo de un cierto tiempo t, cuando la líneas OC que une los centros de los dos círculos forme un ángulo α con la horizontal, las coordenadas del punto P serán

x=(a-b)·cosα +h·cos(β-α)
y=(a-b)·sinα -h·sin(β-α)

o bien,

${\displaystyle \begin{array}{l}x=(a-b)\cos \alpha +h\cos \left(\frac{a-b}{b}\alpha \right)\\ y=(a-b)\sin \alpha -h\sin \left(\frac{a-b}{b}\alpha \right)\end{array}}$

En el caso del spirograph cada círculo tiene un número entero de dientes, m el anillo fijo, y n el círculo móvil. Como en número de dientes es proporcional a sus respectivos radios

m/n=a/b

Por ejemplo, si la rueda móvil tiene 48 dientes y la fija 144, la relación es 144/48= 3/1. El círculo móvil al rodar alrededor del círculo fijo completa una vuelta para volver al punto de partida, pero gira tres vueltas completas alrededor de su eje C.

Si la rueda móvil tiene 96 dientes y la fija 144, la relación es 144/96= 3/2. El círculo móvil al rodar a lo largo del círculo fijo completa dos vueltas para volver al punto de partida y gira alrededor de su eje C tres vueltas.

Las expresiones de x e y para ambos tipos de curvas

${\displaystyle \{\begin{array}{l}x=b\left(\frac{m}{n}+\delta \right)\cos \alpha -\delta h\cos \left(\left(\frac{m}{n}+\delta \right)\alpha \right)\\ y=b\left(\frac{m}{n}+\delta \right)\sin \alpha -h\sin \left(\left(\frac{m}{n}+\delta \right)\alpha \right)\end{array}\{\begin{array}{l}\delta =\mathrm{1,}\text{ epicicloide}\\ \delta =-\mathrm{1,}\text{ hipocicloide}\end{array}}$

Los casos particulares más importantes son aquellos en los que n=1 y h=b. En este caso, b=a/m, las ecuaciones parámétricas se escriben

${\displaystyle \{\begin{array}{l}x=a\left(1+\frac{\delta }{m}\right)\cos \alpha -\frac{\delta }{m}a\cos \left((m+\delta )\alpha \right)\\ y=a\left(1+\frac{\delta }{m}\right)\sin \alpha -\frac{1}{m}a\sin \left((m+\delta )\alpha \right)\end{array}\{\begin{array}{l}\delta =\mathrm{1,}\text{epiciloide}\\ \delta =-\mathrm{1,}\text{hipocicloide}\end{array}}$

Ejemplos

1. Hipocicloides

• El círculo fijo tiene 96 dientes y el móvil 24 dientes y P está en el borde del círculo.

delta=-1;
b=1; 
h=b;
m=4; n=1;
x=@(t) b*(m/n+delta)*cos(t)-delta*h*cos((m/n+delta)*t);
y=@(t) b*(m/n+delta)*sin(t)-h*sin((m/n+delta)*t);
fplot(x,y,[0,n*2*pi])
axis equal
xlabel('x')
ylabel('y')
grid on
title('Hipocicloide')



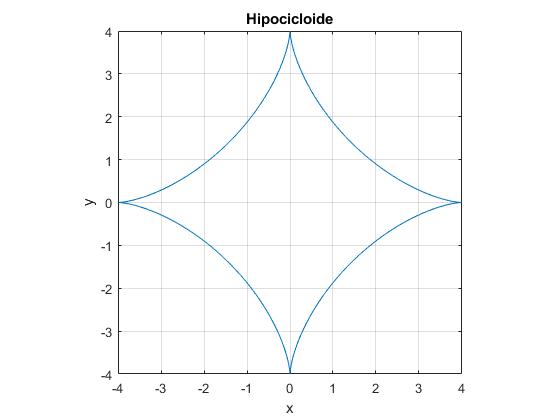
• El círculo fijo tiene 96 dientes y el móvil 48

• Si el punto P no está en el borde del círculo se obtiene una elipse
• Si P está en el borde del círculo se obtiene un segmento
• Si P está en el centro del círculo móvil C, se obtiene una circunferencia.

2. Epicicloides

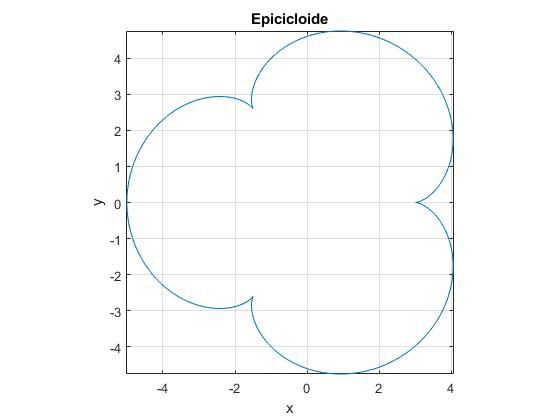
• El círculo fijo tiene 96 dientes y el móvil tiene 32 dientes, el punto P está en el borde del círculo.

delta=1;
b=1; 
h=b;
m=3; n=1;
x=@(t) b*(m/n+delta)*cos(t)-delta*h*cos((m/n+delta)*t);
y=@(t) b*(m/n+delta)*sin(t)-h*sin((m/n+delta)*t);
fplot(x,y,[0,n*2*pi])
axis equal
xlabel('x')
ylabel('y')
grid on
title('Epicicloide')



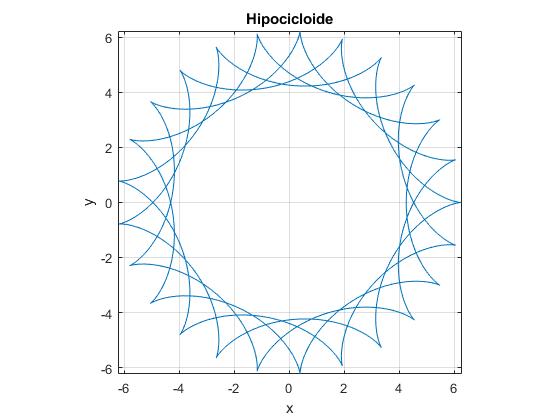
• Otros ejemplos

delta=-1;
b=1; %interior
h=b;
m=25; n=4; %rueda fija, 150 y rueda móvil, 24
x=@(t) b*(m/n+delta)*cos(t)-delta*h*cos((m/n+delta)*t);
y=@(t) b*(m/n+delta)*sin(t)-h*sin((m/n+delta)*t);
fplot(x,y,[0,n*2*pi])
axis equal
xlabel('x')
ylabel('y')
grid on
title('Hipocicloide')

Actividades

• Se elige la rueda móvil y la rueda fija, especificando el número de los dientes en los controles de selección respectivos.
• Se establece la posición del punto P, normalmente en el borde de la rueda móvil, actuando en la barra de desplazamiento.
• Se elige si el círculo móvil rodará por el interior o exterior, activando el botón de radio correspondiente.

Se pulsa el botón titulado Nuevo.

Referencias

Robert J. Whitaker. Harmonographs. II Circular design (Apendix). Am. J. Phys. 69(2) February 2001. pp.179-180