Coordenadas polares, cilíndricas y esféricas

Polares

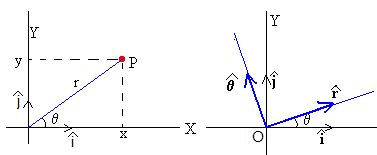
Tiene por origen O y vectores unitaros, $\hat{r}$ y $\hat{θ}$

Relación entre los vectores unitarios

$\begin{array}{l} \hat{r} = \cos θ \cdot \hat{i} + \sin θ \cdot \hat{j} \\ \hat{θ} = - \sin θ \cdot \hat{i} + \cos θ \cdot \hat{j} \end{array}$

Derivadas de los vectores unitarios

$\begin{array}{l} \frac{d \hat{r}}{d t} = (- \sin θ \cdot \hat{i} + \cos θ \cdot \hat{j}) \frac{d θ}{d t} = \frac{d θ}{d t} \hat{θ} \\ \frac{d \hat{θ}}{d t} = - (\cos θ \cdot \hat{i} + \sin θ \cdot \hat{j}) \frac{d θ}{d t} = - \hat{r} \frac{d θ}{d t} \end{array}$

Vector posición

$\vec{r} = r \hat{r}$

Vector velocidad

$\vec{v} = \frac{d \vec{r}}{d t} = \frac{d (r \hat{r})}{d t} = \frac{d r}{d t} \hat{r} + r \frac{d \hat{r}}{d t} = \frac{d r}{d t} \hat{r} + r \frac{d θ}{d t} \hat{θ}$

Vector aceleración

$\begin{array}{l} \frac{d^{2} \vec{r}}{d t^{2}} = \frac{d \vec{v}}{d t} = \frac{d^{2} r}{d t^{2}} \hat{r} + \frac{d r}{d t} \frac{d \hat{r}}{d t} + (r \frac{d^{2} θ}{d t^{2}} + \frac{d r}{d t} \frac{d θ}{d t}) \hat{θ} + r \frac{d θ}{d t} \frac{d \hat{θ}}{d t} = \\ \frac{d^{2} r}{d t^{2}} \hat{r} + \frac{d r}{d t} \frac{d θ}{d t} \hat{θ} + (r \frac{d^{2} θ}{d t^{2}} + \frac{d r}{d t} \frac{d θ}{d t}) \hat{θ} - r {(\frac{d θ}{d t})}^{2} \hat{r} = \\ (\frac{d^{2} r}{d t^{2}} - r {(\frac{d θ}{d t})}^{2}) \hat{r} + (r \frac{d^{2} θ}{d t^{2}} + 2 \frac{d r}{d t} \frac{d θ}{d t}) \hat{θ} \end{array}$

Cilíndricas

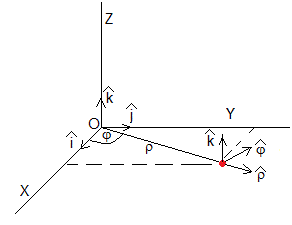
Tiene por origen O y vectores unitaros, $\hat{ρ}$ , $\hat{φ}$ y $\hat{k}$

Relación entre los vectores unitarios

$\begin{array}{l} \hat{ρ} = \cos φ \hat{i} + \sin φ \hat{j} \\ \hat{φ} = - \sin φ \hat{i} + \cos φ \hat{j} \end{array}$

Derivadas de los vectores unitarios

$\begin{array}{l} \frac{d \hat{ρ}}{d t} = (- \sin φ \hat{i} + \cos φ \hat{j}) \frac{d φ}{d t} = \frac{d φ}{d t} \hat{φ} \\ \frac{d \hat{φ}}{d t} = (- \cos φ \hat{i} - \sin φ \hat{j}) \frac{d φ}{d t} = - \frac{d φ}{d t} \hat{ρ} \end{array}$

Vector posición

$\vec{r} = ρ \hat{ρ} + z \hat{k}$

Vector velocidad

$\begin{array}{l} \vec{v} = \frac{d \vec{r}}{d t} = \frac{d ρ}{d t} \hat{ρ} + ρ \frac{d \hat{ρ}}{d t} + \frac{d z}{d t} \hat{k} \\ \vec{v} = \frac{d ρ}{d t} \hat{ρ} + ρ \frac{d φ}{d t} \hat{φ} + \frac{d z}{d t} \hat{k} \end{array}$

Vector aceleración

$\begin{array}{l} \frac{d^{2} \vec{r}}{d t^{2}} = \frac{d \vec{v}}{d t} = \frac{d^{2} ρ}{d t^{2}} \hat{ρ} + \frac{d ρ}{d t} \frac{d \hat{ρ}}{d t} + \frac{d ρ}{d t} \frac{d φ}{d t} \hat{φ} + ρ \frac{d^{2} φ}{d t^{2}} \hat{φ} + ρ \frac{d φ}{d t} \frac{d \hat{φ}}{d t} + \frac{d^{2} z}{d t^{2}} \hat{k} = \\ \frac{d^{2} ρ}{d t^{2}} \hat{ρ} + \frac{d ρ}{d t} \frac{d φ}{d t} \hat{φ} + \frac{d ρ}{d t} \frac{d φ}{d t} \hat{φ} + ρ \frac{d^{2} φ}{d t^{2}} \hat{φ} - ρ {(\frac{d φ}{d t})}^{2} \hat{ρ} + \frac{d^{2} z}{d t^{2}} \hat{k} \\ \frac{d^{2} \vec{r}}{d t^{2}} = (\frac{d^{2} ρ}{d t^{2}} - ρ {(\frac{d φ}{d t})}^{2}) \hat{ρ} + (ρ \frac{d^{2} φ}{d t^{2}} + 2 \frac{d ρ}{d t} \frac{d φ}{d t}) \hat{φ} + \frac{d^{2} z}{d t^{2}} \hat{k} \end{array}$

Esféricas

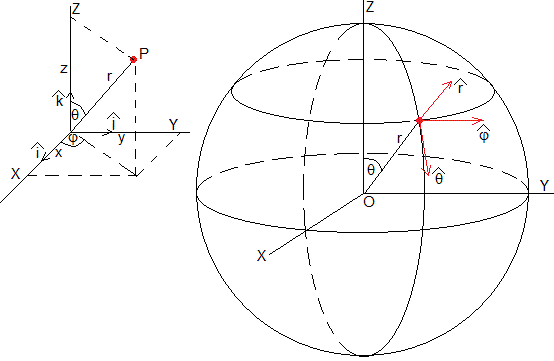
Tiene por origen O y vectores unitaros, $\hat{r}$ , $\hat{φ}$ y $\hat{θ}$

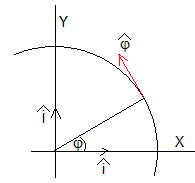
Relación entre los vectores unitarios

El vector unitario $\hat{r}$ tiene la misma dirección que el vector $\vec{r}$ pero su módulo es la unidad

$\hat{r} = \sin θ \cdot \cos φ \hat{i} + \sin θ \cdot \sin φ \hat{j} + \cos θ \hat{k}$

Como apreciamos en la figura

$\hat{φ} = - \sin φ \hat{i} + \cos φ \hat{j}$

Utilizamos el producto vectorial para obtener la expresión de $\hat{θ}$

$\hat{θ} = \hat{φ} \times \hat{r} = | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ - \sin φ & \cos φ & 0 \\ \sin θ \cdot \cos φ & \sin θ \cdot \sin φ & \cos θ \end{matrix} | = \cos θ \cdot \cos φ \hat{i} + \cos θ \sin φ \hat{j} - \sin θ \hat{k}$

Derivadas de los vectores unitarios

$\begin{array}{l} \frac{d \hat{r}}{d t} = (\cos θ \cdot \cos φ \frac{d θ}{d t} - \sin θ \sin φ \frac{d φ}{d t}) \hat{i} + (\cos θ \cdot \sin φ \frac{d θ}{d t} + \sin θ \cos φ \frac{d φ}{d t}) \hat{j} - \sin θ \frac{d θ}{d t} \hat{k} = \\ (\cos θ \cdot \cos φ \hat{i} + \cos θ \cdot \sin φ \hat{j} - \sin θ \hat{k}) \frac{d θ}{d t} + (- \sin φ \hat{i} + \cos φ \hat{j}) \sin θ \cdot \frac{d φ}{d t} = \\ \frac{d θ}{d t} \hat{θ} + \sin θ \cdot \frac{d φ}{d t} \hat{φ} \end{array}$

$\begin{array}{l} \frac{d \hat{θ}}{d t} = (- \sin θ \cdot \cos φ \frac{d θ}{d t} - \cos θ \cdot \sin φ \frac{d φ}{d t}) \hat{i} + (- \sin θ \cdot \sin φ \frac{d θ}{d t} + \cos θ \cdot \cos φ \frac{d φ}{d t}) \hat{j} - \cos θ \frac{d θ}{d t} \hat{k} = \\ - (\sin θ \cos φ \hat{i} + \sin θ \cdot \sin φ \hat{j} + \cos θ \hat{k}) \frac{d θ}{d t} + (- \sin φ \hat{i} + \cos φ \hat{j}) \cos θ \frac{d φ}{d t} = \\ - \frac{d θ}{d t} \hat{r} + \cos θ \frac{d φ}{d t} \hat{φ} \end{array}$

Utilizamos el producto vectorial para obtener la derivada de este vector unitario

$\begin{array}{l} \hat{φ} = \hat{r} \times \hat{θ} \\ \frac{d \hat{φ}}{d t} = \frac{d \hat{r}}{d t} \times \hat{θ} + \hat{r} \times \frac{d \hat{θ}}{d t} = (\frac{d θ}{d t} \hat{θ} + \sin θ \cdot \frac{d φ}{d t} \hat{φ}) \times \hat{θ} + \hat{r} \times (- \frac{d θ}{d t} \hat{r} + \cos θ \frac{d φ}{d t} \hat{φ}) = \\ \sin θ \cdot \frac{d φ}{d t} \hat{φ} \times \hat{θ} + \cos θ \frac{d φ}{d t} \hat{r} \times \hat{φ} = = (- \sin θ \cdot \hat{r} - \cos θ \cdot \hat{θ}) \frac{d φ}{d t} \end{array}$

Vector posición

$\vec{r} = r \hat{r}$

Vector velocidad

$\frac{d \vec{r}}{d t} = \frac{d r}{d t} \hat{r} + r \frac{d \hat{r}}{d t} = \frac{d r}{d t} \hat{r} + r \frac{d θ}{d t} \hat{θ} + r \sin θ \cdot \frac{d φ}{d t} \hat{φ}$

Vector aceleración

$\begin{array}{l} \frac{d^{2} \vec{r}}{d t^{2}} = \frac{d}{d t} (\frac{d \vec{r}}{d t}) = \frac{d^{2} r}{d t^{2}} \hat{r} + \frac{d r}{d t} \frac{d \hat{r}}{d t} + \frac{d r}{d t} \frac{d θ}{d t} \hat{θ} + r \frac{d^{2} θ}{d t^{2}} \hat{θ} + r \frac{d θ}{d t} \frac{d \hat{θ}}{d t} + \frac{d r}{d t} \sin θ \frac{d φ}{d t} \hat{φ} + r \cos θ \frac{d θ}{d t} \frac{d φ}{d t} \hat{φ} + r \sin θ \frac{d^{2} φ}{d t^{2}} \hat{φ} + r \sin θ \frac{d φ}{d t} \frac{d \hat{φ}}{d t} = \\ \frac{d^{2} r}{d t^{2}} \hat{r} + \frac{d r}{d t} (\frac{d θ}{d t} \hat{θ} + \sin θ \cdot \frac{d φ}{d t} \hat{φ}) + \frac{d r}{d t} \frac{d θ}{d t} \hat{θ} + r \frac{d^{2} θ}{d t^{2}} \hat{θ} + r \frac{d θ}{d t} (- \frac{d θ}{d t} \hat{r} + \cos θ \frac{d φ}{d t} \hat{φ}) + \frac{d r}{d t} \sin θ \frac{d φ}{d t} \hat{φ} + r \cos θ \frac{d θ}{d t} \frac{d φ}{d t} \hat{φ} + r \sin θ \frac{d φ}{d t} (- \sin θ \cdot \hat{r} - \cos θ \cdot \hat{θ}) \frac{d φ}{d t} \end{array}$

El resultado es

$\begin{array}{l} \frac{d^{2} \vec{r}}{d t^{2}} = (\frac{d^{2} r}{d t^{2}} - r {(\frac{d θ}{d t})}^{2} - r \sin^{2} θ {(\frac{d φ}{d t})}^{2}) \hat{r} + \\ (r \frac{d^{2} θ}{d t^{2}} + 2 \frac{d r}{d t} \frac{d θ}{d t} - r \sin θ \cdot \cos θ {(\frac{d φ}{d t})}^{2}) \hat{θ} + \\ (r \sin θ \frac{d^{2} φ}{d t^{2}} + 2 \sin θ \frac{d r}{d t} \frac{d φ}{d t} + 2 r \cos θ \frac{d θ}{d t} \frac{d φ}{d t}) \hat{φ} \end{array}$