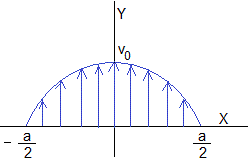
Un nadador intenta cruzar un río moviéndose con velocidad constante c sobre el agua. El río tiene una anchura a, la velocidad de la corriente en su centro es máxima v₀ y nula en las orillas. Supondremos que el perfil de la velocidad es

${\displaystyle v(x)=v_0\left(1-4\frac{x^2}{a^2}\right)}$

que se corresponde con perfil de velocidades de un líquido viscoso que circula en régimen laminar en un tubo de radio a/2 en función de la distancia radial x a su eje

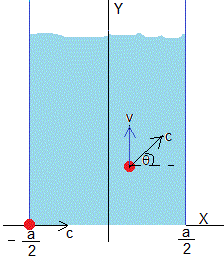
El nadador parte de la posición (-a/2,0) y se mueve sobre el agua hacia la derecha con velocidad constante c, haciendo un ángulo θ=0, con la horizontal

Cuando se encuentra en la posición (x,y), la velocidad del nadador (respecto de tierra) será la suma vectorial de la velocidad del nadador sobre el agua, $\overrightarrow{c}=c·\cos \theta \widehat{i}+c·\sin \theta \widehat{j}$ y la velocidad de la corriente en dicha posición $\overrightarrow{v}=v(x)\widehat{j}$

${\displaystyle \overrightarrow{c}+\overrightarrow{v}=c·\cos \theta \widehat{i}+\left(c·\sin \theta +v(x)\right)\widehat{j}}$

Vamos a determinar la trayectoria que deberá seguir el nadador para emplear un tiempo mínimo T en cruzar el río.

${\displaystyle T={\displaystyle \underset{-a/2}{\overset{a/2}{\int }}\frac{dx}{c·\cos \theta }}}$

c·cosθ es la velocidad horizontal (a lo largo del eje X) del nadador. Dado que la velocidad del nadador $\overrightarrow{c}+\overrightarrow{v}$, es tangente a la trayectoria. Calculamos la pendiente dy/dx

${\displaystyle \dot{y}=\frac{dy}{dx}=\frac{c·\sin \theta +v(x)}{c·\cos \theta }=\frac{\sin \theta +\vartheta (x)}{\cos \theta },\vartheta (x)=\frac{v_0}{c}\left(1-4\frac{x^2}{a^2}\right)}$

Despejamos cosθ. Tenemos en cuenta que para que el nadador alcance la orilla derecha, -π/2≤θ≤π/2, cosθ tiene que ser positivo

${\displaystyle \begin{array}{l}\sin \theta =\dot{y}\cos \theta -\vartheta (x)\\ \left({\dot{y}}^2+1\right){\cos }^2\theta -2\dot{y}·\vartheta (x)\cos \theta +{\vartheta }^2(x)-1=0\\ \cos \theta =\frac{\dot{y}·\vartheta (x)+\sqrt{{\dot{y}}^2+1-{\vartheta }^2(x)}}{{\dot{y}}^2+1}\end{array}}$

El tiempo que tarda el nadador en cruzar el río es

${\displaystyle T\left[y(x)\right]=\frac{1}{c}{\displaystyle \underset{-a/2}{\overset{a/2}{\int }}\frac{{\dot{y}}^2+1}{\dot{y}·\vartheta (x)+\sqrt{{\dot{y}}^2+1-{\vartheta }^2(x)}}}dx}$

Ecuación de la trayectoria

Se tratará de encontrar la ecuación de la trayectoria y=y(x) que hace que el tiempo que tarda el nadador T en cruzar el río sea mínimo.

Aplicamos la ecuación de Euler-Lagrange,

${\displaystyle \frac{\partial f}{\partial y}-\frac{d}{dx}\left(\frac{\partial f}{\partial \dot{y}}\right)=0}$

a un funcional que no depende de la variable y

${\displaystyle f(x,y,\dot{y})=\frac{{\dot{y}}^2+1}{\dot{y}·\vartheta (x)+\sqrt{{\dot{y}}^2+1-{\vartheta }^2(x)}}}$

Por este motivo, la obtención de la ecuación de la trayectoria es más sencilla. Derivamos el funcional f respecto a $\dot{y}$

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial \dot{y}}=C_1\\ \frac{1}{1-{\vartheta }^2(x)}\left\{\frac{\dot{y}}{\sqrt{{\dot{y}}^2+1-{\vartheta }^2(x)}}-\vartheta (x)\right\}=C_1\end{array}}$

La constante C₁ de determina sabiendo que en la posición inicial x=-a/2, y=0, dy/dx=tanθ=0. Dado que ϑ(-a/2)=0, se concluye que C₁=0

Despejamos dy/dx e integramos para obtener la ecuación de la trayectoria y=y(x)

${\displaystyle \begin{array}{l}\dot{y}=\vartheta (x)\sqrt{{\dot{y}}^2+1-{\vartheta }^2(x)}\\ \dot{y}=\vartheta (x)\\ \frac{dy}{dx}=\frac{v_0}{c}\left(1-4\frac{x^2}{a^2}\right)\\ y=\frac{v_0}{c}\left(x-\frac{4}{3}\frac{x^3}{a^2}\right)+C_2\end{array}}$

Determinamos la constante C₂ sabiendo que para x=-a/2, y=0. La ecuación de la trayectoria es

${\displaystyle y=\frac{v_0}{c}\left(x-\frac{4}{3}\frac{x^3}{a^2}+\frac{a}{3}\right)}$

Cuando el nadador llega a la orilla opuesta x=a/2, su desviación es

${\displaystyle y=\frac{v_0}{c}\left(\frac{2}{3}a\right)}$

Dibujamos las trayectorias que describe un nadador que parte de la orilla izquierda de un río de anchura a=2, para tres valores del cociente v₀/c: 0.5, 1 y 1.5.

a=2; %anchura del río
hold on
for k=[0.5,1,1.5] %cociente v0/c
    fplot(@(x) k*(x-4*x.^3/(3*a^2)+a/3),[-a/2,a/2], 'displayName',num2str(k))
end
hold off
grid on  
legend('-DynamicLegend','location','northwest')
xlabel('x')
ylabel('y')
title('nadador que atraviesa un río')

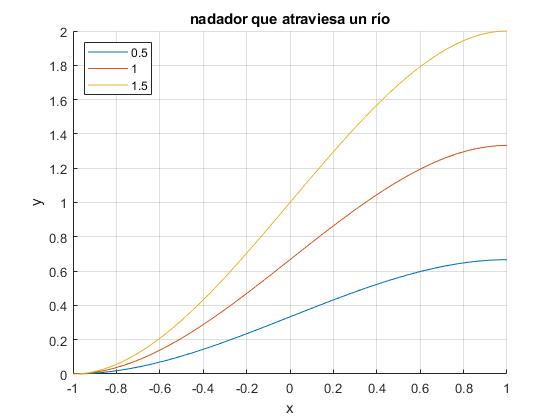
La trayectoria es simétrica respecto de la recta horizontal que pasa por el punto $\left(\mathrm{0,}\frac{v_0}{c}\frac{a}{3}\right)$, este es el punto de inflexión de la trayectoria.

Velocidad de la corriente constante

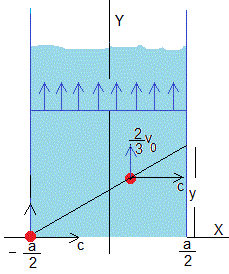
La velocidad de la corriente en el río es máxima en el centro y nula en las orillas. La velocidad media de la corriente de agua en el río es

${\displaystyle <v>={\displaystyle \underset{-a/2}{\overset{a/2}{\int }}{v}_0\left(1-4\frac{x^2}{a^2}\right)dx=\frac{2}{3}{v}_0}}$

Supongamos un río cuya corriente lleve una velocidad uniforme e igual a la velocidad media 2v₀/3. La velocidad c del nadador en el agua es constante y se dirige hacia la orilla opuesta partiendo de x=-a/2.

El nadador sigue la trayectoria rectilínea de la figura, empleando un tiempo t=a/c, en alcanzar la orilla opuesta y desviándose

${\displaystyle y=\frac{2}{3}{v}_0\left(\frac{a}{c}\right)=\frac{v_0}{c}\left(\frac{2}{3}a\right)}$

El mismo resultado que hemos obtenido previamente, suponiendo que la corriente tiene un perfil de velocidades parabólico, la velocidad es máxima en el centro y nula en las orillas

Referencias

Vladimir Ivchenko. Using Poiseuille flow: a refined solution of the riverboat problem. Eur. J. Phys. 40 (2019) 015002