En el efecto fotoeléctrico solamente hemos considerado que el fotón tiene una energía E=hf . Ahora bien, un fotón también tiene un momento lineal p=E/c=hf/c.

Esta relación no es nueva, sino que surge al plantear las ecuaciones que describen las ondas electromagnéticas. La radiación electromagnética tiene momento y energía. Cuando analicemos cualquier proceso en el que la radiación electromagnética interactúa con las partículas cargadas debemos de aplicar las leyes de conservación de la energía y del momento lineal.

En el caso del efecto fotoeléctrico, no se aplicó la ley de conservación del momento lineal por que el electrón estaba ligado a un átomo, a una molécula o a un sólido, la energía y el momento absorbidos están compartidos por el electrón y el átomo, la molécula o el sólido con los que está ligado.

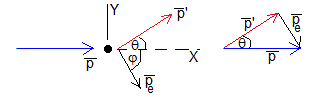
Vamos a obtener la fórmula del efecto Compton a partir del estudio de un choque elástico entre un fotón y un electrón inicialmente en reposo.

1. Principio de conservación del momento lineal

• Sea $\overrightarrow{p}$ el momento lineal del fotón incidente,

${\displaystyle p=\frac{E}{c}=\frac{hf}{c}=\frac{h}{\lambda }}$

• Sea $\overrightarrow{p}\text{'}$ el momento lineal del fotón difundido,

${\displaystyle p\text{'}=\frac{E\text{'}}{c}=\frac{hf\text{'}}{c}=\frac{h}{\lambda \text{'}}}$

• Sea $\overrightarrow{p_e}$ es el momento lineal del electrón después del choque, se verificará que

${\displaystyle \overrightarrow{p}=\overrightarrow{p_e}+\overrightarrow{p\text{'}}\{\begin{array}{l}p=p\text{'}\cos \theta +p_e\cos \phi \\ 0=p\text{'}\sin \theta -p_e\sin \phi \end{array}}$

La relación de módulos es

${\displaystyle p_e^2={\left(\frac{h}{\lambda }\right)}^2+{\left(\frac{h}{\lambda \text{'}}\right)}^2-2\frac{h^2}{\lambda \lambda \text{'}}\cos \theta }$

2. Principio de conservación de la energía

• La energía del fotón incidente es E=hf=hc/λ

• La energía del fotón dispersado es E’=hf’=hc/λ'.

• La energía del electrón en antes del choque que está en reposo es m_ec². Después del choque es

${\displaystyle c\sqrt{m_e^2{c}^2+p_e^2}}$

donde m_e es la masa en reposo del electrón 9.1·10^-31 kg

El principio de conservación de la energía se escribe

${\displaystyle \frac{hc}{\lambda }+m_e{c}^2=\frac{hc}{\lambda \text{'}}+c\sqrt{m_e^2{c}^2+p_e^2}}$

Resolvemos el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}{\left(\frac{hc}{\lambda }-\frac{hc}{\lambda \text{'}}+m_e{c}^2\right)}^2=m_e^2{c}^4+p_e^2{c}^2\\ {\left(\frac{hc}{\lambda }\right)}^2+{\left(\frac{hc}{\lambda \text{'}}\right)}^2+m_e^2{c}^4-2\frac{h^2{c}^2}{\lambda \lambda \text{'}}+2\frac{h}{\lambda }{m}_e{c}^3-2\frac{h}{\lambda \text{'}}{m}_e{c}^3=m_e^2{c}^4+\left({\left(\frac{h}{\lambda }\right)}^2+{\left(\frac{h}{\lambda \text{'}}\right)}^2-2\frac{h^2}{\lambda \lambda \text{'}}\cos \theta \right)c^2\\ -\frac{h}{\lambda \lambda \text{'}}+\frac{1}{\lambda }{m}_{e}c-\frac{1}{\lambda \text{'}}{m}_{e}c=-\frac{h}{\lambda \lambda \text{'}}\cos \theta \end{array}}$

Multiplicando por λλ', el resultado es

${\displaystyle \lambda \text{'}-\lambda =\frac{h}{m_{e}c}\left(1-\cos \theta \right)}$

Hemos obtenido el valor de la constante de proporcionalidad λ_c a partir de las constantes fundamentales h, m_e y c.

Calculamos la dirección φ del electrón después del choque. De la conservación del momento lineal

${\displaystyle \{\begin{array}{l}{p}_e\sin \phi =\frac{h}{\lambda \text{'}}\sin \theta \\ p_e\cos \phi =\frac{h}{\lambda }-\frac{h}{\lambda \text{'}}\cos \theta \end{array}}$

Eliminamos el momento lineal del electrón p_e

${\displaystyle \begin{array}{l}\tan \phi =\frac{\frac{1}{\lambda \text{'}}\sin \theta }{\frac{1}{\lambda }-\frac{1}{\lambda \text{'}}\cos \theta }=\frac{\lambda \sin \theta }{\lambda \text{'}-\lambda \cos \theta }=\frac{\lambda \sin \theta }{\lambda \text{'}-\lambda \cos \theta }=\frac{\lambda \sin \theta }{\lambda +\frac{h}{m_{e}c}\left(1-\cos \theta \right)-\lambda \cos \theta }\\ \tan \phi =\frac{\sin \theta }{\left(1+\frac{h}{m_{e}c}\right)\left(1-\cos \theta \right)}=\frac{1}{\left(1+\frac{h}{m_{e}c}\right)\tan \left(\frac{\theta }{2}\right)}\end{array}}$

Llegamos entonces a la conclusión de que podemos explicar la dispersión de la radiación electromagnética por los electrones libres como una colisión elástica entre un fotón y un electrón en reposo en el sistema de referencia del observador. A partir de las ecuaciones de conservación del momento lineal y de la energía, llegamos a la ecuación que nos relaciona la longitud de onda de la radiación incidente λ con la longitud de onda de la radiación dispersada λ’ y con el ángulo de dispersión θ .

Actividades

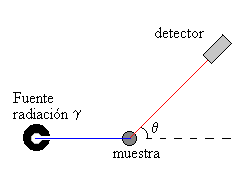
En la experiencia real, el detector es un cristal de INa, la fuente de rayos gamma está producida por el isótopo Cs-137, que tiene un pico muy agudo centrado en 661.6 keV, o en la longitud de onda 1.878 10^-12 m, (0.01878 A). Los electrones libres los proporciona un trozo de metal que puede ser una varilla de hierro.

Midiendo la diferencia de longitudes de onda entre la radiación dispersada y la radiación incidente se pide calcular la constante λ_C. A partir del valor de esta constante, y conocida los valores de las constantes fundamentales, velocidad de la luz c=3·10⁸ m/s y la masa del electrón m_e=9.1·10^-31 kg, se pide calcular el valor de la constante h de Planck, comprobando que está cerca del valor 6.63·10^-34 Js.

• Se cambia el ángulo θ del detector en el control titulado Angulo

Se pulsa el botón titulado Nuevo

Se mide la longitud de onda de la radiación dispersada.

Ejemplo:

La longitud de onda de la radiación dispersada para el ángulo 60º es λ^'=0.03091 A. Calcular la constante λ_C y a continuación, la constante h de Planck.

0.03091-0.01878=λ_C(1-cos60)
λ_C=0.02426 A=2.426·10^-12 m

${\displaystyle 2.426·{10}^{-12}=\frac{h}{9.1·{10}^{-31}·3·{10}^8}h=6.623·{10}^{-34}\text{Js}}$

En la parte inferior izquierda, se representa la intensidad de la radiación gamma que registra el detector en función de la longitud de onda. En el programa interactivo, la fuente de rayos gamma emite ondas electromagnéticas cuyas longitudes de onda están centradas en 0.01878 A. La forma del pico se ha representado mediante la gaussiana

${\displaystyle y=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left(x-a\right)}^2}{2{\sigma }^2}\right)}$

centrada en dicha longitud de onda a, y cuyo valor sigma σ se ha ajustado para dar la apariencia de un pico agudo (en color azul). La radiación registrada por el detector se ha representado por medio de otra gaussiana (en color rojo) centrada en la longitud de onda dispersada cuyo valor de sigma σ va creciendo con el ángulo de dispersión.

En la parte inferior derecha, se muestran los valores numéricos de las longitudes de onda en angstrong (10^-10 m) de la radiación incidente y dispersada.

En la parte derecha, vemos de forma animada el choque elástico entre un fotón y un electrón en reposo. Observamos cómo cambia la longitud de onda de la radiación dispersada a medida que aumenta el ángulo de dispersión.

El electrón retrocede adquiriendo un momento lineal p_e y formando un ángulo que se puede calcular a partir de las ecuaciones de conservación del momento lineal (1) y de la energía (2). Para calcular la velocidad v del electrón, necesitamos la expresión relativista del momento lineal

${\displaystyle p_e=\frac{m_{e}v}{\sqrt{1-\frac{v^2}{c^2}}}}$

Efecto Compton inverso

En el efecto Compton inverso, el fotón gana energía a expensas del electrón incidente, este hecho tiene importancia en Astrofísica como mecanismo para la producción de radiación X y gamma en el espacio.

Choque frontal

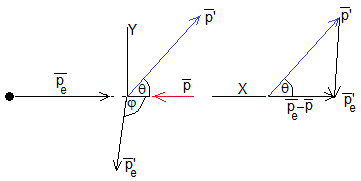
Supongamos un electrón de energía E_e y un fotón cuya energía hf se mueven en la misma dirección pero en sentido opuesto, por lo que chocan.

• Conservación del momento lineal

${\displaystyle \begin{array}{l}\overrightarrow{p_e}+\overrightarrow{p}=\overrightarrow{p\text{'}}+\overrightarrow{p{\text{'}}_e}\\ \{\begin{array}{l}{p}_e-p=p\text{'}\cos \theta +p{\text{'}}_e\cos \phi \\ 0=p\text{'}\sin \theta -p{\text{'}}_e\sin \phi \end{array}\end{array}}$

El módulo del momento final del electrón p'_e es

${\displaystyle \begin{array}{l}p{\text{'}}_e^2=p{\text{'}}^2+{\left(p_e-p\right)}^2-2p\text{'}\left(p_e-p\right)\cos \theta \\ p{\text{'}}_e^2{c}^2={\left(hf\text{'}\right)}^2+{\left(p_{e}c-hf\right)}^2-2hf\text{'}\left(p_{e}c-hf\right)\cos \theta \end{array}}$

• Conservación de la energía

${\displaystyle E_e+hf=c\sqrt{m_e^2{c}^2+p{\text{'}}_e^2}+hf\text{'}}$

Eliminamos el momento final del electrón p'_e y despejamos la frecuencia final del fotón f'

${\displaystyle \begin{array}{l}{\left(E_e+hf-hf\text{'}\right)}^2=p{\text{'}}_e^2{c}^2+m_e^2{c}^4\\ p_e^2{c}^2+m_e^2{c}^4+{\left(hf\right)}^2+{\left(hf\text{'}\right)}^2+2E_{e}hf-2E_{e}hf\text{'}-2h^{2}ff\text{'}={\left(hf\text{'}\right)}^2+{\left(p_{e}c-hf\right)}^2-2hf\text{'}\left(p_{e}c-hf\right)\cos \theta +m_e^2{c}^4\end{array}}$

El resulado es

${\displaystyle f\text{'}=\frac{p_{e}c+E_e}{hf+E_e-\left(p_{e}c-hf\right)\cos \theta }f}$

Otra forma de expresar la energía del electrón

${\displaystyle E_e=c\sqrt{m_e^2{c}^2+p_e^2}=\frac{m_e{c}^2}{\sqrt{1-\frac{v^2}{c^2}}}=\gamma m_e{c}^2}$

La frecuencia final del fotón f' es

${\displaystyle f\text{'}=\frac{\sqrt{{\gamma }^2-1}+\gamma }{\frac{hf}{m_e{c}^2}+\gamma -\left(\sqrt{{\gamma }^2-1}-\frac{hf}{m_e{c}^2}\right)\cos \theta }f}$

La frecuencia final del fotón f' es máxima cuando θ=0

${\displaystyle f{\text{'}}_m=\frac{\gamma +\sqrt{{\gamma }^2-1}}{2\frac{hf}{m_e{c}^2}+\gamma -\sqrt{{\gamma }^2-1}}f}$

Si el electrón incidente lleva una velocidad próxima a la luz, γ>>1

${\displaystyle \sqrt{{\gamma }^2-1}=\gamma \sqrt{1-\frac{1}{{\gamma }^2}}\approx \gamma \left(1-\frac{\frac{1}{{\gamma }^2}}{2}+\mathrm{...}\right)=\gamma -\frac{1}{2\gamma }}$

>> syms x;
>> taylor(sqrt(1-x^2),x)
 ans =- x^4/8 - x^2/2 + 1

La frecuencia final del fotón f' se aproxima a

${\displaystyle f{\text{'}}_m\approx \frac{\gamma +\left(\gamma -\frac{1}{2\gamma }\right)}{2\frac{hf}{m_e{c}^2}+\gamma -\left(\gamma -\frac{1}{2\gamma }\right)}f=\frac{2\gamma -\frac{1}{2\gamma }}{2\frac{hf}{m_e{c}^2}+\frac{1}{2\gamma }}f}$

Sea γ=200 y λ=500 nm, longitud de onda del fotón incidente

Los datos de las constantes: velocidad de la luz, c=2.9979·10⁸ m/s, constante de Planck h=6.6256·10^-34 Js, masa del electrón m_e=9.1091·10^-31 kg. Energía 1 eV=1.6021·10^-19 J

La energía del fotón incidente es

${\displaystyle hf=h\frac{c}{\lambda }=2.4796\text{eV}}$

La energía en reposo del electrón m_ec²=0.5110 MeV, por lo que la energía del fotón incidente hf<<m_ec²

La energía del fotón después del choque es hf'=3.9520·10⁵ eV=0.3952 MeV. La longitud de onda correspondiente es, λ=c/f'=3.1372·10^-12 m=3.1372·10^-3 nm

c=2.9979e8; %velocidad de la luz
h=6.6256e-34; %constante h de Planck
me=9.1091e-31; %masa en reposo del electrón
eV=1.6021e-19; %un electron-voltio

g=200; %gamma
lambda=500e-9; %longitud de onda
f=c/lambda; %frecuencia
fp=(2*g-1/(2*g))*f/(2*h*f/(me*c^2)+1/(2*g));
disp(h*fp/eV) %energía final del fotón
disp(c/fp) %longitud de onda final

   3.9520e+05
   3.1372e-12

De la conservación del momento lineal obtenemos el ángulo de desviación φ del electrón

${\displaystyle \{\begin{array}{l}p{\text{'}}_e\cos \phi =p_e-p-p\text{'}\cos \theta \\ p{\text{'}}_e\sin \phi =p\text{'}\sin \theta \end{array}}$

Dividiendo ambas expresiones

${\displaystyle \tan \phi =\frac{\frac{hf\text{'}}{c}\sin \theta }{p_e-\frac{hf}{c}-\frac{hf\text{'}}{c}\cos \theta }=\frac{hf\text{'}\sin \theta }{\sqrt{E_e^2-m_e^2{c}^4}-hf-hf\text{'}\cos \theta }}$

Choque a 90°

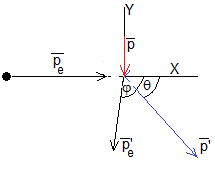
• Conservación del momento lineal

${\displaystyle \begin{array}{l}\overrightarrow{p_e}+\overrightarrow{p}=\overrightarrow{p\text{'}}+\overrightarrow{p{\text{'}}_e}\\ \{\begin{array}{l}{p}_e=p\text{'}\cos \theta +p{\text{'}}_e\cos \phi \\ p=p\text{'}\sin \theta +p{\text{'}}_e\sin \phi \end{array}\end{array}}$

El módulo del momento final del electrón p'_e es

${\displaystyle \begin{array}{l}\{\begin{array}{l}cp{\text{'}}_e\cos \phi =c{p}_e-hf\text{'}\cos \theta \\ cp{\text{'}}_e\sin \phi =hf-hf\text{'}\sin \theta \end{array}\\ c^{2}p{\text{'}}_e^2=c^2{p}_e^2+{\left(hf\text{'}\right)}^2+{\left(hf\right)}^2-2c{p}_{e}hf\text{'}\cos \theta -2h^{2}ff\text{'}\sin \theta \end{array}}$

• Conservación de la energía

${\displaystyle E_e+hf=c\sqrt{m_e^2{c}^2+p{\text{'}}_e^2}+hf\text{'}}$

Eliminamos el momento final del electrón p'_e y despejamos la frecuencia final del fotón f'

${\displaystyle \begin{array}{l}{\left(E_e+hf-hf\text{'}\right)}^2=p{\text{'}}_e^2{c}^2+m_e^2{c}^4\\ p_e^2{c}^2+m_e^2{c}^4+{\left(hf\right)}^2+{\left(hf\text{'}\right)}^2+2E_{e}hf-2E_{e}hf\text{'}-2h^{2}ff\text{'}=c^2{p}_e^2+{\left(hf\text{'}\right)}^2+{\left(hf\right)}^2-2c{p}_{e}hf\text{'}\cos \theta -2h^{2}ff\text{'}\sin \theta +m_e^2{c}^4\end{array}}$

El resultado es

${\displaystyle f\text{'}=\frac{E_e}{hf+E_e-p_{e}c\cos \theta -hf\sin \theta }f}$

La frecuencia final del fotón f' alcanza un máximo cuando

${\displaystyle \begin{array}{l}\frac{df}{d\theta }=0\\ -p_{e}c\sin \theta -hf\cos \theta =0\\ \tan \theta =\frac{hf}{p_{e}c}\end{array}}$

Teniendo en cuenta las relaciones trigonométricas

${\displaystyle \begin{array}{l}\cos \theta =\frac{1}{\sqrt{1+{\tan }^2\theta }},\sin \theta =\frac{\tan \theta }{\sqrt{1+{\tan }^2\theta }}\\ \cos \theta =\frac{p_{e}c}{\sqrt{p_e^2{c}^2+{\left(hf\right)}^2}},\sin \theta =\frac{hf}{\sqrt{p_e^2{c}^2+{\left(hf\right)}^2}}\end{array}}$

La frecuencia máxima es

${\displaystyle f{\text{'}}_m=\frac{E_e}{hf+E_e-\sqrt{p_e^2{c}^2+{\left(hf\right)}^2}}f}$

Sea γ=200 y λ=500 nm, longitud de onda del fotón incidente

La energía del fotón después del choque es hf'=3.9520·10⁵ eV=0.19798 MeV, menor que en el caso de choque frontal

c=2.9979e8; %velocidad de la luz
h=6.6256e-34; %constante h de Planck
me=9.1091e-31; %masa en reposo del electrón
eV=1.6021e-19; %un electron-voltio

g=200; %gamma
lambda=500e-9; %longitud de onda
f=c/lambda; %frecuencia
Ee=g*me*c^2;
pe2=Ee^2-me^2*c^4;
fp=Ee*f/(h*f+Ee-sqrt(pe2+(h*f)^2));
disp(h*fp/eV)

1.9798e+05

De la conservación del momento lineal obtenemos el ángulo de desviación φ del electrón

${\displaystyle \tan \phi =\frac{hf-hf\text{'}\sin \theta }{c{p}_e-hf\text{'}\cos \theta }}$

Referencias

La descripción de la experiencia real se encuentra en University Laboratory Experiments. Physics. Volume 3. PHYWE. Pág. 5.2.12.

Asian Physics. (1st – 8th). Olympiad. Problems and Solutions. Editor Zheng Yongling. World Scientific (2010), pp. 265-270