Región rectangular

La ecuación de Schrödinger para una partícula de masa m que se mueve en un potencial V(x, y) es

${\displaystyle -\frac{{\hslash }^2}{2m}\left(\frac{{\partial }^2\psi (x,y)}{\partial x^2}+\frac{{\partial }^2\psi (x,y)}{\partial y^2}\right)+V(x,y)\psi (x,y)=E\psi (x,y)}$

Sea el potencial

${\displaystyle V(x,y)=\{\begin{array}{l}\mathrm{0,}0\le x\le ay0\le y\le b\\ \infty ,x<0\text{y}x>a\\ \infty ,y<0\text{y}x>b\end{array}}$

La función de onda es nula en el exterior del recinto rectangular. En su interior, la ecuación de Schrödinger es

${\displaystyle -\frac{{\hslash }^2}{2m}\left(\frac{{\partial }^2\psi (x,y)}{\partial x^2}+\frac{{\partial }^2\psi (x,y)}{\partial y^2}\right)=E\psi (x,y)}$

Probamos la solución Ψ(x,y)=X(x)·Y(y), variables separadas

${\displaystyle \frac{1}{X}\frac{d^{2}X}{d{x}^2}+\frac{1}{Y}\frac{d^{2}Y}{d{y}^2}=-\frac{2mE}{{\hslash }^2}}$

El primer término, es una función solamente de x, el segundo, de y. El segundo miembro, es una constante.

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{d^{2}X}{d{x}^2}=-k_x^{2}X(x)\\ \frac{d^{2}Y}{d{y}^2}=-k_y^{2}Y(y)\end{array}\\ k_x^2+k_y^2=\frac{2mE}{{\hslash }^2}\end{array}}$

Hemos convertido ecuación de Schrödinger en un sistema de dos ecuaciones diferenciales en variables separadas x, y

La solución de estas dos ecuaciones diferenciales es conocida

${\displaystyle \{\begin{array}{l}X(x)=A_x\sin \left(k_{x}x\right)+B_x\cos \left(k_{x}x\right)\\ Y(y)=A_y\sin \left(k_{y}y\right)+B_y\cos \left(k_{y}y\right)\end{array}}$

Condiciones de contorno

La solución de la ecuación de Schrödinger, Ψ(x,y) se anula en los límites de la región rectangular

• Ψ(0, y)=0, X(0)=0, B_x=0
• Ψ(x, 0)=0, Y(0)=0, B_y=0

${\displaystyle \{\begin{array}{l}X(x)=A_x\sin \left(k_{x}x\right)\\ Y(y)=A_y\sin \left(k_{y}y\right)\end{array}}$

Por otra parte,

• Ψ(a, y)=0, X(a)=0, sin(k_xa)=0, k_x=n_xπ/a, n_x=1, 2, 3, ...
• Ψ(x, b)=0, Y(b)=0, sin(k_yb)=0, k_y=n_yπ/b, n_y=1, 2, 3, ...

La solución de la ecuación de Schrödinger es

${\displaystyle \psi (x,y)=C\sin \left(\frac{n_x\pi }{a}x\right)\sin \left(\frac{n_y\pi }{b}y\right)}$

Los niveles de energía son

${\displaystyle \begin{array}{l}{k}_x^2+k_y^2=\frac{2mE}{{\hslash }^2}\\ E=\frac{{\hslash }^2{\pi }^2}{2m}\left\{{\left(\frac{n_x}{a}\right)}^2+{\left(\frac{n_y}{b}\right)}^2\right\},n_x,n_y=\mathrm{1,}\mathrm{2,}\mathrm{3....}\end{array}}$

La función de onda se normaliza de modo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}{\displaystyle \underset{0}{\overset{b}{\int }}{\left|\psi (x,y)\right|}^2}}dx·dy=1\\ C^2{\displaystyle \underset{0}{\overset{a}{\int }}{\sin }^2\left(\frac{n_x\pi }{a}x\right)dx{\displaystyle \underset{0}{\overset{b}{\int }}{\sin }^2\left(\frac{n_y\pi }{b}y\right)}}dy=1\end{array}}$

Teniendo en cuenta el resultado de la integral

${\displaystyle {\displaystyle \int {\sin }^2\left(kx\right)dx}={\displaystyle \int \frac{1-\cos \left(2kx\right)}{2}dx}=\frac{1}{2}\left(x-\frac{\sin \left(2kx\right)}{2k}\right)}$

El coeficiente C vale

${\displaystyle C^2\frac{a}{2}·\frac{b}{2}=\mathrm{1,}C=\frac{2}{\sqrt{ab}}}$

La función de onda es

${\displaystyle {\psi }_{n_x,n_y}(x,y)=\frac{2}{\sqrt{ab}}\sin \left(\frac{n_x\pi }{a}x\right)\sin \left(\frac{n_y\pi }{b}y\right)}$

En el caso de que a y b sean iguales

${\displaystyle E_{n_{x,}{n}_y}=\frac{{\hslash }^2{\pi }^2}{2m{a}^2}\left(n_x^2+n_y^2\right)}$

En la figura, se representan los niveles de energía en unidades h²π²/(ma²)

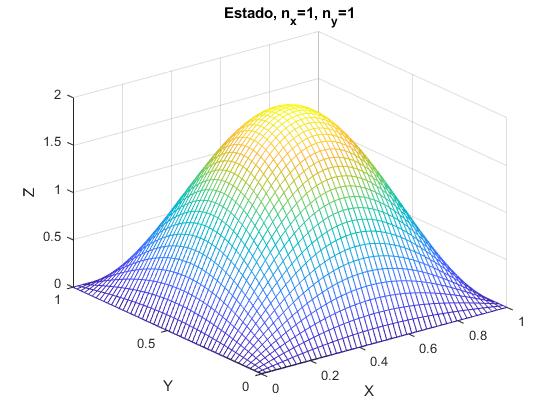
• El estado fundamental, energía más baja se obtiene para, n_x=1, n_y=1

${\displaystyle E_{\mathrm{1,1}}=\frac{{\hslash }^2{\pi }^2}{m{a}^2}}$

Representamos la función de onda correspondiente al estado fundamental

nx=1;
ny=1;
a=1;
x=linspace(0,a,50);
y=linspace(0,a,50);
[X,Y]=meshgrid(x,y);
Z=(2/a)*sin(nx*pi*X/a).*sin(ny*pi*Y/a);
mesh(X,Y,Z);
xlabel('X')
ylabel('Y')
zlabel('Z')
title('Estado, n_x=1, n_y=1')



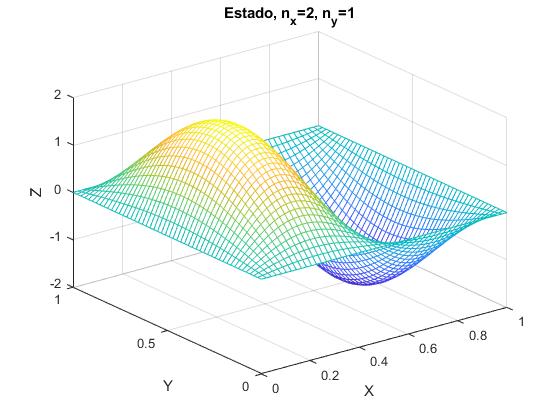
• Para el primer estado excitado, n_x=2, n_y=1 o bien, n_x=1 y n_y=2, obtenemos la misma energía

${\displaystyle E_{\mathrm{2,1}}=\frac{5}{2}\frac{{\hslash }^2{\pi }^2}{m{a}^2}}$

Cuando tenemos dos o más estados de la misma energía se denominan degenerados

nx=2;
ny=1;
a=1;
x=linspace(0,a,50);
y=linspace(0,a,50);
[X,Y]=meshgrid(x,y);
Z=(2/a)*sin(nx*pi*X/a).*sin(ny*pi*Y/a);
mesh(X,Y,Z);
xlabel('X')
ylabel('Y')
zlabel('Z')
title('Estado, n_x=2, n_y=1')

Probabilidad

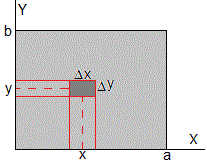
Calculamos la probabilidad de encontrar la partícula en el rectángulo sombreado de la figura cuyo centro es (x, y) y anchura Δx altura Δy.

${\displaystyle P(x,y)={\displaystyle \underset{x-\frac{\Delta x}{2}}{\overset{x+\frac{\Delta x}{2}}{\int }}{\displaystyle \underset{y-\frac{\Delta y}{2}}{\overset{y+\frac{\Delta y}{2}}{\int }}{\left|{\psi }_{n_x,n_y}(x,y)\right|}^2}}dx·dy}$

El resultado es

${\displaystyle \begin{array}{l}P(x,y)=\frac{4}{ab}{\displaystyle \underset{x-\frac{\Delta x}{2}}{\overset{x+\frac{\Delta x}{2}}{\int }}{\sin }^2\left(\frac{n_x\pi }{a}x\right)dx{\displaystyle \underset{y-\frac{\Delta y}{2}}{\overset{y+\frac{\Delta y}{2}}{\int }}{\sin }^2\left(\frac{n_y\pi }{b}y\right)}}dy=\\ \frac{1}{ab}\left(\Delta x-\frac{\sin \left(2\frac{n_x\pi }{a}x\right)\cos \left(\frac{n_x\pi }{a}\Delta x\right)}{\frac{n_x\pi }{a}}\right)\left(\Delta y-\frac{\sin \left(2\frac{n_y\pi }{b}y\right)\cos \left(\frac{n_y\pi }{b}\Delta y\right)}{\frac{n_y\pi }{b}}\right)\end{array}}$

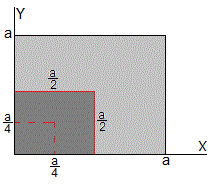
Ejemplo, sea a=b, calculamos la probabilidad de encontrar la partícula en la región sombreada (0<x<a/2), (0<y<a/2) en el estado correspondiente a n_x=1, n_y=2;

Poniendo Δx=a/2, Δy=a/2, x=a/4, y=a/4, obtenemos

${\displaystyle P\left(\frac{a}{4},\frac{a}{4}\right)=\frac{1}{a^2}\left(\frac{a}{2}-\frac{\sin \left(2\frac{\pi }{a}\frac{a}{4}\right)\cos \left(\frac{\pi }{a}\frac{a}{2}\right)}{\frac{\pi }{a}}\right)\left(\frac{a}{2}-\frac{\sin \left(2\frac{2\pi }{a}\frac{a}{4}\right)\cos \left(\frac{2\pi }{a}\frac{a}{2}\right)}{\frac{2\pi }{a}}\right)=\frac{1}{4}}$

Caja de potencial

Vamos a resolver la ecuación de Schrödinger para una partícula de masa m que se mueve en una región cuyo potencial V(x, y, z) es

${\displaystyle \{\begin{array}{l}\mathrm{0,}0\le x\le a,0\le y\le b,0\le z\le c\\ \infty ,x<0\text{y}x>a\\ \infty ,y<0\text{y}x>b\\ \infty ,z<0\text{y}z>c\end{array}}$

La ecuación de Schrödinger es

${\displaystyle -\frac{{\hslash }^2}{2m}\left(\frac{{\partial }^2\psi (x,y,z)}{\partial x^2}+\frac{{\partial }^2\psi (x,y,z)}{\partial y^2}+\frac{{\partial }^2\psi (x,y,z)}{\partial z^2}\right)+V(x,y,z)\psi (x,y,z)=E\psi (x,y,z)}$

La función de onda es nula en el exterior del recinto, en su interior la ecuación de Schrödinger es

${\displaystyle -\frac{{\hslash }^2}{2m}\left(\frac{{\partial }^2\psi (x,y,z)}{\partial x^2}+\frac{{\partial }^2\psi (x,y,z)}{\partial y^2}+\frac{{\partial }^2\psi (x,y,z)}{\partial z^2}\right)=E\psi (x,y,z)}$

Probamos la solución Ψ(x,y)=X(x)·Y(y)·Z(z), variables separadas.

${\displaystyle \frac{1}{X}\frac{d^{2}X}{d{x}^2}+\frac{1}{Y}\frac{d^{2}Y}{d{y}^2}+\frac{1}{Z}\frac{d^{2}Z}{d{z}^2}=-\frac{2mE}{{\hslash }^2}}$

El primer término, es una función solamente de x, el segundo, de y y el tercero, de z. El segundo miembro, es una constante. Esta ecuación diferencial se convierte en un sistema de tres ecuaciones diferenciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{d^{2}X}{d{x}^2}=-k_x^{2}X(x)\\ \frac{d^{2}Y}{d{y}^2}=-k_y^{2}Y(y)\\ \frac{d^{2}Z}{d{z}^2}=-k_z^{2}Y(y)\end{array}\\ k_x^2+k_y^2+k_z^2=\frac{2mE}{{\hslash }^2}\end{array}}$

Hemos convertido ecuación de Schrödinger en un sistema de tres ecuaciones diferenciales en variables separadas x, y y z

La solución de estas tres ecuaciones diferenciales es conocida

${\displaystyle \{\begin{array}{l}X(x)=A_x\sin (k_{x}x)+B_x\cos (k_{x}x)\\ Y(y)=A_y\sin (k_{y}y)+B_y\cos (k_{y}y)\\ Z(z)=A_z\sin (k_{z}z)+B_z\cos (k_{z}z)\end{array}}$

Condiciones de contorno

La solución de la ecuación de Schrödinger, Ψ(x,y,z) se anula en los límites de la región

• Ψ(0, y, z)=0, X(0)=0, B_x=0
• Ψ(x, 0, z)=0, Y(0)=0, B_y=0
• Ψ(x, y, 0)=0, Z(0)=0, B_z=0

${\displaystyle \{\begin{array}{l}X(x)=A_x\sin (k_{x}x)\\ Y(y)=A_y\sin (k_{y}y)\\ Z(z)=A_z\sin (k_{z}z)\end{array}}$

Por otra parte,

• Ψ(a, y, z)=0, X(a)=0, sin(k_xa)=0, k_x=n_xπ/a, n_x=1, 2, 3, ...
• Ψ(x, b, z)=0, Y(b)=0, sin(k_yb)=0, k_y=n_yπ/b, n_y=1, 2, 3, ...
• Ψ(x, y, c)=0, Z(c)=0, sin(k_zc)=0, k_z=n_zπ/c, n_z=1, 2, 3, ...

La solución de la ecuación de Schrödinger es

${\displaystyle \psi (x,y,z)=C\sin \left(\frac{n_x\pi }{a}x\right)\sin \left(\frac{n_y\pi }{b}y\right)\sin \left(\frac{n_z\pi }{c}z\right)}$

Los niveles de energía son

${\displaystyle \begin{array}{l}{k}_x^2+k_y^2+k_z^2=\frac{2mE}{{\hslash }^2}\\ E=\frac{{\hslash }^2{\pi }^2}{2m}\left\{{\left(\frac{n_x}{a}\right)}^2+{\left(\frac{n_y}{b}\right)}^2+{\left(\frac{n_z}{c}\right)}^2\right\}\end{array}}$

El coeficiente C se calcula, de modo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}{\displaystyle \underset{0}{\overset{b}{\int }}{\displaystyle \underset{0}{\overset{c}{\int }}{\left|\psi (x,y,z)\right|}^2}}}dx·dy·dz=1\\ C^2{\displaystyle \underset{0}{\overset{a}{\int }}{\sin }^2\left(\frac{n_x\pi }{a}x\right)dx·{\displaystyle \underset{0}{\overset{b}{\int }}{\sin }^2\left(\frac{n_y\pi }{b}y\right)}}dy·{\displaystyle \underset{0}{\overset{b}{\int }}{\sin }^2\left(\frac{n_z\pi }{c}y\right)}dz=1\\ C^2\frac{a}{2}\frac{b}{2}\frac{c}{2}=1\end{array}}$

La función de onda es

${\displaystyle {\psi }_{n_x,n_y,n_z}(x,y,z)=\sqrt{\frac{2^3}{abc}}\sin \left(\frac{n_x\pi }{a}x\right)\sin \left(\frac{n_y\pi }{b}y\right)\sin \left(\frac{n_z\pi }{c}z\right)}$

for nx=1:4
    for ny=1:4
        for nz=1:4
            E=(nx^2+ny^2+nz^2)/2;
            line([0,1],[E,E],'color','r')
        end
    end
end
ylim([0,20])

En el caso de que a y b y c sean iguales. El recinto es un cubo de lado a

${\displaystyle E_{n_{x,}{n}_y,n_z}=\frac{{\hslash }^2{\pi }^2}{2m{a}^2}\left(n_x^2+n_y^2+n_z^2\right)}$

En la figura, se representan los niveles de energía en unidades h²π²/(ma²)

El estado fundamental, energía más baja se obtiene con, n_x=1, n_x=1, n_z=1

${\displaystyle E_{\mathrm{1,1,1}}=\frac{3}{2}\frac{{\hslash }^2{\pi }^2}{m{a}^2}}$

Para el primer estado excitado, las combinaciones n_x=2, n_y=1 y n_z=1 o bien, n_x=1, n_y=2, n_z=1, o n_x=1, n_y=1, n_z=2, dan la misma energía. Tres estados degenerados

${\displaystyle E_{\mathrm{2,1,1}}=E_{\mathrm{1,2,1}}=E_{\mathrm{1,1,2}}=3\frac{{\hslash }^2{\pi }^2}{m{a}^2}}$

Sea n_x=3, n_y=2, n_z=1, (3,2,1), otras combinaciones que dan la misma energía son (3,1,2),(2,3,1), (2,1,3), (1,3,2), (1,2,3), en total 6 estados degenerados

Referencias

Particle in a 2-Dimensional Box