Modelo atómico de Bohr

Un átomo tiene una dimensión del orden de 10^-9 m. Está compuesto por un núcleo relativamente pesado (cuyas dimensiones son del orden de 10^-14 m) alrededor del cual se mueven los electrones, cada uno de carga -e (1.6 10^-19 C) y masa m_e (9.1·10^-31 kg).

El núcleo está compuesto por protones y neutrones. El número Z de protones coincide con el número de electrones en un átomo neutro. La masa de un protón o de un neutrón es aproximadamente 1850 veces la de un electrón. En consecuencia, la masa de un átomo es prácticamente igual a la del núcleo.

Sin embargo, los electrones de un átomo son los responsables de la mayoría de las propiedades atómicas que se reflejan en las propiedades macroscópicas de la materia.

El movimiento de los electrones alrededor del núcleo se explica, considerando solamente las interacciones entre el núcleo y los electrones (la interacción gravitatoria es completamente despreciable).

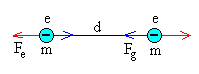
Consideremos dos electrones separados una distancia d, y comparemos la fuerza de repulsión eléctrica con fuerza de atracción entre sus masas.

${\displaystyle F_e=\frac{1}{4\pi {\epsilon }_0}\frac{e^2}{d^2}{F}_g=G\frac{m^2}{d^2}\frac{F_e}{F_g}=\frac{\text{9}\cdot {\text{10}}^{\text{9}}{\left(1.6\cdot {10}^{-19}\right)}^2}{6.67\cdot {10}^{-11}{(9.1\cdot {10}^{-31})}^2}=\text{4}\text{.17}\cdot {\text{ 10}}^{\text{42}}}$

La intensidad de la interacción gravitatoria es despreciable frente a la interacción electromagnética.

El modelo de Bohr es muy simple y recuerda al modelo planetario de Copérnico, los planetas describiendo órbitas circulares alrededor del Sol. El electrón de un átomo o ión hidrogenoide describe también órbitas circulares, pero los radios de estas órbitas no pueden tener cualquier valor.

Consideremos un átomo o ión con un solo electrón. Supondremos que el núcleo de carga Ze es un centro fijo de fuerzas.

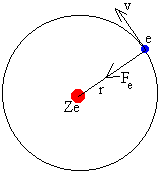
Si el electrón describe una órbita circular de radio r, por la dinámica del movimiento circular uniforme

${\displaystyle m_e\frac{v^2}{r}=\frac{Z{e}^2}{4\pi {\epsilon }_0{r}^2}}$

En el modelo de Bohr, solamente están permitidas aquellas órbitas cuyo momento angular está cuantizado.

${\displaystyle L=m_{e}vr=\frac{nh}{2\pi }n=\mathrm{1,2...}}$

n es un número entero que se denomina número cuántico, y h= 6.6256·10^-34 Js es la constante de Planck

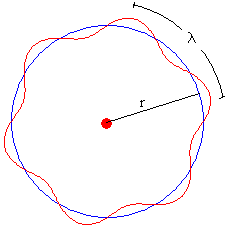
Esta regla admite otra interpretación

Para que la órbita corresponda a un estado estacionario, la longitud de la circunferencia de radio r deberá ser un múltiplo entero de la longitud de onda λ tal como se ve en la figura.

2πr=nλ

La longitud de onda de de Broglie de una partícula de masa m_e que se mueve con velocidad v es onda λ=h/p. Donde h es la constante de Planck y p=m_ev es el momento lineal del electrón.

${\displaystyle 2\pi r=n\frac{h}{m_{e}v}}$

Los radios de las órbitas permitidas son

${\displaystyle r=\frac{n^2{h}^2{\epsilon }_0}{\pi m_{e}Z{e}^2}=\frac{n^2}{Z}\frac{h^2{\epsilon }_0}{\pi m_e{e}^2}=\frac{n^2}{Z}{a}_0{a}_0=5.2917·{10}^{-11}m}$

donde a₀ se denomina radio de Bohr. a₀ es el radio de la órbita del electrón del átomo de Hidrógeno Z=1 en su estado fundamental n=1.

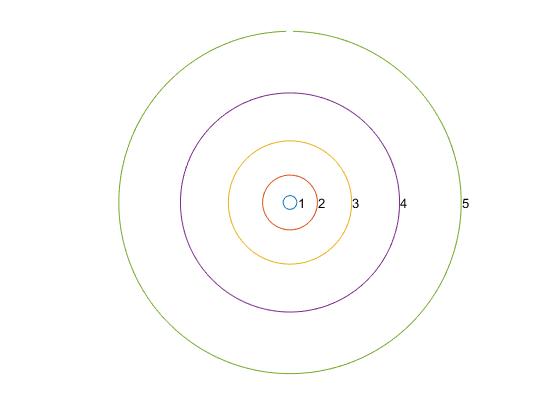
Dibujamos las posibles órbitas circulares del electrón del átomo de hidrógeno, en unidades del radio de Bohr a₀

hold on
for n=1:5
     fplot(@(t) n^2*cos(t),@(t) n^2*sin(t),[0,2*pi])
     text(n^2+0.1, 0,num2str(n))
end
hold off
axis equal
axis off

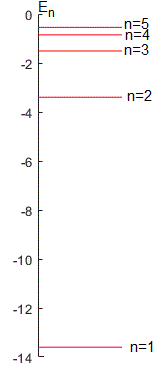
La energía total es

${\displaystyle E=\frac{1}{2}{m}_e{v}^2-\frac{1}{4\pi {\epsilon }_0}\frac{Z{e}^2}{r}=-\frac{1}{4\pi {\epsilon }_0}\frac{Z{e}^2}{2r}}$

En una órbita circular, la energía total E es la mitad de la energía potencial

${\displaystyle E=-\frac{m_e{e}^4{Z}^2}{8{\epsilon }_0^2{h}^2{n}^2}}$

La energía del electrón aumenta con el número cuántico n.

La primera energía de excitación es la que lleva a un átomo de su estado fundamental a su primer (o más bajo) estado excitado. La energía del estado fundamental se obtiene con n=1, E₁= -13.6 eV y la del primer estado excitado con n=2, E₂=-3.4 eV. Las energías se suelen expresar en electrón-voltios (1eV=1.6 10^-19 J)

La frecuencia f de la radiación emitida cuando el electrón pasa del estado excitado E₂ al fundamental E₁ es

${\displaystyle f=\frac{E_2-E_1}{h}=2.47\cdot {10}^{15}\text{Hz}}$

Modelo atómico de Sommerfeld

Vamos a derivar la ecuación de las órbitas elípticas permitidas a partir de la formulación Lagrangiana, en vez de integrar la ecuación de la energía, teniendo en cuenta la constancia del momento angular, propiedades de la fuerza de atracción (central y conservativa)

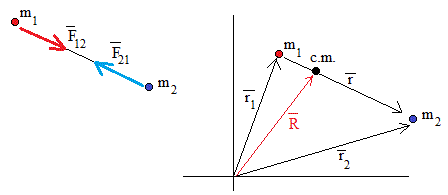
Sean dos partículas de masas m₁ y m₂ cuyas posiciones respecto de un sistema de Referencia inercial centrado en O son $\overrightarrow{r_1}$ y $\overrightarrow{r_2}$, respectivamente .

La Lagrangiana L del sistema aislado de dos partículas es

${\displaystyle L=\frac{1}{2}{m}_1{\left|\frac{d\overrightarrow{r_1}}{dt}\right|}^2+\frac{1}{2}{m}_2{\left|\frac{d\overrightarrow{r_2}}{dt}\right|}^2-E_p(r)}$

Siendo $r=\left|\overrightarrow{r_2}-\overrightarrow{r_1}\right|$, la distancia entre las dos partículas

Los dos primeros términos son las energías cinéticas de las dos partículas y el tercer término es la energía potencial de interacción entre las dos partículas

La energía potencial E_p(r) es función únicamente de esta distancia r. Para un átomo o ión hidrogenoide con un núcleo de Z protones y un electrón es

${\displaystyle E_p(r)=-\frac{1}{4\pi {\epsilon }_0}\frac{Z{q}^2}{r}=-\frac{\kappa }{r}}$

Situamos el origen del Sistema de Referencia en el centro de masas

${\displaystyle \begin{array}{l}\frac{m_1\overrightarrow{r_1}+m_2\overrightarrow{r_2}}{m_1+m_2}=0\\ \{\begin{array}{l}{m}_1\overrightarrow{r_1}+m_2\overrightarrow{r_2}=0\\ \overrightarrow{r}=\overrightarrow{r_2}-\overrightarrow{r_1}\end{array}\\ \overrightarrow{r_2}=\frac{m_1}{m_1+m_2}\overrightarrow{r},\overrightarrow{r_1}=-\frac{m_2}{m_1+m_2}\overrightarrow{r}\end{array}}$

La Lagrangiana se convierte en

${\displaystyle L=\frac{1}{2}\frac{m_1{m}_2}{m_1+m_2}{\left|\frac{d\overrightarrow{r}}{dt}\right|}^2-E_p(r)=\frac{1}{2}\mu {\left|\frac{d\overrightarrow{r}}{dt}\right|}^2-E_p(r)}$

El primer término es la energía cinética de una partícula de masa reducida μ.

En coordenadas polares se expresa

${\displaystyle L=\frac{1}{2}\mu \left({\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right)-E_p(r)}$

Ecuación del movimiento

Las ecuaciones del movimiento son

• En la dirección radial

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{r}}\right)-\frac{\partial L}{\partial r}=0\\ \mu \frac{d^{2}r}{d{t}^2}-2r{\left(\frac{d\theta }{dt}\right)}^2+\frac{d{E}_p}{dr}=0\end{array}}$

• Angular

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \mu \frac{d}{dt}\left(r^2\frac{d\theta }{dt}\right)=0\\ \mu r^2\frac{d\theta }{dt}=l\end{array}}$

Se conserva una cantidad que denominamos l, momento angular

En un sistema aislado de dos partículas interactuantes, la energía permanece constante

${\displaystyle \begin{array}{l}E=\frac{1}{2}\mu \left({\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right)+E_p(r)\\ E=\frac{1}{2}\mu \left({\left(\frac{dr}{dt}\right)}^2+\frac{l^2}{{\mu }^2{r}^2}\right)+E_p(r)=\frac{1}{2}\mu {\left(\frac{dr}{dt}\right)}^2+\frac{l^2}{2\mu r^2}+E_p(r)\end{array}}$

Ecuación de la trayectoria

Despejamos la componente radial de la velocidad dr/dt y después, obtenemos la ecuación de la trayectoria

${\displaystyle \begin{array}{l}\frac{dr}{dt}=\sqrt{\frac{2}{\mu }\left(E-E_p(r)\right)-\frac{l^2}{{\mu }^2{r}^2}}\\ \frac{dr}{dt}=\frac{dr}{d\theta }\frac{d\theta }{dt}=\frac{dr}{d\theta }\frac{l}{\mu r^2}\\ \frac{d\theta }{dr}=\frac{\frac{l}{\mu r^2}}{\sqrt{\frac{2}{\mu }\left(E-E_p(r)\right)-\frac{l^2}{{\mu }^2{r}^2}}}\\ \theta ={\displaystyle \int \frac{l}{r^2\sqrt{2\mu \left(E-E_p(r)\right)-\frac{l^2}{r^2}}}dr}\end{array}}$

En el caso de un átomo o ión hidrogenoide con un solo electrón la energía potencial es E_p(r)=-κ/r

${\displaystyle \theta (r)={\displaystyle \int \frac{l}{r^2\sqrt{2\mu \left(E+\frac{\kappa }{r}-\frac{l^2}{2\mu r^2}\right)}}dr}}$

Para integrar, llamamos u=1/r, du=-dr/r²

${\displaystyle \theta =-\frac{l}{\sqrt{2\mu }}{\displaystyle \int \frac{du}{\sqrt{E+\kappa u-\frac{l^2}{2\mu }{u}^2}}}=-{\displaystyle \int \frac{du}{\sqrt{\frac{2\mu }{l^2}E+\frac{2\mu }{l^2}\kappa u-u^2}}}}$

Tenemos que resolver una integral del tipo

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{-du}{\sqrt{-u^2+2bu+c}}}={\displaystyle \int \frac{-du}{\sqrt{c+b^2-{\left(u-b\right)}^2}}}\hfill \\ b=\frac{\mu }{l^2}\kappa ,c=\frac{2\mu }{l^2}E\hfill \end{array}}$

Efectuamos un nuevo cambio de variable, z=u-b, dz=du

${\displaystyle -{\displaystyle \int \frac{dz}{\sqrt{c+b^2-z^2}}}=-\arcsin \frac{z}{\sqrt{c+b^2}}-C}$

Donde C es una constante de integración que determinaremos más adelante

Deshacemos los cambios

${\displaystyle \begin{array}{l}\theta =-\arcsin \frac{u-b}{\sqrt{c+b^2}}-C\\ \frac{1}{r}-b=\sqrt{c+b^2}\sin \left(-C-\theta \right)\\ \frac{1}{r}-b=-\sqrt{c+b^2}\sin \left(C+\theta \right)\end{array}}$

Tomando C=-π/2, sin(θ-π/2)=-cos(θ),

${\displaystyle \begin{array}{l}\frac{1}{r}-b=\sqrt{c+b^2}\cos \theta \\ r=\frac{1}{\cos \theta \sqrt{c+b^2}+b}\\ r=\frac{1}{\cos \theta \sqrt{\frac{2\mu }{l^2}E+\frac{{\mu }^2{\kappa }^2}{l^4}}+\frac{\mu \kappa }{l^2}}\\ r=\frac{1}{\frac{\mu \kappa }{l^2}\left(\cos \theta \sqrt{1+\frac{2l^{2}E}{\mu {\kappa }^2}}+1\right)}=\frac{d}{1+\epsilon \cos \theta },\{\begin{array}{l}d=\frac{l^2}{\mu \kappa }\\ \epsilon =\sqrt{1+\frac{2l^{2}E}{\mu {\kappa }^2}}\end{array}\end{array}}$

La trayectoria es una elipse con ε<1. La energía E es negativa

Tomando el valor de la constante C=-π/2, establecemos el origen de ángulos, el ángulo θ=0, cuando la distancia r es mínima

Geometría de la elipse

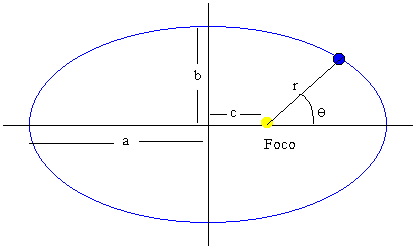
El eje mayor 2a de la elipse es la suma de la distancia mínima (θ=0) y máxima (θ=π) al centro de fuerzas situado en el foco de la elipse

${\displaystyle \begin{array}{l}2a=\frac{d}{1+\epsilon }+\frac{d}{1-\epsilon }\\ a=\frac{d}{1-{\epsilon }^2}\end{array}}$

La excentricidad de la elipse es el cociente ε=c/a

La semidistancia focal c es

${\displaystyle c=a-\frac{d}{1+\epsilon }=\frac{d}{1-{\epsilon }^2}-\frac{d}{1+\epsilon }=\frac{d}{1-{\epsilon }^2}\epsilon }$

El semieje menor b es

${\displaystyle b^2=a^2-c^2=\frac{d^2}{1-{\epsilon }^2},b=\frac{d}{\sqrt{1-{\epsilon }^2}}}$

Sabiendo que el parámetro d=b²/a, otra forma de expresar la ecuación de la elipse es

${\displaystyle r=\frac{b^2}{a\left(1+\epsilon \cos \theta \right)}}$

La energía E de la partícula solamente depende del semieje mayor a de la elipse

${\displaystyle \begin{array}{l}a=\frac{d}{1-{\epsilon }^2}\\ \{\begin{array}{l}d=\frac{l^2}{\mu \kappa }\\ \epsilon =\sqrt{1+\frac{2l^{2}E}{\mu {\kappa }^2}}\end{array}\\ E=-\frac{\kappa }{2a}\end{array}}$

Reglas de cuantización

• Angular

${\displaystyle \begin{array}{l}{\displaystyle \oint p_{\theta }d\theta }=n_{\theta }h\\ p_{\theta }=\frac{\partial L}{\partial \dot{\theta }}=\mu r^2\frac{d\theta }{dt}=l\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}l·d\theta =n_{\theta }h}\\ 2\pi l=n_{\theta }h,n_{\theta }=\mathrm{1,2,3...}\end{array}}$

• Radial

${\displaystyle \begin{array}{l}{\displaystyle \oint p_{r}dr}=n_{r}h\\ p_r=\frac{\partial L}{\partial \dot{r}}=\mu \frac{dr}{dt}=\mu \frac{dr}{d\theta }\frac{d\theta }{dt}=\mu \frac{dr}{d\theta }\frac{l}{\mu r^2}=\frac{l}{r^2}\frac{dr}{d\theta }\\ {\displaystyle \oint p_{r}dr}={\displaystyle \oint \frac{l}{r^2}\frac{dr}{d\theta }dr}={\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{l}{r^2}{\left(\frac{dr}{d\theta }\right)}^{2}d\theta }\\ \frac{dr}{d\theta }=-\frac{b^2}{a}\frac{\epsilon \sin \theta }{{\left(1+\epsilon \cos \theta \right)}^2}\\ {\displaystyle \oint p_{r}dr}=l{\epsilon }^2{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{{\sin }^2\theta }{{\left(1+\epsilon \cos \theta \right)}^2}d\theta }\end{array}}$

Resolvemos la integral. Sea

${\displaystyle \begin{array}{l}z=1+\epsilon \cos \theta ,dz=-\epsilon \sin \theta ·d\theta \\ -\frac{1}{\epsilon }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\sin \theta }{z^2}dz}\end{array}}$

Integramos por partes

${\displaystyle \begin{array}{l}-\frac{1}{\epsilon }{\displaystyle \int \frac{\sin \theta }{z^2}dz},\{\begin{array}{l}u=\sin \theta ,du=\cos \theta ·d\theta \\ dv=\frac{dz}{z^2},v=-\frac{1}{z}\end{array}\\ -\frac{1}{\epsilon }{\displaystyle \int \frac{\sin \theta }{z^2}dz}=-\frac{1}{\epsilon }\left\{-\frac{\sin \theta }{z}+{\displaystyle \int \frac{\cos \theta ·d\theta }{z}}\right\}=-\frac{1}{\epsilon }\left\{-\frac{\sin \theta }{1+\epsilon \cos \theta }+{\displaystyle \int \frac{\cos \theta ·d\theta }{1+\epsilon \cos \theta }}\right\}\\ {\displaystyle \oint p_{r}dr}=-l{\epsilon }^2\frac{1}{\epsilon }\left\{{-\frac{\sin \theta }{1+\epsilon \cos \theta }|}_0^{2\pi }+{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\cos \theta ·d\theta }{1+\epsilon \cos \theta }}\right\}=-l\epsilon {\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\cos \theta ·d\theta }{1+\epsilon \cos \theta }}\end{array}}$

En el numerador, sumamos y restamos la unidad

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\cos \theta }{1+\epsilon \cos \theta }d\theta }=\frac{1}{\epsilon }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\epsilon \cos \theta }{1+\epsilon \cos \theta }d\theta }=\frac{1}{\epsilon }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{1+\epsilon \cos \theta -1}{1+\epsilon \cos \theta }d\theta }=\\ \frac{1}{\epsilon }\left\{{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\theta }-{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{1}{1+\epsilon \cos \theta }d\theta }\right\}=\frac{1}{\epsilon }\left\{2\pi -2{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{1}{1+\epsilon \cos \theta }d\theta }\right\}\end{array}}$

Llegamos a este resultado

${\displaystyle {\displaystyle \oint p_{r}dr}=-l\epsilon \frac{1}{\epsilon }\left\{2\pi -2{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{1}{1+\epsilon \cos \theta }d\theta }\right\}=-2l\left\{\pi -{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{1}{1+\epsilon \cos \theta }d\theta }\right\}}$

Pra resolver la integral, hacemos el cambio de variable

${\displaystyle x=\tan \frac{\theta }{2},dx=\frac{1}{2}\frac{1}{{\cos }^2\frac{\theta }{2}}d\theta }$

Utilizamos las relaciones trigonométricas

${\displaystyle \begin{array}{l}{\sin }^2\frac{\theta }{2}=\frac{{\tan }^2\frac{\theta }{2}}{1+{\tan }^2\frac{\theta }{2}}=\frac{x^2}{1+x^2},{\cos }^2\frac{\theta }{2}=\frac{1}{1+{\tan }^2\frac{\theta }{2}}=\frac{1}{1+x^2}\\ \cos \theta ={\cos }^2\frac{\theta }{2}-{\sin }^2\frac{\theta }{2}=\frac{1-x^2}{1+x^2}\end{array}}$

Integramos respecto de x ente los límites 0 e ∞

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{1}{1+\epsilon \cos \theta }d\theta }={\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1}{1+\epsilon \frac{1-x^2}{1+x^2}}\frac{2}{1+x^2}dx}=2{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{dx}{1+\epsilon +x^2\left(1-\epsilon \right)}}=\\ \frac{2}{1-\epsilon }{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{dx}{\frac{1+\epsilon }{1-\epsilon }+x^2}}={\frac{2}{1-\epsilon }\frac{1}{\sqrt{\frac{1+\epsilon }{1-\epsilon }}}\arctan \left(\frac{x}{\sqrt{\frac{1+\epsilon }{1-\epsilon }}}\right)|}_0^{\infty }=\frac{2}{\sqrt{1-{\epsilon }^2}}\left(\frac{\pi }{2}-0\right)=\frac{\pi }{\sqrt{1-{\epsilon }^2}}\end{array}}$

El resultado final es

${\displaystyle \begin{array}{l}{\displaystyle \oint p_{r}dr}=-2l\left\{\pi -{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{1}{1+\epsilon \cos \theta }d\theta }\right\}=-2l\left\{\pi -\frac{\pi }{\sqrt{1-{\epsilon }^2}}\right\}=2\pi l\left(\frac{1}{\sqrt{1-{\epsilon }^2}}-1\right)\\ {\displaystyle \oint p_{r}dr}=2\pi l\left(\frac{a}{b}-1\right)=n_{r}h,n_r=\mathrm{0,1,2,3,...}\end{array}}$

Niveles de energía

En el apartado anterior, hemos obtenido los siguientes resultados

${\displaystyle \begin{array}{l}\{\begin{array}{l}2\pi l=n_{\theta }h,n_{\theta }=\mathrm{1,2,3...}\\ 2\pi l\left(\frac{a}{b}-1\right)=n_{r}h,n_r=\mathrm{0,1,2,3,...}\end{array}\\ n_{\theta }\left(\frac{a}{b}-1\right)=n_r\\ \frac{b}{a}=\frac{n_{\theta }}{n_{\theta }+n_r}\\ \sqrt{1-{\epsilon }^2}=\frac{n_{\theta }}{n_{\theta }+n_r}\end{array}}$

Para n_r=0, la órbita es circular

Niveles de energía

${\displaystyle \begin{array}{l}E=-\frac{\kappa }{2a}\\ a=\frac{\frac{l^2}{\mu \kappa }}{1-{\epsilon }^2}=\frac{l^2}{\mu \kappa \left(1-{\epsilon }^2\right)}\\ E=-\frac{\mu {\kappa }^2\left(1-{\epsilon }^2\right)}{2l^2}=-\frac{\mu {\kappa }^2}{2l^2}{\left(\frac{n_{\theta }}{n_{\theta }+n_r}\right)}^2\\ 2\pi l=n_{\theta }h,l=n_{\theta }\hslash \\ E=-\frac{\mu {\kappa }^2}{2n_{\theta }^2{\hslash }^2}{\left(\frac{n_{\theta }}{n_{\theta }+n_r}\right)}^2=-\frac{\mu {\kappa }^2}{2{\hslash }^2{\left(n_{\theta }+n_r\right)}^2}\\ E=-\frac{\mu Z^2{q}^2}{8h^2{\epsilon }_0^2{\left(n_{\theta }+n_r\right)}^2}\end{array}}$

Donde q=e es la carga del electrón. La masa del núcleo es mucho mayor que la masa del electrón por lo que μ≈m_e. Obtenemos la fórmula de Bohr con n=n_r+n_θ

Orbitas para n_r+n_θ=4

El semeje mayor de la elipse a vale

${\displaystyle a=\frac{{\hslash }^2{\left(n_{\theta }+n_r\right)}^2}{\mu \kappa }}$

La ecuación de la elipse es

${\displaystyle \begin{array}{l}r=\frac{b^2}{a\left(1+\epsilon \cos \theta \right)}\\ \frac{b}{a}=\frac{n_{\theta }}{n_{\theta }+n_r}\\ \sqrt{1-{\epsilon }^2}=\frac{n_{\theta }}{n_{\theta }+n_r}\end{array}}$

Expresamos la ecuación de la elipse en términos de los números n_r y n_θ

${\displaystyle r=\frac{{\left(\frac{n_{\theta }}{n_{\theta }+n_r}\right)}^2\frac{{\hslash }^2{\left(n_{\theta }+n_r\right)}^2}{\mu \kappa }}{1+\sqrt{1-{\left(\frac{n_{\theta }}{n_{\theta }+n_r}\right)}^2}\cos \theta }=\frac{n_{\theta }^2}{1+\sqrt{1-{\left(\frac{n_{\theta }}{n_{\theta }+n_r}\right)}^2}\cos \theta }\frac{{\hslash }^2}{\mu \kappa }}$

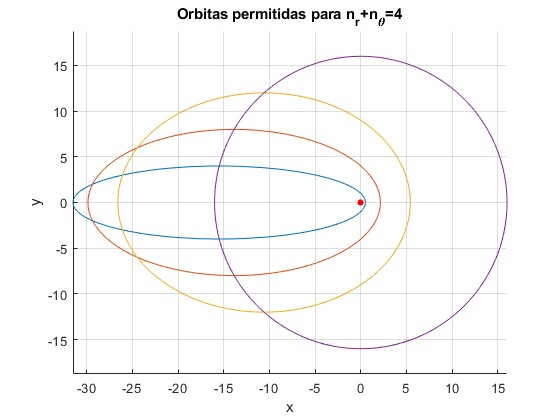
Representamos las órbitas permitidas para n_r+n_θ=4. El punto de color rojo, representa el centro de masas. La órbita circular corresponde a n_r=0, n_θ=4

n=4;
hold on
for n_t=1:n
    r=@(x) n_t^2./(1+sqrt(1-n_t^2/n^2)*cos(x));
    fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0,2*pi])
end
plot(0,0,'ro','markersize',4,'markerfacecolor','r') %núcleo
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('Orbitas permitidas para n_r+n_\theta=4')

Referencias

Blomm D., Blomm D. W. Vibrating wire loop and the Bohr model. The Physics Teacher, 41, May 2003, pp. 292-294

Wilder R. Cardoso, Mariana C. Nakagaki. Revisiting Sommerfeld’s atomic model using Euler–Lagrange dynamics. Am. J. Phys. 92 (11), November 2024. pp. 872-877