Choques en una dimensión

En esta página se describen los choques de dos partículas en una dimensión.

En un sistema aislado de dos patículas interactuantes, se conserva el momento lineal

El balance energético de la colisión se sustituye por el concepto de coeficente de restitución. Un diagrama en forma de tarta nos muestra como se transforma la energía inicial del sistema de dos partículas tras el choque

Se describe tambén el choque entre las dos partículas en un Sistema de Referencia que viaja con el centro de masa (c.m.). En un sistema aislado el c.m. se mueve con velocidad constante. El lector puede así comparar las descripciones de un mismo fenómeno desde dos puntos de vista diferentes

Al final de la página, se resuelve un problema que estudia los sucesivos choques elásticos entre dos partículas que se mueven a lo largo de un plano inclinado

En esta página, se describen los choques frontales de dos partículas en el Sistema de Referencia del Laboratorio (Sistema -L) y en el Sistema de Referencia del Centro de Masa (Sistema–C).

Coeficiente de restitución

Se ha encontrado experimentalmente que en una colisión frontal de dos esferas sólidas como las que experimentan las bolas de billar, las velocidades después del choque están relacionadas con las velocidades antes del choque, por la expresión

$v_{1} - v_{2} = - e (u_{1} - u_{2})$

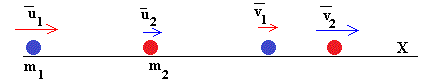
donde e es el coeficiente de restitución y tiene un valor entre 0 y 1. Esta relación fue propuesta por Newton y tiene validez solamente aproximada. El valor de uno es para un choque perfectamente elástico y el valor de cero para un choque perfectamente inelástico.

Choques frontales

Descripción desde el Sistema de Referencia del Laboratorio

Supongamos que la segunda partícula u₂=0, está en reposo antes del choque. La conservación de la conservación del momento lineal

m₁u₁+m₂u₂=m₁v₁+m₂v₂

De la definición del coeficiente de restitución e

-e(u₁-u₂)=v₁-v₂

Despejando las velocidades después del choque v₁ y v₂

$v_{1} = \frac{(m_{1} - m_{2} e) u_{1} + m_{2} (1 + e) u_{2}}{m_{1} + m_{2}} v_{2} = \frac{m_{1} (1 + e) u_{1} + (m_{2} - m_{1} e) u_{2}}{m_{1} + m_{2}}$

La velocidad v₁ después del choque, de la partícula de masa m₁ es más pequeña que la velocidad v₂ después del choque, de la partícula de masa m₂

Supongamos que v₁<v₂

$\begin{array}{l} (m_{1} - m_{2} e) u_{1} + m_{2} (1 + e) u_{2} < m_{1} (1 + e) u_{1} + (m_{2} - m_{1} e) u_{2} \\ m_{2} (u_{2} - u_{1}) < m_{1} (u_{1} - u_{2}) \end{array}$

Para que se produzca choque, las velocidades iniciales, antes del choque, u₁>u₂. A la izquierda tenemos un número negativo y a la derecha un número positivo, por lo que es una afirmación correcta

Teniendo en cuenta que la velocidad del centro de masas es

$V_{c m} = \frac{m_{1} u_{1} + m_{2} u_{2}}{m_{1} + m_{2}}$

Escribimos las expresiones de la velocidad de las partículas después del choque v₁ y v₂ de forma más simplificada.

v₁=(1+e)V_cm-eu₁v₂=(1+e)V_cm-eu₂

Si la segunda partícula está en reposo antes del choque, u₂=0. Las velocidades después del choque v₁ y v₂ serán.

$v_{1} = \frac{m_{1} - e m_{2}}{m_{1} + m_{2}} u_{1} v_{2} = \frac{m_{1} (1 + e)}{m_{1} + m_{2}} u_{1}$

Descripción desde el Sistema de Referencia del Centro de Masa

Velocidad de las partículas respecto del Sistema-C antes del choque

$\begin{array}{l} u_{1 c m} = u_{1} - V_{c m} = \frac{m_{2}}{m_{1} + m_{2}} (u_{1} - u_{2}) \\ u_{2 c m} = u_{2} - V_{c m} = - \frac{m_{1}}{m_{1} + m_{2}} (u_{1} - u_{2}) \end{array}$

Velocidad de las partículas respecto del Sistema-C después del choque

$\begin{array}{l} v_{1 c m} = v_{1} - V_{c m} = - \frac{m_{2} e}{m_{1} + m_{2}} (u_{1} - u_{2}) \\ v_{2 c m} = v_{2} - V_{c m} = \frac{m_{1} e}{m_{1} + m_{2}} (u_{1} - u_{2}) \end{array}$

v_1cm=-e·u_1cmv_2cm=-e·u_2cm

La velocidad de ambos objetos después del choque en el Sistema-C se reducen en un factor e.

Comprobamos también que se cumple el principio de conservación del momento lineal en el Sistema-C

m₁·u_1cm+m₂·u_2cm=0
m₁·v_1cm+m₂·v_2cm=0

Energía perdida en el choque

La energía perdida en la colisión Q es la diferencia de las energías cinéticas después del choque y antes del choque en el Sistema-L.

$Q = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2} - \frac{1}{2} m_{1} u_{1}^{2} - \frac{1}{2} m_{2} u_{2}^{2}$

Pero es mucho más fácil calcular esta diferencia en el Sistema-C.

$Q = - \frac{1}{2} (1 - e^{2}) \frac{m_{1} m_{2}}{m_{1} + m_{2}} {(u_{1} - u_{2})}^{2}$

Ejemplo:

Primera partícula: m₁=1, u₁=2
Segunda partícula: m₂=2, u₂=0
Coeficiente de restitución: e=0.9

Principio de conservación del momento lineal

1·2+2·0=1·v₁+2·v₂

Definición de coeficiente de restitución

-0.9(2-0)=v₁-v₂

Resolviendo el sistema de dos ecuaciones con dos incógnitas obtenemos

v₁=-0.53, v₂=1.27 m/s

Energía perdida en la colisión (Sistema-L)

$Q = \frac{1}{2} 1 \cdot {0.53}^{2} + \frac{1}{2} 2 \cdot {1.27}^{2} - \frac{1}{2} 1 \cdot 2^{2} = - 0.253 J$

Calculada mediante la fórmula (Sistema-C)

$Q = - \frac{1}{2} (1 - {0.9}^{2}) \frac{1 \cdot 2}{1 + 2} {(2 - 0)}^{2} = - 0.253 J$

Solución con MATLAB

%masas y velocidades iniciales de las partículas
m1=1;
u1=2;
m2=2;
u2=0;
e=0.9; %coeficiente de restitución
%velocidades después del choque
v1=((m1-m2*e)*u1+m2*(1+e)*u2)/(m1+m2);
v2=(m1*(1+e)*u1+(m2-m1*e)*u2)/(m1+m2);
fprintf('Velocidades: %1.2f de la partícula 1, 
%1.2f de la partícula 2\n',v1,v2);
Q=0.5*(1-e^2)*m1*m2*(u1-u2)^2/(m1+m2);
labels = {'Ek partícula 1','Ek partícula 2','Energía perdida'}
X=[m1*v1^2/2,m2*v2^2/2,Q];
pie(X,labels)

Velocidades: -0.53 de la partícula 1, 1.27 de la partícula 2

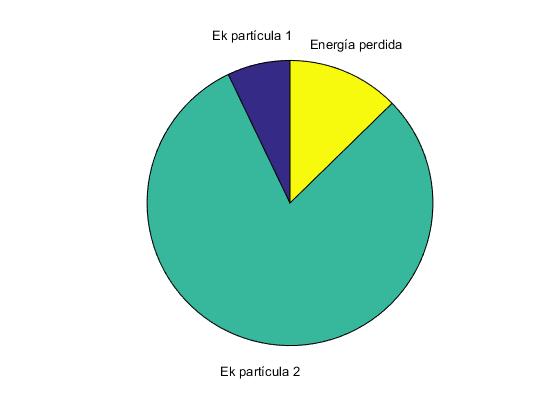
En el diagrama de tarta vemos como se reparte la energía inicial del sistema de dos partículas: Energía cinética de la primera partícula, energía cinética de la segunda partícula, energía Q perdida en el choque

Choques elásticos

Obtenemos de forma alternativa, las velocidades v₁ y v₂ después del choque para un choque elástico empleando la conservación del momento lineal y de la energía cinética.

Principio de conservación del momento lineal

m₁u₁+m₂u₂=m₁v₁+m₂v₂

En un choque elástico, la energía cinética inicial es igual a la final, Q=0.

$\frac{1}{2} m_{1} u_{1}^{2} + \frac{1}{2} m_{2} u_{2}^{2} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2}$

Dados u₁ y u₂, las velocidades de las partículas m₁ y m₂ antes del choque, calculamos las velocidades de las partículas v₁ y v₂ después del choque resolviendo el sistema de dos ecuaciones con dos incógnitas.

Trasformamos las dos ecuaciones, en las equivalentes

$\begin{array}{l} m_{1} (u_{1} - v_{1}) = - m_{2} (u_{2} - v_{2}) \\ m_{1} (u_{1}^{2} - v_{1}^{2}) = - m_{2} (u_{2}^{2} - v_{2}^{2}) \end{array}$

La diferencia de los cuadrados de dos números es igual al producto de su suma por su diferencia

$\begin{array}{l} m_{1} (u_{1} - v_{1}) = - m_{2} (u_{2} - v_{2}) \\ m_{1} (u_{1} - v_{1}) (u_{1} + v_{1}) = - m_{2} (u_{2} - v_{2}) (u_{2} + v_{2}) \end{array}$

Nos queda un sistema de dos ecuaciones más fácil de resolver

$\begin{array}{l} m_{1} (u_{1} - v_{1}) = - m_{2} (u_{2} - v_{2}) \\ (u_{1} + v_{1}) = (u_{2} + v_{2}) \end{array}$

Despejamos las velocidades de las partículas después del choque v₁ y v₂

$v_{1} = \frac{2 m_{2} u_{2} + (m_{1} - m_{2}) u_{1}}{m_{1} + m_{2}} v_{2} = \frac{2 m_{1} u_{1} + (m_{2} - m_{1}) u_{2}}{m_{1} + m_{2}}$

Son las mismas ecuaciones que hemos obtenido previamente con el coeficiente de restitución e=1.

El caso particular mas interesante ocurre cuando las masas de las dos partículas son iguales, m₁=m₂ y la segunda partícula está inicialmente en reposo u₂=0. Después del choque, la primera partícula queda en reposo v₁=0 y la velocidad de la segunda partícula v₂=u₁. La energía cinética de la primera particula se transfiere integramente a la segunda

Teniendo en cuenta que la velocidad del centro de masas es

$V_{c m} = \frac{m_{1} u_{1} + m_{2} u_{2}}{m_{1} + m_{2}}$

Escribimos las expresiones de la velocidad de las partículas después del choque v₁ y v₂ de forma más simplificada.

v₁=2V_cm-u₁v₂=2V_cm-u₂

Choque completamente inelásticos

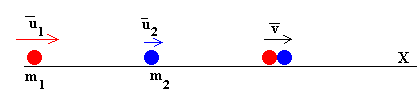
Las partículas quedan pegadas después del choque moviéndose con la misma velocidad v₁=v₂=v

Principio de conservación del momento lineal

m₁u₁+m₂u₂=(m₁+m₂)v

En un choque inelástico, la energía cinética inicial es mayor que la final

$\begin{array}{l} \frac{1}{2} m_{1} u_{1}^{2} + \frac{1}{2} m_{2} u_{2}^{2} + Q = \frac{1}{2} (m_{1} + m_{2}) v^{2} \\ Q = - \frac{1}{2} \frac{m_{1} m_{2}}{m_{1} + m_{2}} {(u_{1} - u_{2})}^{2} \end{array}$

Los mismos resultados que hemos obtenido para los choques frontales con el coeficiente de restitución e=0

Definimos la razón f al cociente entre energía cinética final e inicial

$\begin{array}{l} f = \frac{\frac{1}{2} (m_{1} + m_{2}) v^{2}}{\frac{1}{2} m_{1} u_{1}^{2} + \frac{1}{2} m_{2} u_{2}^{2}} = \frac{{(m_{1} u_{1} + m_{2} u_{2})}^{2}}{(m_{1} + m_{2}) (m_{1} u_{1}^{2} + m_{2} u_{2}^{2})} \\ f = \frac{{(1 + m x)}^{2}}{(1 + m) (1 + m x^{2})}, x = \frac{u_{2}}{u_{1}}, m = \frac{m_{2}}{m_{1}} \end{array}$

Para que se produzca un choque

u₁>0 y u₁>u₂, 0<x<1
Choque frontal, u₁>0 y u₂<0, -∞<x<0

Representamos f en función de x para tres valores de m=1/3, 1, 3.

hold on
for m=[1/3,1,3]
    f=@(x) ((1+m*x).^2)./((1+m)*(1+m*x.^2));
    fplot(f,[-10,1])
end
xlabel('u_2/u_1')
ylabel('f')
grid on
legend('m=1/3','m=1','m=3', 'Location','best')
title('Fracción de energía cinética')

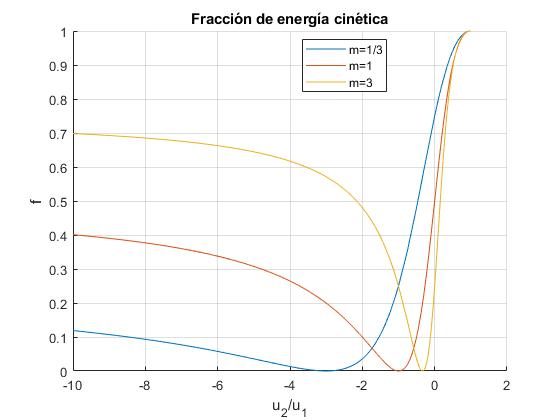
f=0, en una colisión es frontal en la que v=0, m₁u₁+m₂u₂=0, es decir, para x=-1/m
f=1, cuando u₁=u₂. En realidad, las partículas no llegan a chocar
Cuando la segunda partícula está en reposo, u₂=0, x=0, la fracción f=1/(1+m).
Cuando x→-∞ (por ejemplo, la primera partícula está en reposo u₁=0 y u₂<0). f tiende hacia un valor constante m/(1+m). Por ejemplo, para m=1/3, f→1/4

Actividades

Se introduce

El coeficiente de restitución e, un valor comprendido entre 0 y 1en el control titulado Coef. restitución. El valor de 1 corresponde a un choque elástico
El cociente entre las masas m₂/m₁, en el control titulado Cociente masas. Donde m₂ es la masa de la partícula que está inicialmente en reposo y m₁ la masa de la partícula inicialmente en movimiento.
La velocidad de la primera partícula u₁, en el control titulado Velocidad

Se pulsa el botón titulado Nuevo.

En la mitad superior del programa interactivo, se representa el choque frontal en el Sistema-L del laboratorio. Una cruz de color rosa representa la posición del centro de masas del sistema formado por las dos partículas interactuantes. Se representa también mediante un diagrama de tarta la energía inicial y final de las partículas. Cuando el choque es elástico la energía inicial es igual a la final. Cuando el choque es inelástico (coeficiente de restitución menor que la unidad) la energía final es menor que la inicial.

En la parte inferior, se representa el mismo choque en el Sistema-C del centro de masas

Se proporcionan los datos correspondientes a la velocidad de las partículas antes del choque y después del choque tanto en el Sistema–L como en el Sistema-C. Se representan también los momentos lineales en forma de vectores antes del choque y después del choque. De este modo el lector puede comprobar de forma visual la conservación del momento lineal.

Velocidad (m/s) Cociente masas (m₂/m₁)
Coef. restitución:

Ejemplo

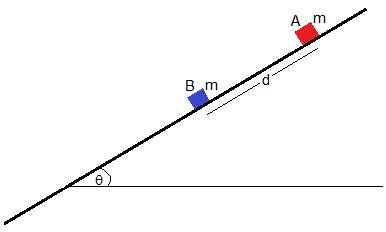
Dos cuerpos A y B de la misma masa m se sitúan en un plano inclinado θ muy largo, con A por encima de B separados una distancia d.

El coeficiente cinético de rozamiento entre el cuerpo A y el plano inclinado es μ_A
El coeficiente cinético de rozamiento entre el cuerpo B y el plano inclinado es μ_B

Se cumple que tan θ>μ_B>μ_A.

Los cuerpos se sueltan en el instante t=0.

¿En qué instante t₁, los cuerpos chocan por primera vez?
¿En que otros instantes, los cuerpos vuelven a chocar?
Representar la velocidad y posición de cada uno de los cuerpos en función del tiempo

Choque elástico

Sea un choque elástico, coeficiente de restitución e=1, entre dos partículas de la misma masa, m₁=m₂=m. Se resuelve el sistema de dos ecuaciones

${\begin{cases} u_{1} + u_{2} = v_{1} + v_{2} \\ - (u_{1} - u_{2}) = v_{1} - v_{2} \end{cases}$

Las velocidades iniciales, justo antes del choque son u₁ y u₂ y las velocidades finales, justo después del choque, v₁ y v₂

Alternativamente, de la conservación del momento lineal y la energía

${\begin{cases} u_{1} + u_{2} = v_{1} + v_{2} \\ \frac{1}{2} u_{1}^{2} + \frac{1}{2} u_{2}^{2} = \frac{1}{2} v_{1}^{2} + \frac{1}{2} v_{2}^{2} \end{cases}$

El resultado es v₁=u₂, v₂=u₁. Se intercambian las velocidades de las dos partículas

Etapa inicial

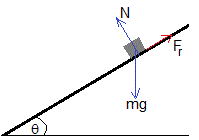
La condición tanθ>μ, implica que mg·sinθ>μmg·cosθ, el cuerpo desliza a lo largo del plano inclinado. Las ecuaciones del movimiento son

$\begin{array}{l} {\begin{cases} N = m g \cos θ \\ m a = m g \sin θ - F_{r} \end{cases} \\ F_{r} = μ N = μ m g \cos θ \\ a = g (\sin θ - μ \cos θ) \end{array}$

Las aceleraciones de cada uno de los cuerpos son

$\begin{array}{l} {\begin{cases} a_{A} = g (\sin θ - μ_{A} \cos θ) \\ a_{B} = g (\sin θ - μ_{B} \cos θ) \end{cases} \\ μ_{A} < μ_{B}, a_{A} > a_{B} \end{array}$

En la etapa inicial, el cuerpo A desliza y alcanza el cuerpo B con el que choca. Ponemos el origen en la posición inicial del cuerpo A, de modo que, en el instante t=0, x_A=0 y x_B=d, parten del reposo. En el instante t

$A {\begin{cases} v = a_{A} t \\ x = \frac{1}{2} a_{A} t^{2} \end{cases} B {\begin{cases} v = a_{B} t \\ x = d + \frac{1}{2} a_{B} t^{2} \end{cases}$

Se encuentran en el instante t₁, cuando x_A=x_B

$\begin{array}{l} \frac{1}{2} a_{A} t^{2} = d + \frac{1}{2} a_{B} t^{2} \\ t_{1} = \sqrt{\frac{2 d}{a_{A} - a_{B}}} = \sqrt{\frac{2 d}{g (μ_{B} - μ_{A}) \cos θ}} \end{array}$

La posición de encuentro es

$x_{1} = \frac{1}{2} a_{A} t_{1}^{2} = \frac{1}{2} g (\sin θ - μ_{A} \cos θ) t_{1}^{2}$

En el instante t₁ los cuerpos van a chocar, sus velocidades inmediatamente antes del choque son

${\begin{cases} u_{A} = g (\sin θ - μ_{A} \cos θ) t_{1} \\ u_{B} = g (\sin θ - μ_{B} \cos θ) t_{1} \end{cases}$

Primera etapa

Las velocidades después del choque, iniciales para la primera etapa del movimiento son

$\begin{array}{l} {\begin{cases} v_{0 A} = u_{B} = g (\sin θ - μ_{B} \cos θ) t_{1} \\ v_{0 B} = u_{A} = g (\sin θ - μ_{A} \cos θ) t_{1} \end{cases} \\ v_{0 A} < v_{0 B} \end{array}$

La velocidad inicial de A es menor que la de B pero la aceleración de A es mayor que la de B luego, se volverán a encontrar

La velocidad y la posición en el instante t de cada uno de los cuerpos

$A {\begin{cases} v = v_{0 A} + a_{A} t \\ x = x_{1} + v_{0 A} t + \frac{1}{2} a_{A} t^{2} \end{cases} B {\begin{cases} v = v_{0 B} + a_{B} t \\ x = x_{1} + v_{0 B} t + \frac{1}{2} a_{B} t^{2} \end{cases}$

Se encuentran en el instante t₁+t₂. Calculamos t₂ haciendo x_A=x_B

$\begin{array}{l} x_{1} + v_{0 A} t + \frac{1}{2} a_{A} t^{2} = x_{1} + v_{0 B} t + \frac{1}{2} a_{B} t^{2} \\ t_{2} = \frac{2 (v_{0 B} - v_{0 A})}{a_{A} - a_{B}} = 2 t_{1} \end{array}$

La posición de encuentro es

$\begin{array}{l} x_{2} = x_{1} + v_{0 A} t_{2} + \frac{1}{2} a_{A} t_{2}^{2} = \frac{1}{2} g (\sin θ - μ_{A} \cos θ) t_{1}^{2} + g (\sin θ - μ_{B} \cos θ) t_{1} \cdot 2 t_{1} + \frac{1}{2} g (\sin θ - μ_{A} \cos θ) {(2 t_{1})}^{2} \\ x_{2} = \frac{1}{2} g (9 \sin θ - (5 μ_{A} + 4 μ_{B}) \cos θ) t_{1}^{2} \end{array}$

Las velocidades de los dos cuerpos, en el instante 3t₁, antes del choque, son

${\begin{cases} u_{A} = v_{0 A} + a_{A} t_{2} = a_{B} t_{1} + a_{A} t_{2} = g (3 \sin θ - (μ_{B} + 2 μ_{A}) \cos θ) t_{1} \\ u_{B} = v_{0 B} + a_{B} t_{2} = a_{A} t_{1} + a_{B} t_{2} = g (3 \sin θ - (μ_{A} + 2 μ_{B}) \cos θ) t_{1} \end{cases}$

Segunda etapa

Las velocidades después del choque, iniciales para la segunda etapa del movimiento son

${\begin{cases} v_{0 A} = u_{B} = g (3 \sin θ - (μ_{A} + 2 μ_{B}) \cos θ) t_{1} \\ v_{0 B} = u_{A} = g (3 \sin θ - (μ_{B} + 2 μ_{A}) \cos θ) t_{1} \end{cases}$

La velocidad y la posición en el instante t de cada uno de los cuerpos

$A {\begin{cases} v = v_{0 A} + a_{A} t \\ x = x_{2} + v_{0 A} t + \frac{1}{2} a_{A} t^{2} \end{cases} B {\begin{cases} v = v_{0 B} + a_{B} t \\ x = x_{2} + v_{0 B} t + \frac{1}{2} a_{B} t^{2} \end{cases}$

Se encuentran en el instante 3t₁+t₃. Calculamos t₃ haciendo x_A=x_B

$\begin{array}{l} x_{2} + v_{0 A} t_{3} + \frac{1}{2} a_{A} t_{3}^{2} = x_{2} + v_{0 B} t_{3} + \frac{1}{2} a_{B} t_{3}^{2} \\ t_{3} = \frac{2 (v_{0 B} - v_{0 A})}{a_{A} - a_{B}} = 2 t_{1} \end{array}$

La posición de encuentro es

$\begin{array}{l} x_{3} = x_{2} + v_{0 A} t_{3} + \frac{1}{2} a_{A} t_{3}^{2} \\ x_{3} = \frac{1}{2} g (9 \sin θ - (5 μ_{A} + 4 μ_{B}) \cos θ) t_{1}^{2} + g (3 \sin θ - (μ_{A} + 2 μ_{B}) \cos θ) t_{1} (2 t_{1}) + \frac{1}{2} g (\sin θ - μ_{A} \cos θ) {(2 t_{1})}^{2} \\ x_{3} = \frac{1}{2} g (25 \sin θ - (13 μ_{A} + 12 μ_{B}) \cos θ) t_{1}^{2} \end{array}$

Las velocidades de los dos cuerpos, en el instante 5t₁, antes del choque, son

$\begin{array}{l} {\begin{cases} u_{A} = v_{0 A} + a_{A} t_{3} \\ u_{B} = v_{0 B} + a_{B} t_{3} \end{cases} \\ {\begin{cases} u_{A} = g (3 \sin θ - (μ_{A} + 2 μ_{B}) \cos θ) t_{1} + g (\sin θ - μ_{A} \cos θ) (2 t_{1}) = g (5 \sin θ - (3 μ_{A} + 2 μ_{B}) \cos θ) t_{1} \\ u_{B} = g (3 \sin θ - (μ_{B} + 2 μ_{A}) \cos θ) t_{1} + g (\sin θ - μ_{B} \cos θ) (2 t_{1}) = g (5 \sin θ - (2 μ_{A} + 3 μ_{B}) \cos θ) t_{1} \end{cases} \end{array}$

Tercera etapa

Las velocidades después del choque, iniciales para la tercera etapa del movimiento son

${\begin{cases} v_{0 A} = u_{B} = g (5 \sin θ - (2 μ_{A} + 3 μ_{B}) \cos θ) t_{1} \\ v_{0 B} = u_{A} = g (5 \sin θ - (2 μ_{B} + 3 μ_{A}) \cos θ) t_{1} \end{cases}$

La velocidad y la posición en el instante t de cada uno de los cuerpos

$A {\begin{cases} v = v_{0 A} + a_{A} t \\ x = x_{3} + v_{0 A} t + \frac{1}{2} a_{A} t^{2} \end{cases} B {\begin{cases} v = v_{0 B} + a_{B} t \\ x = x_{3} + v_{0 B} t + \frac{1}{2} a_{B} t^{2} \end{cases}$

Se encuentran en el instante 5t₁+t₄. Calculamos t₄ haciendo x_A=x_B

$\begin{array}{l} x_{3} + v_{0 A} t_{4} + \frac{1}{2} a_{A} t_{4}^{2} = x_{3} + v_{0 B} t_{4} + \frac{1}{2} a_{B} t_{4}^{2} \\ t_{4} = \frac{2 (v_{0 B} - v_{0 A})}{a_{A} - a_{B}} = 2 t_{1} \end{array}$

La posición de encuentro es

$\begin{array}{l} x_{4} = x_{3} + v_{0 A} t_{4} + \frac{1}{2} a_{A} t_{4}^{2} \\ x_{4} = \frac{1}{2} g (25 \sin θ - (13 μ_{A} + 12 μ_{B}) \cos θ) t_{1}^{2} + g (5 \sin θ - (2 μ_{A} + 3 μ_{B}) \cos θ) t_{1} (2 t_{1}) + \frac{1}{2} g (\sin θ - μ_{A} \cos θ) {(2 t_{1})}^{2} \\ x_{4} = \frac{1}{2} g (49 \sin θ - (25 μ_{A} + 24 μ_{B}) \cos θ) t_{1}^{2} \end{array}$

Las velocidades de los dos cuerpos, en el instante 7t₁, antes del choque, son

$\begin{array}{l} {\begin{cases} u_{A} = v_{0 A} + a_{A} t_{4} \\ u_{B} = v_{0 B} + a_{B} t_{4} \end{cases} \\ {\begin{cases} u_{A} = g (5 \sin θ - (2 μ_{A} + 3 μ_{B}) \cos θ) t_{1} + g (\sin θ - μ_{A} \cos θ) (2 t_{1}) = g (7 \sin θ - (4 μ_{A} + 3 μ_{B}) \cos θ) t_{1} \\ u_{B} = g (5 \sin θ - (2 μ_{B} + 3 μ_{A}) \cos θ) t_{1} + g (\sin θ - μ_{B} \cos θ) (2 t_{1}) = g (7 \sin θ - (3 μ_{A} + 4 μ_{B}) \cos θ) t_{1} \end{cases} \end{array}$

Cuarta etapa

Así, sucesivamente ...

Cálculo y representación gráfica

Consideremos el siguiente sistema

Angulo del plano inclinado, θ=π/6 (30°)
Coeficiente cinético de rozamiento entre el cuerpo A y el plano inclinado, μ_A=0.2
Coeficiente cinético de rozamiento entre el cuerpo B y el plano inclinado, μ_B=0.4
Distancia inicial entre los dos cuerpos, d=1 m

Se cumple que tan θ>μ_B>μ_A.

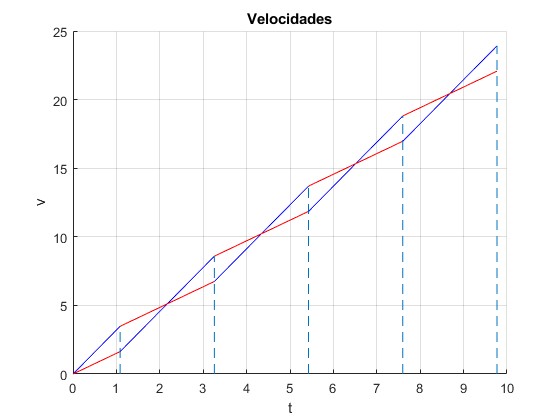
Representamos las velocidades de los dos cuerpos en función del tiempo. (del cuerpo A en color azul y del B en color rojo). La línea a trazos marca los instantes en los que se produce el choque, t₁, 3t₁, 5t₁, 7t₁,...

th=pi/6; %ángulo del plano inclinado
mu_B=0.4; %coef. rozamiento B-plano
mu_A=0.2; %coef. rozamiento A-plano
d=1; %separación inicial
t1=sqrt(2*d/((mu_B-mu_A)*9.8*cos(th)));
a_A=9.8*(sin(th)-mu_A*cos(th));
a_B=9.8*(sin(th)-mu_B*cos(th));
x1=a_A*t1^2/2;
u_A=a_A*t1;
u_B=a_B*t1;
line([0,t1],[0,u_A],'color','b')
line([0,t1],[0,u_B],'color','r')
line([t1,t1],[0, u_A],'lineStyle','--')
for i=1:4
    v0_A=u_B;
    v0_B=u_A;
    u_A=v0_A+a_A*(2*t1);
    u_B=v0_B+a_B*(2*t1);
    line([t1+(i-1)*(2*t1),t1+i*(2*t1)],[v0_A,u_A],'color','b')
    line([t1+(i-1)*(2*t1),t1+i*(2*t1)],[v0_B,u_B],'color','r')
    line([t1+i*(2*t1),t1+i*(2*t1)],[0, u_A],'lineStyle','--')
end
grid on
xlabel('t')
ylabel('v')
title('Velocidades')

Representamos las posiciones de los dos cuerpos en función del tiempo. (del cuerpo A en color azul y del B en color rojo). La posición inicial de A es x_A=0 y de B x_B=d

th=pi/6; %ángulo del plano inclinado
mu_B=0.4; %coef. rozamiento B-plano
mu_A=0.2; %coef. rozamiento A-plano
d=1; %separación inicial
t1=sqrt(2*d/((mu_B-mu_A)*9.8*cos(th)));
a_A=9.8*(sin(th)-mu_A*cos(th));
a_B=9.8*(sin(th)-mu_B*cos(th));
%etapa incial
x0=a_A*t1^2/2;
u_A=a_A*t1;
u_B=a_B*t1;
hold on
x_A=@(t) a_A*t.^2/2;
x_B=@(t) d+a_B*t.^2/2;
fplot(x_A,[0,t1], 'color','b')
fplot(x_B,[0,t1], 'color','r')
plot(t1,x_A(t1),'ko','markersize',3,'markerfacecolor','k')
line([t1,t1],[0, x_A(t1)],'lineStyle','--')
for i=1:3
    v0_A=u_B;
    v0_B=u_A;
    xf=x0+v0_A*(2*t1)+a_A*(2*t1)^2/2;
    u_A=v0_A+a_A*(2*t1);
    u_B=v0_B+a_B*(2*t1);
    x_A=@(t) x0+v0_A*(t-t1-(i-1)*(2*t1))+a_A*(t-t1-(i-1)*(2*t1)).^2/2;
    x_B=@(t)  x0+v0_B*(t-t1-(i-1)*(2*t1))+a_B*(t-t1-(i-1)*(2*t1)).^2/2;
    fplot(x_A ,[t1+(i-1)*(2*t1),t1+i*(2*t1)], 'color','b')
    fplot(x_B,[t1+(i-1)*(2*t1),t1+i*(2*t1)], 'color','r')
    plot(t1+i*(2*t1),x_A(t1+i*(2*t1)),'ko','markersize',3,
'markerfacecolor','k')
    line([t1+i*(2*t1),t1+i*(2*t1)],[0, x_A(t1+i*(2*t1))],'lineStyle','--')
    x0=xf;
end
hold off
grid on
xlabel('t')
ylabel('x')
title('Desplazamientos')

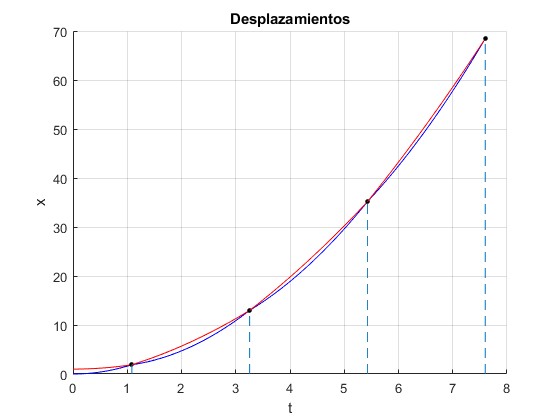
Los puntos de color negro, señalan las posciones en las que ocurren los choques

Comprobación, posición de encuentro x₄

>xf =   68.4508
>> 4.9*(49*sin(th)-(25*mu_A+24*mu_B)*cos(th))*t1^2
ans =   68.4508

Referencias

Indian National Physics Olympiad. Homi Bhabha Centre for Science Eduaction. Solved papers NSEP & INPhO, 2016-2018, Ejemplo 3, enunciado, 213, solución, 216-218