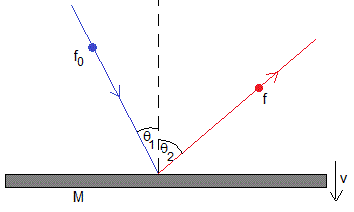
Consideremos un fotón de energía hf₀ y de momento lineal hf₀/c, que choca oblicuamente con una superficie perfectamente reflectante de masa M que se mueve con velocidad v. Supondremos que esta velocidad es pequeña comparada con la velocidad c de la luz, v<<c.

Como consecuencia del choque elástico entre el fotón y la superficie reflectante, el ángulo de incidencia θ₁ no será igual al de reflexión, θ₂, ni la frecuencia del fotón f₀ incidente será igual al la frecuencia f del fotón reflejado por dicha superficie.

Principios de conservación

• Principio de conservación del momento lineal (sistema aislado)

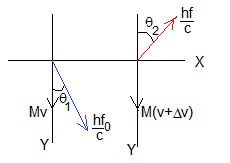
Dibujamos los vectores momento lineal del fotón y del espejo antes (izquierda) y después (derecha) del choque.

• Conservación del momento lineal a lo largo del eje X

${\displaystyle \frac{h{f}_0}{c}\sin {\theta }_1=\frac{hf}{c}\sin {\theta }_2}$

• Conservación del momento lineal a lo largo del eje Y

${\displaystyle Mv+\frac{h{f}_0}{c}\cos {\theta }_1=-\frac{hf}{c}\cos {\theta }_2+M(v+\Delta v)}$

Donde Δv, es el cambio de velocidad del espejo en la dirección del eje Y.

• Conservación de la energía (choque elástico)

${\displaystyle h{f}_0+\frac{1}{2}M{v}^2=hf+\frac{1}{2}M{\left(v+\Delta v\right)}^2}$

La ecuación de conservación del momento lineal a lo largo del eje Y y la ecuación de conservación de la energía se escriben

${\displaystyle \begin{array}{l}M\Delta v=\frac{h}{c}\left(f_0\cos {\theta }_1+f\cos {\theta }_2\right)\\ h{f}_0=hf+v·\left(M\Delta v\right)+\frac{1}{2M}{\left(M\Delta v\right)}^2\end{array}}$

Se transforman en la ecuación

${\displaystyle h{f}_0=hf+\frac{hv}{c}\left(f_0\cos {\theta }_1+f\cos {\theta }_2\right)+\frac{h^2}{2M{c}^2}{\left(f_0\cos {\theta }_1+f\cos {\theta }_2\right)}^2}$

El tercer término se puede despreciar, ya que en el numerador aparece el cuadrado de la constante h de Planck, en el denominador aparece la masa del espejo, M multiplicada por el cuadrado de la velocidad de la luz, c

${\displaystyle \begin{array}{l}{f}_0\approx f+\frac{f_{0}v}{c}\left(f_0\cos {\theta }_1+f\cos {\theta }_2\right)\\ f=f_0\frac{1-\frac{v}{c}\cos {\theta }_1}{1+\frac{v}{c}\cos {\theta }_2}\end{array}}$

Relación entre le ángulo de incidencia y el reflejado

La ecuación de conservación del momento lineal a lo largo del eje X se escribe, f₀sinθ₁=fsinθ₂. Conocida la relación entre las frecuencias f₀ y f

${\displaystyle \left(1+\frac{v}{c}\cos {\theta }_2\right)\sin {\theta }_1=\left(1-\frac{v}{c}\cos {\theta }_1\right)\sin {\theta }_2}$

Despejamos cosθ₂, siguiendo el mismo procedimiento que al final de la página titulada 'Principio de Fermat'

Elevamos al cuadrado para sustituir sin²θ₂=1-cos²θ₂, obteniendo una ecuación de segundo grado en cosθ₂

${\displaystyle \begin{array}{l}{\left(1-\frac{v}{c}\cos {\theta }_1\right)}^2\left(1-{\cos }^2{\theta }_2\right)={\left(1+\frac{v}{c}\cos {\theta }_2\right)}^2\left(1-{\cos }^2{\theta }_1\right)\\ \left(1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1\right){\cos }^2{\theta }_2+\left(2\frac{v}{c}(1-{\cos }^2{\theta }_1)\right)\cos {\theta }_2+2\frac{v}{c}\cos {\theta }_1-\left(1+\frac{v^2}{c^2}\right){\cos }^2{\theta }_1=0\\ \cos {\theta }_2=\frac{-\frac{v}{c}\left(1-{\cos }^2{\theta }_1\right)\pm \sqrt{\frac{v^2}{c^2}{\left(1-{\cos }^2{\theta }_1\right)}^2-\left(1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1\right)\left(2\frac{v}{c}-\left(1+\frac{v^2}{c^2}\right)\cos {\theta }_1\right)\cos {\theta }_1}}{\left(1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1\right)}\end{array}}$

Utilizamos Math Symbolic de MATLAB para simplificar y factorizar el discriminante. Llamamos k a v/c y x a cosθ₁

>> syms k x;
>> y=k^2*(1-x^2)^2-(1+k^2-2*k*x)*(2*k*x-(1+k^2)*x^2);
>> factor(y)
 ans =[ k - x, k - x, k*x - 1, k*x - 1]

Las dos raíces de la ecuación de segundo grado son

${\displaystyle \begin{array}{l}\cos {\theta }_2=\frac{-\frac{v}{c}\left(1-{\cos }^2{\theta }_1\right)\pm \left(\frac{v}{c}-\cos {\theta }_1\right)\left(\frac{v}{c}\cos {\theta }_1-1\right)}{\left(1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1\right)}\\ {\left(\cos {\theta }_2\right)}_1=\frac{-2\frac{v}{c}+\left(1+\frac{v^2}{c^2}\right)\cos {\theta }_1}{\left(1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1\right)}\\ {\left(\cos {\theta }_2\right)}_2=\frac{2\frac{v}{c}{\cos }^2{\theta }_1-\left(1+\frac{v^2}{c^2}\right)\cos {\theta }_1}{\left(1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1\right)}\end{array}}$

De las dos soluciones solamente una es correcta, probamos cuando el espejo está inmóvil v=0, el ángulo de incidencia tiene que ser igual al de reflexión, θ₁=θ₂

• La primera solución, cosθ₂=cosθ₁
• La segunda solución, cosθ₂=-cosθ₁ que no es correcta

La relación entre el ángulo de incidencia θ₁ y de reflexión θ₂, es

${\displaystyle \cos {\theta }_2=\frac{\left(1+\frac{v^2}{c^2}\right)\cos {\theta }_1-2\frac{v}{c}}{\left(1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1\right)}}$

Relación entre frecuencias

Sustituyendo cosθ₂ en la relación de frecuencias

${\displaystyle \begin{array}{l}f=f_0\frac{1-\frac{v}{c}\cos {\theta }_1}{1+\frac{v}{c}\cos {\theta }_2}\\ f=f_0\frac{\left(1-\frac{v}{c}\cos {\theta }_1\right)\left(1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1\right)}{\left(1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1\right)+\frac{v}{c}\left(\left(1+\frac{v^2}{c^2}\right)\cos {\theta }_1-2\frac{v}{c}\right)}\\ f=f_0\frac{\left(1-\frac{v}{c}\cos {\theta }_1\right)\left(1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1\right)}{1-\frac{v^2}{c^2}-\frac{v}{c}\cos {\theta }_1+\frac{v^3}{c^3}\cos {\theta }_1}\end{array}}$

Simplificamos

${\displaystyle f=f_0\frac{1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1}{1-\frac{v^2}{c^2}}}$

Obteniendo el mismo resultado que en la página titulada 'Efecto Doppler en las ondas electromagnéticas'

Referencias

Aleksandar Gjurchinovski. Reflection from a moving mirror-a simple derivation using the photon model of light. Eur. J. Phys. 34 (2013) pp. L1-L4