El escalón de potencial
El escalón de potencial (E>V0)
En el capítulo Movimiento Ondulatorio vimos que una onda luminosa o mecánica al atravesar la superficie de separación de dos medios de distintas propiedades ópticas o mecánicas, una parte se refleja y otra se transmite. La proporción de la intensidad de la onda incidente que se transmite se denomina coeficiente de transmisión, y la proporción de la intensidad de la onda incidente que se refleja se denomina coeficiente de reflexión.
La ecuación de Schrödinger independiente del tiempo en una región unidimensional cuya energía potencial viene descrita por la función Ep(x) es
Donde E es la energía total de la partícula de masa m
La solución de la ecuación de Schrödinger Ψ(x) se denomina función de onda.
La probabilidad de encontrar la partícula descrita por dicha función de onda en el intervalo x, x+dx es |Ψ(x)|2·dx. Naturalmente,
En otras palabras, la probabilidad por unidad de longitud (o densidad de probabilidad) de encontrar la partícula en x es |Ψ(x)|2 .
Si tenemos N partículas idénticas, N·|Ψ(x)|2 , nos dará el número de partículas que hay en la unidad de longitud. Si todas las partículas se mueven con la misma velocidad v, el flujo de partículas será N·v|Ψ(x)|2 . Se denomina densidad de corriente de probabilidad a la cantidad J=v|Ψ(x)|2 que es el producto de la velocidad de las partículas por la densidad de probabilidad.
Partícula libre
El caso más simple es el de una partícula libre. La energía potencial Ep(x)=0
La ecuación de Schrödinger se escribe
Ecuación diferencial análoga a la de un movimiento armónico simple, su solución la expresaremos
Escalón de potencial
El escalón de potencial consiste en una región x<0 en la que la energía potencial es nula, seguida de una región x>0 en la que la energía potencial es constante y de valor V0.
La función Ep(x) presenta por tanto, una discontinuidad en x=0.
Se pueden presentar dos casos
- Que la energía de la partícula sea mayor que la del escalón E>V0.
- Que la energía de la partícula sea menor que la del escalón E<V0.
En este apartado trataremos el primer caso, dejando el segundo caso, algo más complejo, para el siguiente.
Planteamos la ecuación de Schrödinger en cada una de las regiones y hallamos su solución de forma semejante al de la partícula libre. En la siguiente tabla se resumen los resultados.
| Región x<0, Ep(x)=0 | Región x>0, Ep(x)=V0 |
|---|---|
En el punto x=0, la función de onda Ψ debe ser continua y también lo debe ser su derivada primera.
Lo que da lugar a un sistema de dos ecuaciones con dos incógnitas que nos permiten expresar los coeficientes B y C en función del coeficiente A.
Veamos ahora el significado físico de los distintos términos de la solución de la ecuación de Schrödinger. En la primera región x<0 tenemos partículas incidentes y reflejadas, pero en la segunda región x>0 solamente tenemos partículas transmitidas. La función de onda tiene dos términos en la primera región y un solo término en la segunda.
| Partículas | Función de onda | Probabilidad | Flujo |
|---|---|---|---|
| incidentes | |||
| reflejadas | |||
| transmitidas |
Se denomina coeficiente de reflexión a la proporción de partículas incidentes que se reflejan
Se denomina coeficiente de transmisión a la proporción de partículas incidentes que se transmiten.
Como puede fácilmente comprobarse R+T=1
Recordaremos que en un movimiento ondulatorio, una onda incidente al atravesar dos medios de distinta naturaleza (densidad, índice de refracción, etc., dependiendo del tipo de onda) da origen a una onda reflejada que se propaga en el primer medio y a una onda transmitida, que se propaga en el segundo medio.
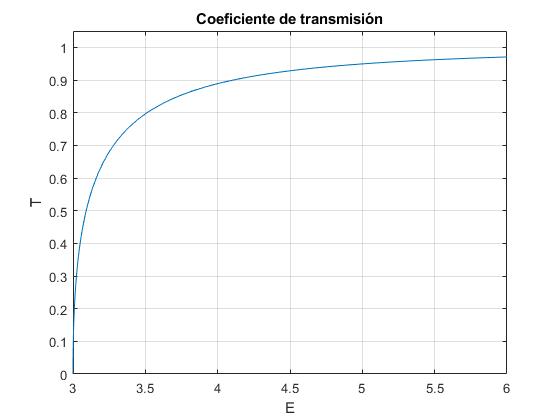
Representamos el coeficiente de transmisión T en función de la energía (E>V0) para V0=3
V0=3; %altura escalón
f=@(E) 4*sqrt(E).*sqrt(E-V0)./(sqrt(E)+sqrt(E-V0)).^2;
fplot(f,[V0,2*V0])
grid on
ylim([0,1.05])
xlabel('E')
ylabel('T')
title('Coeficiente de transmisión')
Cuando la energía E>>V0 el coeficiente T→1
Actividades
Se introduce la energía de la partícula mayor que uno en el control titulado Energía
Se pulsa en el botón Nuevo, para que las partículas incidentes se reflejen o se transmitan. En la parte izquierda se contabilizan el número de partículas incidentes y el número de partículas reflejadas.
Se desactiva la casilla titulada Ver movimiento, si no estamos interesados en ver el movimiento de la partícula, sino tan sólo en la proporción de partículas incidentes que se reflejan, para cada valor de la energía E que introducimos.
Observar que no podemos predecir la conducta de una partícula individual, si se va a reflejar o se va a transmitir.
Completar la siguiente tabla, calculando el cociente entre el número de partículas reflejadas y el número de partículas incidentes en la cuarta columna.
Compararlo con el coeficiente de reflexión deducido a partir de la ecuación de Schrödinger
| Energía | Partículas incidentes | Partículas reflejadas | Cociente reflej./incidentes | Coef. reflexión (teórico) |
|---|---|---|---|---|
1.1 |
||||
1.2 |
||||
1.3 |
||||
1.4 |
||||
El escalón de potencial (E<V0)
Desde el punto de vista clásico, la partícula tiene una energía cinética igual a la energía total E, a la izquierda del origen, ya que la energía potencial es cero. Sin embargo, tiene una energía cinética negativa a la derecha del origen ya que la energía potencial es mayor que la energía total. De acuerdo con la interpretación de la Mecánica Clásica, la partícula no podrá moverse en la región x>0, la partícula rebotará en el origen x=0.
La solución de la ecuación de Schrödinger en ambas regiones, indica que toda partícula incidente se refleja, pero existe una probabilidad no nula de encontrar partículas a la derecha de origen, en la región clásicamente prohibida, y esta probabilidad disminuye rápidamente a medida que nos adentramos en la citada región. En concreto, la probabilidad disminuye exponencialmente con la distancia x al origen.
El fenómeno análogo ondulatorio es la reflexión total, más allá de la superficie de separación entre los dos medios se puede detectar movimiento ondulatorio. La onda transmitida se amortigua exponencialmente en la dirección perpendicular a la superficie de separación. Sin embargo, el flujo medio de energía en la dirección normal es nulo, lo que quiere decir que toda la intensidad de la onda incidente se refleja.
Planteamos la ecuación de Schrödinger en cada una de las regiones y hallamos su solución.
Comparando con la obtenida para el escalón de potencial con E>V0, nos daremos cuenta que al ser E<V0, q2 es negativo y por tanto, q es imaginario, llamaremos α=iq.
La solución de la ecuación de Schrödinger para ambas regiones x<0 y x>0 se escribirá.
| Región x<0, Ep(x)=0 | Región x>0, Ep(x)=V0 |
|---|---|
En el punto x=0, la función de onda Ψ debe ser continua y también lo debe ser su derivada primera.
Lo que da lugar a un sistema de dos ecuaciones con dos incógnitas que nos permiten expresar los coeficientes B y C en función del coeficiente A.
Veamos ahora el significado físico de los distintos términos de la solución de la ecuación de Schrödinger. En la primera región x<0, tenemos partículas incidentes y reflejadas, pero en la segunda región x>0 solamente tenemos la exponencial negativa, ya que la positiva tiende a infinito cuando cuando x se hace grande. La función de onda tiene por tanto, dos términos en la primera región y un solo término en la segunda.
| Partículas | Función de onda | Probabilidad |
|---|---|---|
| incidentes | ||
| reflejadas | ||
| transmitidas |
El hecho de que Ψt(x) sea distinto de cero significa que hay alguna probabilidad de encontrar la partícula a la derecha del origen. Dicha probabilidad disminuye rápidamente cuando x crece. En general, la partícula no podrá penetrar mucho dentro de la región clásicamente prohibida.
Como podemos comprobar |A|2=|B|2, por tanto, todas las partículas que alcanzan el escalón de potencial rebotan, incluyendo aquellas que penetran en la región a la derecha del origen.
Actividades
El programa interactivo nos permite ensayar con dos tipos de partículas los electrones y los protones, la masa de ambas partículas está en la relación 1/1836, y con otras partículas hipotéticas cuya masa está comprendida entre estos dos valores extremos. Observaremos que la penetración en la región clásicamente prohibida depende fuertemente de la masa de la partícula, siendo mayor cuanto menor sea ésta.
Para comprobarlo, situaremos a lo largo del eje X, detectores que van a registrar las partículas que penetran hasta una distancia x, en el interior del escalón de potencial. Un diagrama de barras nos mostrará el número de partículas registradas en cada detector.
Se introduce
- el valor de la energía (menor que uno), en el control titulado Energía.
- la masa de la partícula, en el control titulado Masa o bien, se selecciona el tipo de partícula, Protón o Electrón, actuando sobre el botón de radio correspondiente
Se pulsa en el botón Nuevo, para que las partículas incidentes penetren en la barrera de potencial y se reflejen. En la parte izquierda, se contabilizan el número de partículas incidentes y el número de partículas reflejadas.
Se activa la casilla titulada Ver movimiento para visualizar el movimiento de la partícula incidente y reflejada. En el caso de que la casilla esté sin activar solamente se muestra el destello de la partícula cuando es registrada por un detector situado a una distancia x del origen.
Comprobar que toda partícula incidente se refleja, como se muestra en los contadores situados en la parte superior izquierda.
Observar que no podemos predecir la conducta de una partícula individual, hasta que distancia x penetrará en la región a la derecha del origen. Sin embargo, podemos decir que tiene más probabilidad de ser detectada cerca del origen.
Observar que cuando el número de partículas incidentes es grande, el diagrama de barras se va ajustando a una curva exponencial decreciente.
Comprobar que es muy pequeña la probabilidad de detectar protones en el interior del escalón de potencial, debido a que su masa es muy grande, del orden 1836 veces mayor que la de un electrón.
Observar y describir los diagramas de barras producidos para cada energía por los electrones y los protones, y por otras partículas hipotéticas cuya masa esté comprendida entre la de un electrón y la de un protón.

