El efecto fotoeléctrico
La emisión de electrones por metales iluminados con luz de determinada frecuencia fue observada a finales del siglo XIX por Hertz y Hallwachs. El proceso por el cual se liberan electrones de un material por la acción de la radiación se denomina efecto fotoeléctrico o emisión fotoeléctrica. Sus características esenciales son:
- Para cada sustancia hay una frecuencia mínima o umbral de la radiación electromagnética por debajo de la cual no se producen fotoelectrones por más intensa que sea la radiación.
- La emisión electrónica aumenta cuando se incrementa la intensidad de la radiación que incide sobre la superficie del metal, ya que hay más energía disponible para liberar electrones.
En los metales hay electrones que se mueven más o menos libremente a través de la red cristalina, estos electrones no escapan del metal a temperaturas normales por que no tienen energía suficiente. Calentando el metal es una manera de aumentar su energía. Los electrones "evaporados" se denominan termoelectrones, este es el tipo de emisión que hay en las válvulas electrónicas. Vamos a ver que también se pueden liberar electrones (fotoelectrones) mediante la absorción por el metal de la energía de radiación electromagnética.
Denominamos φ la energía mínima necesaria para que un electrón escape del metal. Si el electrón absorbe una energía E, la diferencia E-φ, será la energía cinética del electrón emitido.
Ek=E-φ
La teoría de la fotoemisión explica el significado correcto de φ, es preciso conocer la estructura de las bandas de valencia de los metales cátodo (emisor) y del ánodo (receptor) cuando se conectan y se establece una diferencia de potencial entre los mismos
Einstein explicó las características del efecto fotoeléctrico, suponiendo que cada electrón absorbía un cuanto de radiación o fotón. La energía de un fotón se obtiene multiplicando la constante h de Planck por la frecuencia f de la radiación electromagnética.
E=hf
Si la energía del fotón E, es menor que la energía de arranque φ, no hay emisión fotoeléctrica. En caso contrario, si hay emisión y el electrón sale del metal con una energía cinética Ek igual a E-φ.
Por otra parte, cuando la placa de área S se ilumina con cierta intensidad I, absorbe una energía en la unidad de tiempo proporcional a IS, basta dividir dicha energía entre la cantidad hf para obtener el número de fotones que inciden sobre la placa en la unidad de tiempo. Como cada electrón emitido toma la energía de un único fotón, concluimos que el número de electrones emitidos en la unidad de tiempo es proporcional a la intensidad de la luz que ilumina la placa
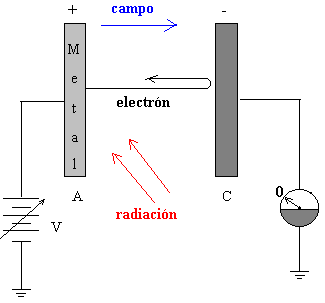
Mediante una fuente de potencial variable, tal como se ve en la figura medimos la energía cinética máxima de los electrones emitidos.
Aplicando una diferencia de potencial V entre las placas A y C se frena el movimiento de los fotoelectrones emitidos. Para un voltaje V0 determinado, el amperímetro no marca el paso de corriente, lo que significa que ni aún los electrones más rápidos llegan a la placa C. En ese momento, la energía potencial de los electrones se hace igual a la energía cinética.
eV0=hf-φ
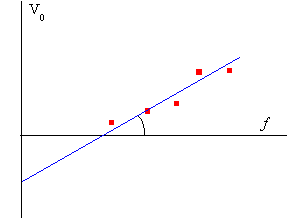
Variando la frecuencia f, (o la longitud de onda de la radiación que ilumina la placa) obtenemos un conjunto de valores del potencial de detención V0. Llevados a un gráfico obtenemos una serie de puntos (potencial de detención, frecuencia) que se aproximan a una línea recta.
La ordenada en el origen mide la energía de arranque en electrón-voltios φ/e. Y la pendiente de la recta es h/e. Utilizando el valor de la carga del electrón e= 1.6 10-19 C, obtendremos el valor de la constante de Planck, h=6.63 10-34 Js.
No es posible disponer de lámparas que emitan a todas las frecuencias posibles, solamente existen lámparas hechas de materiales cuya emisión corresponde a unas determinadas líneas del espectro. Algunas de las líneas de emisión son muy débiles y otras son brillantes.
En las tablas que vienen a continuación se proporcionan los espectros de emisión de metales y gases. La longitud de onda se da en angstrom (10-10 m). Los números en negrita indican las líneas de mayor brillo. La mayor parte de las líneas se encuentran dentro del espectro visible.
| Aluminio (arco) | Cobre (arco en el vacío) | Mercurio (lámpara de arco) | Sodio (en llama) | Cadmio (arco) | Cinc (arco en el vacío) |
|---|---|---|---|---|---|
| 3083
3093 3944 3962 4663 5057 5696 5723 |
3248
3274 4023 4063 5105 5153 5218 5700 5782 |
3126
3131 3650 4047 4358 4916 4960 5461 5770 5791 6152 6232 |
5890
5896 |
3261
3404 3466 3611 3982 4413 4678 4800 5086 5338 5379 6438 |
3036
3072 3345 4680 4722 4811 4912 4925 6103 6332 |
| Argón | Helio | Hidrógeno | Neón | Nitrógeno |
|---|---|---|---|---|
| 3949
4044 4159 4164 4182 4190 4191 4198 4201 4251 4259 4266 4272 4300 4334 4335 |
3889
4026 4221 5016 5876 6678 7065 |
4102
4340 4341 4861 6563 |
4538
4576 4704 4709 4715 4789 5331 5341 5358 5401 5853 5882 5965 6143 6266 6383 6402 6506 7174 7245 |
5754
5803 5853 5904 5957 6012 6068 6251 6321 6393 6467 6543 6622 6703 6787 |
Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física Elemental. Editorial Mir 1975., págs. 213-214
Actividades
Para realizar la práctica que simula el efecto fotoeléctrico se han de seguir los siguientes pasos:
- Se elige el material de la placa metálica con el que experimentar el efecto fotoeléctrico, en el control titulado Cátodo.
Se pulsa en el botón titulado Nuevo
Se selecciona el espectro de emisión del metal o gas en el control de selección titulado Espectro de emisión. La longitud de onda se puede cambiar actuando en la barra de desplazamiento o introduciendo otro valor en el control de edición. Si no hay emisión, elegir una línea de emisión de menor longitud de onda (mayor frecuencia).
La frecuencia f=c/λ=2997.9/λ, la longitud de onda λ se expresa en unidades de 10-9 m y la frecuencia f en 1014 Hz. c=2.9979·108 m/s es la velocidad de la luz en el vacío.Se introduce la intensidad de la radiación un número mayor que cero, en el control titulado Intensidad luz. Comprobamos que cuando mayor sea la intensidad mayor es el número de fotones, mayor es el número de electrones emitidos y mayor es la intensidad de la corriente lo que se muestra en la desviación del de la aguja del amperímetro.
Se modifica el potencial variable de la batería, introduciendo otro valor en el control titulado d.d.p.(V), hasta conseguir que el electrón llegue justo a la placa opuesta, el amperímetro deja de marcar el paso de corriente, o empieza a marcar el paso de corriente.
Se pulsa en el botón titulado ►
Se realiza la experiencia
| Metal: Cesio | |
| Longitud de onda | Potencial V0 |
|---|---|
| 510 | 0.55 |
| 515 | 0.53 |
| 521 | 0.50 |
| 570 | 0.29 |
| 578 | 0.26 |
>> f=(2.9979*10^3)./[510,515,521,570,578];
>> V=[0.55,0.53,0.50,0.29,0.26];
>> plot(f,V,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
>> grid on
>> xlabel('f*10^{14} Hz')
>> ylabel('V')
>> title('Efecto fotoeléctrico')
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.
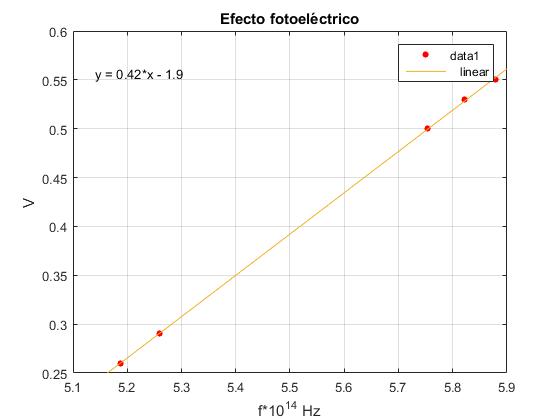
Se obtiene la energía de arranque de los electrones del metal leyendo la ordenada en el origen de la recta trazada, parámetro p2=1.9328 eV
La pendiente de la recta es el valor del parámetro p1=0.42273 y mide el cociente entre las constantes fundamentales h/e
Para obtener el valor de la constante h de Planck, se debe tener en cuenta que el eje horizontal es la frecuencia de la radiación electromagnética en unidades 1014 Hz. La carga del electrón es 1.6·10-19 C. Por tanto, el valor de h se obtiene multiplicando la pendiente p1 por la carga e y dividiendo por el factor 1014.
h=p1·1.6 10-19/1014=p1·1.6 10-33 Js
>> 0.42273*1.6e-33 ans = 6.7637e-34
Energía de arranque: φ=1.9 V
Constante de Planck: h=6.76·10-34 J·s

