La capacidad de uno de los condensadores es constante

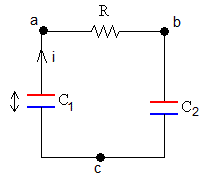
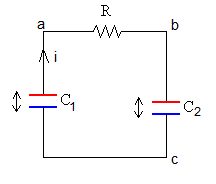
Consideremos el siguiente dispositivo formado por dos condensadores plano-paralelos C₁ y C₂ y una resistencia R, tal como se muestra en la figura. Los dos condensadores tienen la misma área S de las placas y la misma separación d. La capacidad inicial de los condensadores es C₁=C₂=εS/d

Cada uno de los condensadores se conecta a una batería de fem V₀, adquiriendo la misma carga inicial q₀₁=V₀·C₁, q₀₂=V₀·C₂. La carga total cuando se conectan en paralelo es Q=q₀₁+q₀₂=2V₀(εS/d)

Una de las placas del primer condensador es móvil de modo que la separación entre las mismas varía con el tiempo de la forma d₁=d+Asin(ωt). Su capacidad C₁ cambia con el tiempo de la forma

${\displaystyle C_1=\frac{\epsilon S}{d+A\sin (\omega t)}}$

Las placas del segundo condensador son fijas y la separación entre las mismas es d₂=d. Su capacidad C₂ es constante

${\displaystyle C_2=\frac{\epsilon S}{d}}$

Ecuación del circuito

En un instante t las cargas de los condensadores son q₁ y q₂, respectivamente. La diferencia de potencial entre las placas de cada uno de los condensadores es (la placa positiva tiene mayor potencial que la negativa)

${\displaystyle V_{ac}=\frac{q_1}{C_1}{V}_{bc}=\frac{q_2}{C_2}}$

Supongamos que por la resistencia R circula una corriente de intensidad i, en el sentido indicado mediante una flecha en la figura.

La ecuación del circuito es

${\displaystyle \begin{array}{l}{V}_{ab}+V_{bc}+V_{ca}=0\\ iR+\frac{q_2}{C_2}-\frac{q_1}{C_1}=0\end{array}}$

La carga total q₁+q₂ permanece constante e igual a la inicial Q=q₀₁+q₀₂. La intensidad es i=-dq₁/dt=dq₂/dt. (Si la intensidad tiene el sentido indicado en la figura, la carga q₁ disminuye con el tiempo t). Expresamos la ecuación del circuito en términos de las variables q₁ y t

${\displaystyle \begin{array}{l}-R\frac{d{q}_1}{dt}+\left(Q-q_1\right)\frac{d}{\epsilon S}-q_1\frac{d+A\sin (\omega t)}{\epsilon S}=0\\ \frac{d{q}_1}{dt}=\frac{1}{\epsilon SR}\left(-q_1\left(d+A\sin (\omega t)\right)+(Q-q_1)d\right)\end{array}}$

Resolvemos la ecuación diferencial por procedimientos numéricos con las siguiente condición inicial, en el instante t=0, la carga del primer condensador es q₀₁.

Datos:

• Separación entre las placas del condensador, d=2
• Area de las placas del condensador, S=10
• Permitividad de la sustancia dieléctrica, ε=10
• Resistencia del circuito, R=0.1
• La separación d₁ entre las placas del primer condensador, varía con el tiempo con una amplitud A=1 y un periodo P=20

${\displaystyle d_1=d+A\sin \left(\frac{2\pi }{P}t\right)}$

• Inicialmente, t=0, los dos condensadores se cargan conectándolos a una batería de V₀=100 V. La carga inicial que adquieren cada uno de los dos condensadores, q₀₁=q₀₂ es

${\displaystyle q_{01}=V_0\frac{\epsilon S}{d}}$

A=1;  %amplitud
w=2*pi/20; %frecuencia angular
d=2;    %separación inicial
S=10; % area de las placas
epsilon=10; %permitividad
R=0.1; %resistencia
eS=epsilon*S;
V0=100; %fem de la batería que carga inicialmente los condensadores
Q=2*V0*eS/d;  %carga total

tspan=[0 150]; 
f=@(t,x) (-x*(d+A*sin(w*t))+(Q-x)*d)/(eS*R);
[t,q1]=ode45(f,tspan,Q/2);

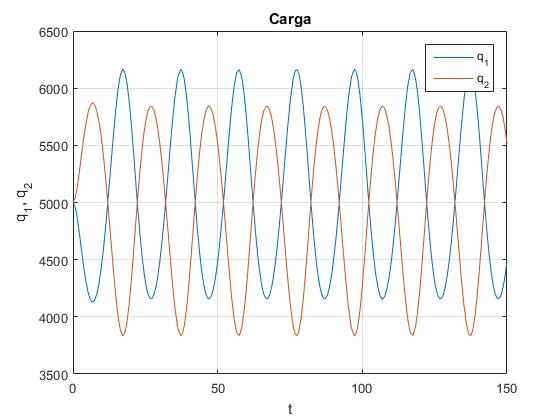
plot(t,q1, t, Q-q1)
grid on
legend('q_1','q_2')
xlabel('t')
ylabel('q_1, q_2');
title('Carga')

figure
V1=q1.*(d+A*sin(w*t))/eS;
V2=(Q-q1)*d/eS;
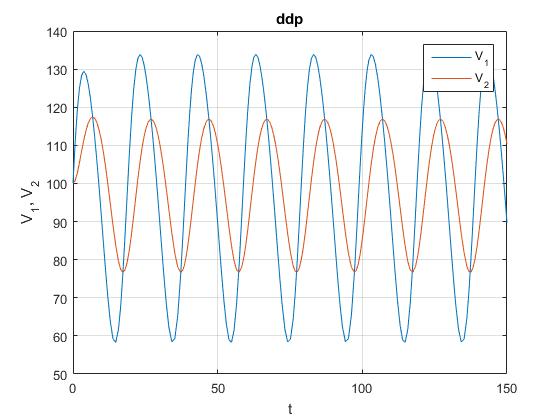
plot(t,V1,t,V2)
grid on
legend('V_1','V_2')
xlabel('t')
ylabel('V_1, V_2');
title('ddp')

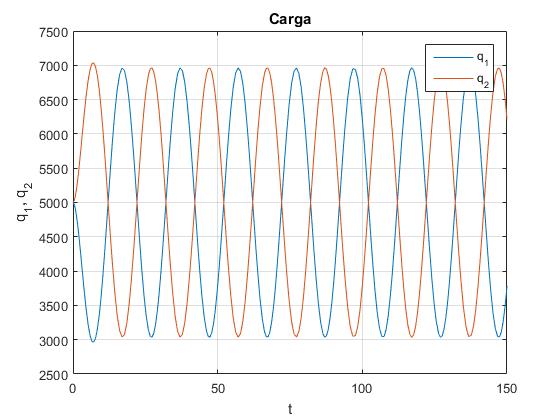
Carga de cada uno de los condensadores q₁ y q₂ en función del tiempo t

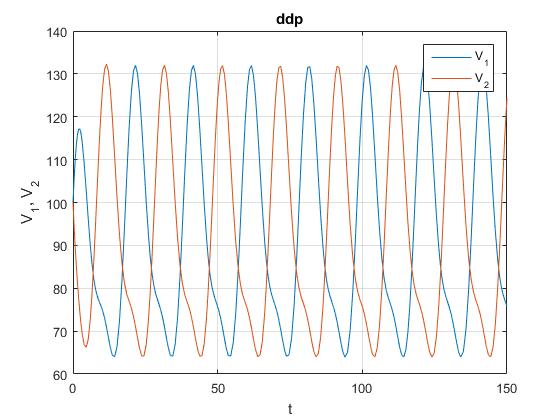
Diferencia de potencial entre las placas de cada uno de los condensadores V₁ y V₂ en función del tiempo t

Trabajo y energía

Vamos a realizar el balance energético del sistema, calculando

• La energía electrostática acumulada por los condensadores
• La energía disipada en la resistencia
• El trabajo mecánico necesario para mover las placas del primer condensador

La energía acumulada por un condensador de capacidad C cargado con una carga q es

${\displaystyle U=\frac{1}{2}\frac{q^2}{C}}$

En el instante t=0, los condensadores cuyas capacidades son C₁=C₂=εS/d, han sido cargados poniéndolos en contacto con una batería de fem V₀, adquiriendo cargas q₀₁=q₀₂=V₀·(εS/d)

En el instante t, las cargas de los condensadores son q₁ y q₂=Q-q₁, sus capacidades son C₁=εS/(d+Asin(ωt)) y C₂=εS/d

La variación de energía eléctrostática ΔU=ΔU₁+ΔU₂ acumulada en los condensadores es

${\displaystyle \begin{array}{l}\Delta U_1=\frac{1}{2}\frac{q_1^2}{C_1}-\frac{1}{2}\left(\frac{\epsilon S}{d}\right)V_0^2\\ \Delta U_2=\frac{1}{2}\frac{q_2^2}{C_2}-\frac{1}{2}\left(\frac{\epsilon S}{d}\right)V_0^2\end{array}}$

Calculamos la variación de energía ΔU entre los instantes t=0 y t=150

>> DU=q1(end)^2*(d+A*sin(w*t(end)))/(2*eS)+
(Q-q1(end))^2*d/(2*eS)-V0^2*eS/d
DU = 5.3516e+03

El sistema formado por los dos condensadores se conecta a una resistencia a la que suministra energía eléctrica i²·R. Donde

${\displaystyle i=\frac{1}{R}\left(\frac{q_1}{C_1}-\frac{q_2}{C_2}\right)=\frac{V_1-V_2}{R}}$

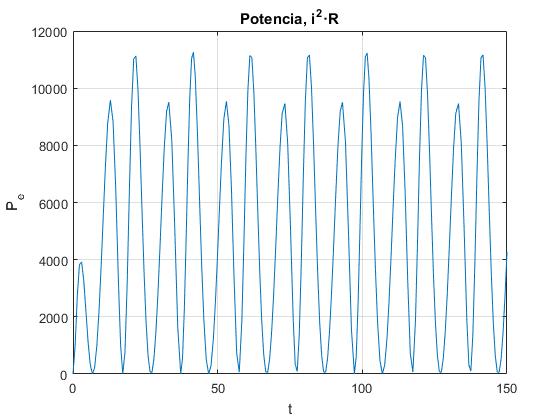
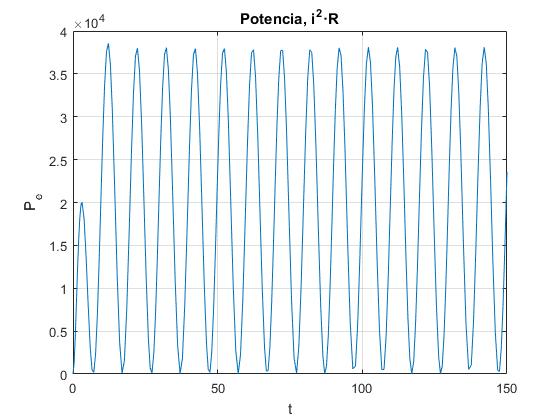
Añadimos al script el siguiente código para representar la potencia i²·R en función del tiempo t

.....
figure
plot(t,(V1-V2).^2/R)
grid on
xlabel('t')
ylabel('P_e');
title('Potencia, i^2·R')

La energía eléctrica suministrada por el sistema en el tiempo t es la integral

${\displaystyle W_e={\displaystyle \underset{0}{\overset{t}{\int }}{i}^{2}R\cdot dt}}$

Utilizamos la función de MATLAB trapz para calcular la integral (área bajo la curva) entre los instantes t=0 y t=150

>> We=trapz(t,(V1-V2).^2/R)
We = 7.2377e+05

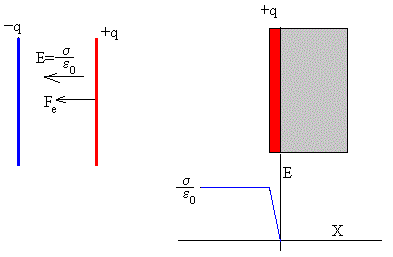
Imaginemos que la carga en la superficie de la placa ocupa una capa delgada, como se indica en la figura, el campo variará desde cero en la superficie interna de la capa hasta σ/ε₀, en el espacio entre las placas. Donde σ=q/S es la densidad de carga. El campo medio que actúa sobre la carga situada en la capa delgada es σ/(2ε₀) y por tanto, las fuerza F_e sobre la carga situada en la capa delgada es qσ/(2ε₀).

${\displaystyle F_e=\frac{1}{2}\frac{q^2}{\epsilon S}}$

Para mover las placas del primer condensador es necesario ejercer una fuerza F_m igual y de sentido contrario a F_e. El trabajo mecánico W_m de dicha fuerza en un tiempo t es

${\displaystyle W_m={\displaystyle \underset{0}{\overset{t}{\int }}{F}_{m}vdt}}$

donde v es la velocidad de desplazamiento de la placa del primer condensador v=Aωcos(ωt)

>> Fm=q1.^2/(2*eS);
>> Wm=trapz(t,Fm.*(A*w*cos(w*t)))
Wm =   7.3274e+05

La conservación de la energía se formula del siguiente modo: Una parte del trabajo mecánico realizado sobre las placas del primer condensador se disipa en la resistencia y otra parte, se acumula en los condensadores en forma de energía electrostática.

Calculamos el tanto por ciento de error al efectuar el cálculo numérico

${\displaystyle \left|\frac{W_m-W_e-\Delta U}{W_m}\right|100}$

>> abs((Wm-We-DU)/Wm)*100
ans =    0.4932

Actividades

Se introduce

• El periodo P de la oscilación de las placas del primer condensador, en el control titulado Periodo
• La fem V₀ de la batería que carga a los dos condensadores inicialmente iguales, en el control titulado ddp
• La resistencia R del circuito que une los dos condensadores, en el control titulado Resistencia

Observamos el movimiento periódico de las placas del primer condensador, la carga va cambiando con el tiempo, tal como se observa en los colores de las placas (rojo indica placa positiva), (azul placa negativa). Cuanto más intenso es el color más carga tiene la placa

El movimiento de los puntos de color rojo señala la corriente (portadores de carga positiva)

En la parte inferior derecha, se representa la potencia i²R disipada en la resistencia, en función del tiempo t.

Se proporciona los datos de la diferencia de potencial V₁ entre las placas del primer condensador C₁ y entre las placas V₂ del segundo.

La capacidad de los dos condensadores es variable

La placas del primer condensador C₁ son móviles de modo que la separación entre las mismas varía con el tiempo de la forma d₁=d+Asin(ωt). Su capacidad es variable

${\displaystyle C_1=\frac{\epsilon S}{d+A\sin (\omega t)}}$

Las placas del segundo condensador C₂ se mueven con la misma amplitud A, la misma frecuencia angular ω, pero en oposición de fase de modo que la separación entre las mismas es d₂=d-Asin(ωt). Su capacidad es

${\displaystyle C_2=\frac{\epsilon S}{d-A\sin (\omega t)}}$

La ecuación del circuito se escribe ahora

${\displaystyle \begin{array}{l}-R\frac{d{q}_1}{dt}+\left(Q-q_1\right)\frac{d-A\sin (\omega t)}{\epsilon S}-q_1\frac{d+A\sin (\omega t)}{\epsilon S}=0\\ \frac{d{q}_1}{dt}=\frac{1}{\epsilon SR}\left(-q_1\left(d+A\sin (\omega t)\right)+(Q-q_1)\left(d-A\sin (\omega t)\right)\right)\end{array}}$

Resolvemos la ecuación diferencial por procedimientos numéricos con las siguiente condición inicial, en el instante t=0, la carga del primer condensador es q₀₁.

Datos:

• Separación entre las placas del condensador, d=2
• Area de las placas del condensador, S=10
• Permitividad de la sustancia dieléctrica, ε=10;
• Resistencia del circuito, R=0.1
• Las separaciones d₁ y d₂ entre las placas de los condensadores, varía con el tiempo con una amplitud A=1 y un periodo P=20

${\displaystyle d_1=d+A\sin \left(\frac{2\pi }{P}t\right)d_2=d-A\sin \left(\frac{2\pi }{P}t\right)}$

• Inicialmente, t=0, los dos condensadores se cargan conectándolos a una batería de V₀=100 V, La carga inicial que adquieren cada uno de los dos condensadores, q₀₁=q₀₂ es

${\displaystyle q_{01}=V_0\frac{\epsilon S}{d}}$

A=1;  %amplitud
w=2*pi/20; %frecuencia angular
d=2;    %separación inicial
S=10; % area de las placas
epsilon=10; %permitividad
R=0.1; %resistencia
eS=epsilon*S;
V0=100; %fem de la batería que carga inicialmente los condensadores
Q=2*V0*eS/d;  %carga total

tspan=[0 150]; 
f=@(t,x) (-x*(d+A*sin(w*t))+(Q-x)*(d-A*sin(w*t)))/(eS*R);
[t,q1]=ode45(f,tspan,Q/2);

plot(t,q1, t, Q-q1)
grid on
legend('q_1','q_2')
xlabel('t')
ylabel('q_1, q_2');
title('Carga')

figure
V1=q1.*(d+A*sin(w*t))/eS;
V2=(Q-q1).*(d-A*sin(w*t))/eS;
plot(t,V1,t,V2)
grid on
legend('V_1','V_2')
xlabel('t')
ylabel('V_1, V_2');
title('ddp')

figure
plot(t,(V1-V2).^2/R)
grid on
xlabel('t')
ylabel('P_e');
title('Potencia, i^2·R')

Carga de cada uno de los condensadores q₁ y q₂ en función del tiempo t

Diferencia de potencial entre las placas de cada uno de los condensadores V₁ y V₂ en función del tiempo t

Representamos la potencia i²·R en función del tiempo t

Trabajo y energía

En el instante t=0, los condensadores cuyas capacidades son C₁=C₂=εS/d, han sido cargados poniéndolos en contacto con una batería de fem V₀, adquiriendo cargas q₀₁=q₀₂=V₀·(εS/d)

En el instante t, las cargas de los condensadores son q₁ y q₂=Q-q₁, sus capacidades son C₁=εS/(d+Asin(ωt)) y C₂=εS/(d-Asin(ωt))

La variación de energía eléctrostática ΔU=ΔU₁+ΔU₂ acumulada en los condensadores es

>> DU=q1(end)^2*(d+A*sin(w*t(end)))/(2*eS)+
(Q-q1(end))^2*(d-A*sin(w*t(end)))/(2*eS)-V0^2*eS/d
DU =   2.9468e+04

>> We=trapz(t,(V1-V2).^2/R)
We =   2.7720e+06

Ahora tenemos dos trabajos mecánicos, que se efectúan sobre las placas de los dos condensadores

>> F1=q1.^2/(2*eS);
>> F2=(Q-q1).^2/(2*eS);
>> Wm=trapz(t,F1.*(A*w*cos(w*t)))+trapz(t,F2.*(-A*w*cos(w*t)))
Wm =   2.8046e+06

>> abs((Wm-We-DU)/Wm)*100
ans =    0.1112

Actividades

Se introduce

• El periodo P de la oscilación de las placas del primer condensador, en el control titulado Periodo
• La fem V₀ de la batería que carga a los dos condensadores inicialmente iguales, en el control titulado ddp
• La resistencia R del circuito que une los dos condensadores, en el control titulado Resistencia

Observamos el movimiento periódico de las placas de los dos condensadores, la carga va cambiando con el tiempo, tal como se observa en los colores de las placas (rojo indica placa positiva), (azul placa negativa). Cuanto más intenso es el color más carga tiene la placa

El movimiento de los puntos de color rojo señala la corriente (portadores de carga positiva)

En la parte inferior derecha, se representa la potencia i²R disipada en la resistencia, en función del tiempo t.

Se proporciona los datos de la diferencia de potencial V₁ entre las placas del primer condensador C₁ y entre las placas V₂ del segundo.

El lector puede apreciar las ventajas del segundo sistema (placas de los dos condensadores oscilando en oposición de fase) frente al primero. Puede modificar el código MATLAB para valorar otras posibilidades, por ejemplo, que las frecuencias de las oscilaciones de las placas de los dos condensadores sean distintas, que el desfase entre las dos oscilaciones no sea π sino otro valor cualesquiera.

Referencias

Hiroshi Isshiki, Hideyuki Niizato. Conversion of Low Speed Mechanical Energy into Electric Energy - New Electrostatic Generator. Asian Journal of Engineering and Technology. Volume 02, Issue 04, August 2014, 320-331.