Modelo eléctrico del ciclo de Carnot

En esta página, se describe un modelo eléctrico del ciclo de Carnot, cuyo propósito es el de practicar con la relación q=C·V, entre las magnitudes

Carga q del condensador
Capacidad C
Diferencia de potencial V entre sus placas

Del mismo modo, que al estudiar los ciclos de térmicos, usamos la relación p·V=nRT de un gas ideal

Presión p del gas
Volumen V del recipiente
Temperatura absoluta T del gas

Como ya hicimos en el estudio del ciclo de Carnot, se calcula y se relaciona en cada una de las cuatro etapas de las que consta el ciclo.

La energía del condensador (similar a la energía interna)
El trabajo realizado al desplazar su placa móvil en contra de las fuerzas de atracción eléctrica.
La energía eléctrica (similar al calor) absorbida o cedida por el condensador cuando se conecta a las baterías.

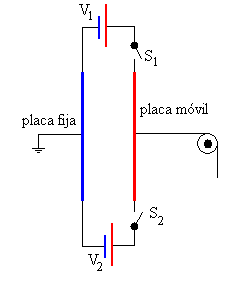
En la figura, se muestra el dispositivo eléctrico análogo al motor ideal de Carnot. La batería superior V₁ tiene un potencial mayor que la batería inferior V₂. Ambas representan dos focos de calor uno caliente a la temperatura T₁ y otro frío a la temperatura T₂, respectivamente.

La placa fija del condensador se conecta a los terminales negativos de las baterías y ésta a Tierra. Las cuatro etapas del ciclo son:

Se cierra el interruptor S₁ y se conecta el terminal positivo de la batería V₁ a la placa móvil.
Se abre el interruptor S₁
Se cierra el interruptor S₂ y se conecta el terminal positivo de la batería V₂ a la placa móvil
Se abre el interruptor S₂.

Etapas del ciclo

En primer lugar, recordamos la fórmula de la capacidad de un condensador plano-paralelo cuyas placas tienen un área S y están separadas una distancia d.

$C = \frac{ε_{0} S}{d}$

Situación inicial

Partimos de una situación inicial en el que las placas del condensador plano-paralelo de área S, están separadas una distancia d₁ y la placa móvil está conectada a la batería V₁. La carga q₁ del condensador será

$q_{1} = C \cdot V_{1} = \frac{V_{1}}{d_{1}} ε_{0} S$

La energía inicial del condensador es

$U_{i} = \frac{1}{2} C V_{1}^{2} = \frac{1}{2} ε_{0} S \frac{V_{1}^{2}}{d_{1}}$

1.-Proceso V=cte.

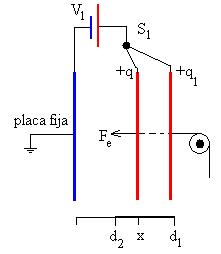
Se cierra el interruptor S₁ y se conecta el terminal positivo de la batería V₁ a la placa móvil. La separación entre las placas disminuye de d₁ a d₂. La carga aumenta de q₁ a q₂.

La carga q del condensador y su energía U cuando la separación entre las placas es x, d₂≤x≤d₁ son respectivamente

$q = ε_{0} S \frac{V_{1}}{x} U = \frac{1}{2} C V_{1}^{2} = \frac{1}{2} ε_{0} S \frac{V_{1}^{2}}{x}$

La fuerza F_e de atracción ente las placas cuando la diferencia de potencial V es constante es

$F_{e} = {(\frac{\partial U}{\partial x})}_{V} = - \frac{1}{2} ε_{0} S \frac{V_{1}^{2}}{x^{2}}$

El trabajo W realizado por la fuerza F_e es

$W = \int_{d_{1}}^{x} F_{e} \cdot d x = \frac{1}{2} ε_{0} S (\frac{1}{x} - \frac{1}{d_{1}}) V_{1}^{2}$

La batería V₁ suministra carga al condensador. Cuando el condensador está cargado con una carga q, la energía suministrada por la batería será

$Q = \int_{q_{1}}^{q} V_{1} d q = (q - q_{1}) \cdot V_{1}$

Cuando se termina la primera etapa x=d₂, la carga q₂ del condensador será

$q_{2} = C \cdot V_{1} = \frac{V_{1}}{d_{2}} ε_{0} S$

y la energía final U del condensador

$U = \frac{1}{2} C V_{1}^{2} = \frac{1}{2} ε_{0} S \frac{V_{1}^{2}}{d_{2}} = \frac{1}{2} \frac{q_{2}^{2}}{ε_{0} S} d_{2}$

La variación ΔU₁ de la energía del condensador es

$Δ U_{1} = \frac{1}{2} ε_{0} S (\frac{1}{d_{2}} - \frac{1}{d_{1}}) V_{1}^{2} > 0$

El trabajo W₁ realizado por la fuerza de atracción eléctrica F_e es

$W_{1} = \frac{1}{2} ε_{0} S (\frac{1}{d_{2}} - \frac{1}{d_{1}}) V_{1}^{2} > 0$

La energía Q₁ suministrada por la batería será

$Q_{1} = (q_{2} - q_{1}) V_{1} = ε_{0} S (\frac{1}{d_{2}} - \frac{1}{d_{1}}) V_{1}^{2} > 0$

La energía suministrada por la batería Q₁ se invierte en aumentar la energía del condensador ΔU₁ y en realizar un trabajo W₁.

Q₁= ΔU₁+ W₁.

2.-Proceso q=cte.

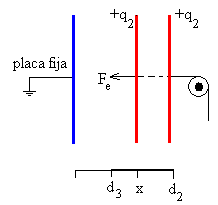
Se abre el interruptor S₁. La separación entre las placas disminuye de d₂ a d₃. La diferencia de potencial entre las placas disminuye de V₁ a V₂ mientras la carga de las placas permanece constante q₂.

Calculamos el valor de d₃ para que la diferencia de potencial entre las placas del condensador al terminar esta etapa sea V₂.

$q_{2} = ε_{0} S \frac{V_{2}}{d_{3}} d_{3} = \frac{V_{2}}{V_{1}} d_{2}$

La diferencia de potencial V entre las placas del condensador y su energía U cuando la separación entre las placas es x, d₃≤x≤d₂ son respectivamente

$V = \frac{q_{2}}{C} = \frac{q_{2} x}{ε_{0} S} U = \frac{1}{2} \frac{q_{2}^{2}}{C} = \frac{1}{2} \frac{q_{2}^{2}}{ε_{0} S} x$

La fuerza F_e de atracción ente las placas cuando la carga q es constante es

$F_{e} = - {(\frac{\partial U}{\partial x})}_{q} = - \frac{1}{2} \frac{q_{2}^{2}}{ε_{0} S}$

El trabajo W realizado por la fuerza F_e es

$W = \int_{d_{2}}^{x} F_{e} \cdot d x = - \frac{1}{2} \frac{q_{2}^{2}}{ε_{0} S} (x - d_{2})$

Cuando se termina la segunda etapa x=d₃, la carga del condensador es q₂ y la energía final es

$U = \frac{1}{2} \frac{q_{2}^{2}}{C} = \frac{1}{2} \frac{q_{2}^{2}}{ε_{0} S} d_{3} = \frac{1}{2} ε_{0} S \frac{V_{2}^{2}}{d_{3}}$

La variación de energía ΔU₂ del condensador será

$Δ U_{2} = \frac{1}{2} \frac{q_{2}^{2}}{ε_{0} S} (d_{3} - d_{2}) < 0$

El trabajo W₂ realizado por la fuerza de atracción eléctrica F_e es

$W_{2} = - \frac{1}{2} \frac{q_{2}^{2}}{ε_{0} S} (d_{3} - d_{2}) > 0$

Como vemos se cumple que ΔU₂+ W₂=0. La energía del condensador disminuye y se transforma en trabajo de la fuerza de atracción entre las placas.

3.-Proceso V=cte.

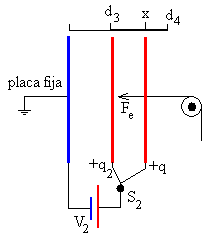
Se cierra el interruptor S₂ y se conecta el terminal positivo de la batería V₂ a la placa móvil. La separación entre las placas aumenta de d₃ a d₄. La carga disminuye de q₂ a q₁.

Calculamos el valor de d₄ para que la carga del condensador al terminar esta etapa sea q₁.

$q_{1} = ε_{0} S \frac{V_{2}}{d_{4}} d_{4} = \frac{V_{2}}{V_{1}} d_{1}$

La carga q del condensador y su energía U cuando la separación entre las placas es x, d₃≤x≤d₄ son, respectivamente

$q = ε_{0} S \frac{V_{2}}{x} U = \frac{1}{2} C V_{2}^{2} = \frac{1}{2} ε_{0} S \frac{V_{2}^{2}}{x}$

La fuerza F_e de atracción ente las placas cuando la diferencia de potencial V es constante es

$F_{e} = {(\frac{\partial U}{\partial x})}_{V} = - \frac{1}{2} ε_{0} S \frac{V_{2}^{2}}{x^{2}}$

El trabajo W realizado por la fuerza F_e es

$W = \int_{d_{1}}^{x} F_{e} \cdot d x = \frac{1}{2} ε_{0} S (\frac{1}{x} - \frac{1}{d_{3}}) V_{2}^{2}$

La batería V₂ retira carga del condensador. Cuando el condensador está cargado con una carga q, la energía cedida a la batería será

$Q = \int_{q 2}^{q} V_{2} d q = (q - q_{2}) \cdot V_{2}$

Cuando se termina la tercera etapa x=d₄, el condensador estará cargado con una carga q₁ y la energía final U del condensador

$U = \frac{1}{2} C V_{2}^{2} = \frac{1}{2} ε_{0} S \frac{V_{2}^{2}}{d_{4}} = \frac{1}{2} \frac{q_{1}^{2}}{ε_{0} S} d_{4}$

La variación ΔU₃ de la energía del condensador es

$Δ U_{3} = \frac{1}{2} ε_{0} S (\frac{1}{d_{4}} - \frac{1}{d_{3}}) V_{2}^{2} < 0$

El trabajo W₃ realizado por la fuerza de atracción eléctrica F_e es

$W_{3} = \frac{1}{2} ε_{0} S (\frac{1}{d_{4}} - \frac{1}{d_{3}}) V_{2}^{2} < 0$

La energía Q₃ cedida a la batería será

$Q_{3} = (q_{1} - q_{2}) V_{2} = ε_{0} S (\frac{1}{d_{4}} - \frac{1}{d_{3}}) V_{2}^{2} < 0$

La energía cedida a la batería Q₃ proviene de la energía del condensador ΔU₃ y del trabajo W₃.

Q₃= ΔU₃+ W₃.

4.-Proceso q=cte.

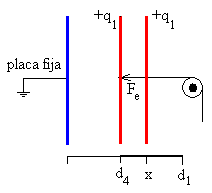
Se abre el interruptor S₂. La separación entre las placas aumenta de d₄ a d₁. La diferencia de potencial entre las placas aumenta de V₂ a V₁ mientras la carga de las placas permanece constante q₁.

La diferencia de potencial V entre las placas del condensador y su energía U cuando la separación entre las placas es x, d₄≤x≤d₁ son, respectivamente

$V = \frac{q_{2}}{C} = \frac{q_{1} x}{ε_{0} S} U = \frac{1}{2} \frac{q_{1}^{2}}{C} = \frac{1}{2} \frac{q_{1}^{2}}{ε_{0} S} x$

La fuerza F_e de atracción ente las placas (enlace) cuando la carga q es constante es

$F_{e} = - {(\frac{\partial U}{\partial x})}_{q} = - \frac{1}{2} \frac{q_{1}^{2}}{ε_{0} S}$

El trabajo W realizado por la fuerza F_e es

$W = \int_{d_{2}}^{x} F_{e} \cdot d x = - \frac{1}{2} \frac{q_{2}^{2}}{ε_{0} S} (x - d_{4})$

Cuando se termina la cuarta etapa x=d₁, la carga del condensador es q₁ y la energía final es

$U = \frac{1}{2} \frac{q_{1}^{2}}{C} = \frac{1}{2} \frac{q_{1}^{2}}{ε_{0} S} d_{1} = \frac{1}{2} ε_{0} S \frac{V_{1}^{2}}{d_{1}}$

La variación de energía ΔU₄ del condensador será

$Δ U_{4} = \frac{1}{2} \frac{q_{1}^{2}}{ε_{0} S} (d_{1} - d_{4}) > 0$

El trabajo W₄ realizado por la fuerza de atracción eléctrica F_e es

$W_{4} = - \frac{1}{2} \frac{q_{1}^{2}}{ε_{0} S} (d_{1} - d_{4}) < 0$

Como vemos se cumple que ΔU₄+ W₄=0. La energía del condensador aumenta a costa del trabajo de la fuerza de atracción entre las placas.

El ciclo completo

Los datos del ciclo son los potenciales de las baterías V₁, V₂ y las distancias d₁ y d₂ entre las placas del condensador plano-paralelo.

Variación de energía del condensador

Comprobamos que la variación de energía del condensador en el ciclo completo es cero

ΔU= ΔU₁ +ΔU₂ +ΔU₃ +ΔU₄=0

Para ello expresamos todos los términos en función de los datos V₁, V₂, d₁ y d₂.

$\begin{array}{l} Δ U_{1} = \frac{1}{2} ε_{0} S (\frac{1}{d_{2}} - \frac{1}{d_{1}}) V_{1}^{2} > 0 \\ Δ U_{2} = \frac{1}{2} ε_{0} S \frac{V_{1}}{d_{2}} (V_{2} - V_{1}) < 0 \\ Δ U_{3} = \frac{1}{2} ε_{0} S (\frac{1}{d_{1}} - \frac{1}{d_{2}}) V_{1} V_{2} < 0 \\ Δ U_{4} = \frac{1}{2} ε_{0} S \frac{V_{1}}{d_{1}} (V_{1} - V_{2}) > 0 \end{array}$

Trabajo total

Expresamos todas las contribuciones al trabajo en función de V₁, V₂, d₁ y d₂.

$\begin{array}{l} W_{1} = \frac{1}{2} ε_{0} S (\frac{1}{d_{2}} - \frac{1}{d_{1}}) V_{1}^{2} > 0 \\ W_{2} = \frac{1}{2} ε_{0} S \frac{V_{1}}{d_{2}} (V_{1} - V_{2}) > 0 \\ W_{3} = \frac{1}{2} ε_{0} S (\frac{1}{d_{1}} - \frac{1}{d_{2}}) V_{1} V_{2} < 0 \\ W_{4} = \frac{1}{2} ε_{0} S \frac{V_{1}}{d_{1}} (V_{2} - V_{1}) < 0 \end{array}$

El trabajo total

W= W₁ +W₂ +W₃ +W₄

$W = ε_{0} S V_{1} (V_{1} - V_{2}) (\frac{1}{d_{2}} - \frac{1}{d_{1}}) > 0$

La energía Q₁ absorbida por condensador de la batería que está al potencial V₁ es

$Q_{1} = ε_{0} S (\frac{1}{d_{2}} - \frac{1}{d_{1}}) V_{1}^{2} > 0$

La energía Q₃cedida por el condensador a la batería que está a potencial V₂ es

$Q_{3} = ε_{0} S (\frac{1}{d_{1}} - \frac{1}{d_{2}}) V_{1} V_{2} < 0$

Verificamos que Q₁+Q₃=W

Parte la energía Q₁ proporcionada por la batería a potencial V₁ se emplea en realizar un trabajo W y la otra parte, |Q₃| se cede a la batería que está a un potencial más bajo V₂.

El rendimiento del ciclo es

$η = \frac{W}{Q_{1}} = 1 - \frac{V_{2}}{V_{1}}$

Actividades

Se introduce

El potencial V₁ de la batería superior, en el control titulado Potencial V₁.
El potencial V₂ de la batería inferior, en el control titulado Potencial V₂.
La distancia d₁ inicial entre las placas del condensador está fijada en el programa en el valor d₁=10.0
La distancia d₂ se puede cambiar entre los valores 3.0 y 9.0, en el control titulado Posición d₂.

Se pulsa el botón titulado Nuevo

Se tendrá que cumplir que V₁>V₂. En el caso de que V₁ sea inferior a V₂ el programa no prosigue y nos invita a modificar bien V₂ o V₁.

Al lado de la placa derecha, se dan los valores de

La carga q del condensador (abajo)
La diferencia de potencial V entre sus placas (arriba).

Al lado de la placa izquierda, se proporciona los datos de

La energía Q₁ suministrada por la batería superior (arriba)
La energía U del condensador cargado (en medio)
La energía Q₃ cedida a la batería inferior (abajo)

Un diagrama de barras en la parte derecha nos proporciona, para cada una de las etapas

La variación de la energía del condensador ΔU (en rojo)
El trabajo W realizado por las fuerzas de atracción eléctrica entre las placas (en azul)
La energía Q suministrada por la batería superior (positiva) o cedida a la inferior (negativa) en color gris.

Los datos se dan en un sistema de unidades en el que el producto ε₀S=1.

Ejemplo:

ddp de la batería superior, V₁=500.0
ddp de la batería inferior, V₂=300.0
La distancia inicial entre las placas es d₁=10.0
Introducimos la distancia d₂ entre las placas, d₂=7.0

Calculamos los valores de d₃=4.2 y d₄=6.0 y las cargas del condensador en la primera y tercera etapa q₁=50.0, q₂=71.4

Etapa	Variación de energía ΔU	Trabajo W	Batería Q
Primera, V₁=cte	5357.1	5357.1	10714.3
Segunda, q₂=cte	-7142.9	7142.9	0
Tercera, V₂=cte	-3214.3	-3214.3	-6428.6
Cuarta, q₁=cte	5000	-5000	0
Total	0	4285.7	4285.7

Rendimiento

$η = \frac{4285.7}{10714.3} = 0.4 η = 1- \frac{300}{500} = 0.4$

Potencial V₁<1000: Potencial V₂>100:
Posición:

Referencias

Chen Minghua. An electrical model of a Carnot cycle. The Physics Teacher. April 1989, pp. 272-273.