Fuerza de atracción entre las placas de un condensador

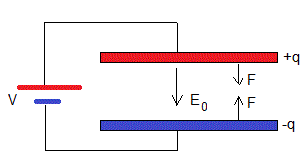
Sea un condensador plano-paralelo, cuyas placas tiene un área S y están separadas una distancia d. La capacidad del condensador es C=ε₀S/d

Se conecta el condensador a una batería. Las placas del condensador se cargan con cargas iguales y opuestas +q y -q. q=CV

Entre las placas del condensador existe un campo eléctrico E₀=σ/ε₀. El campo eléctrico ejerce una fuerza F sobre la carga de la placa. Su valor contrariamente a lo que cabría suponer no es qE₀, precisamos de un análisis más detallado.

Para ello, nos fijaremos en la placa positiva, que ampliaremos en la siguiente figura

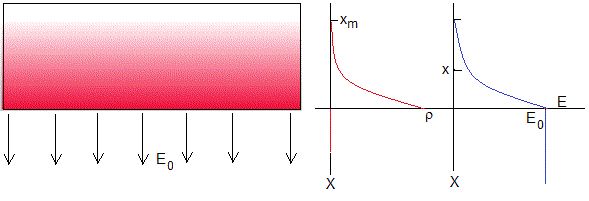
Hemos estudiado que el campo en el interior de un conductor es cero y la carga está situada en la superficie del conductor.

En realidad, el campo pasa de cero a un valor constante E₀ de forma continua, ya que la carga q reside en las proximidades de la superficie del conductor.

Supongamos que la densidad de carga ρ(x) disminuye rápidamente desde la superficie de la placa hacia su interior de la forma que indica la curva del color rojo, o el gradiente de color rojo con el que se ha pintado la placa

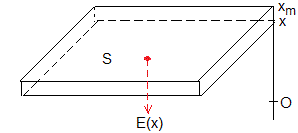
Conocida la densidad de carga, aplicamos la ley de Gauss para determinar el campo eléctrico en la posición x en el interior de la placa. Consideremos una superficie cerrada en forma de prisma de la figura. En el interior del conductor, en x_m el campo eléctrico es cero E(x_m)=0. Solamente hay flujo a través de la cara inferior situada en x. La ley de Gauss se escribe

${\displaystyle E(x)S=\frac{1}{{\epsilon }_0}{\displaystyle \underset{x_m}{\overset{x}{\int }}\rho (x)S·dx}}$

siendo ρ(x)S·dx la carga existente en la lámina de área S comprendida entre x y x+dx

El campo eléctrico E(x) se obtiene integrando la densidad de carga ρ(x) y la densidad de carga se obtiene derivando el campo eléctrico

${\displaystyle \rho (x)={\epsilon }_0\frac{dE(x)}{dx}}$

La fuerza que ejerce el campo eléctrico E(x) sobre dicha lámina de carga es

${\displaystyle dF=E(x)·\rho (x)S·dx}$

La fuerza total es

${\displaystyle F={\displaystyle \underset{x_m}{\overset{0}{\int }}E(x)S\rho (x)}dx=S{\epsilon }_0{\displaystyle \underset{x_m}{\overset{0}{\int }}E(x)\frac{dE(x)}{dx}}dx=S{\epsilon }_0{\frac{E^2(x)}{2}|}_{x_m}^0=\frac{1}{2}S{\epsilon }_0{E}_0^2}$

Otras formas de expresar la fuerza F para un condensador plano-paralelo son

${\displaystyle F=\frac{1}{2}{\epsilon }_{0}S\frac{V^2}{d^2}=\frac{1}{2}\frac{q^2}{{\epsilon }_{0}S}}$

Electrómetro de placas

Carga constante

Conectamos un condensador plano-paralelo a una batería que carga las placas del condensador con una carga q. A continuación, desconectamos la batería.

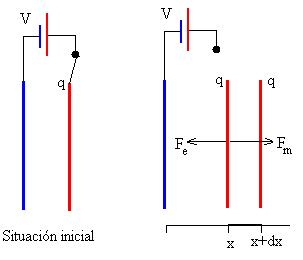
Supongamos que la separación entre las placas del condensador es x y mediante una fuerza mecánica externa F_m igual y opuesta a la fuerza de atracción electrostática F_e aumentamos la separación entre las placas en dx.

El trabajo dW_m=F_m·dx realizado por la fuerza mecánica se invierte en modificar la energía U=q²/(2C) almacenada por el condensador en forma de campo eléctrico. Como la batería está desconectada no suministra ninguna energía al condensador durante este proceso, por lo que dW_m=dU

${\displaystyle F_m={\left(\frac{\partial U}{\partial x}\right)}_q=-\frac{q^2}{2C^2}\frac{dC}{dx}}$

Para un condensador plano-paralelo ideal C=ε₀·S/x, la fuerza vale

${\displaystyle F_m=\frac{q^2}{2{\epsilon }_{0}S}}$

Cuando la placa del condensador se desplaza Δx la capacidad disminuye, la energía del condensador aumenta

${\displaystyle \Delta U_c=\frac{1}{2}\frac{q^2}{C\text{'}}-\frac{1}{2}\frac{q^2}{C}=\frac{q^2}{2}\frac{x+\Delta x}{{\epsilon }_{0}S}-\frac{q^2}{2}\frac{x}{{\epsilon }_{0}S}=\frac{q^2}{2}\frac{\Delta x}{{\epsilon }_{0}S}}$

El trabajo realizado por la fuerza exterior F_m=F_e para incrementar la separación de las placas es

${\displaystyle W_m={\displaystyle \underset{x}{\overset{x+\Delta x}{\int }}\frac{1}{2}\frac{q^2}{{\epsilon }_{0}S}dx}=\frac{1}{2}\frac{q^2}{{\epsilon }_{0}S}(x+\Delta x-x)=\frac{q^2}{2}\frac{\Delta x}{{\epsilon }_{0}S}}$

El trabajo realizado por la fuerza exterior F_m se emplea en incrementar la energía ΔU_c del condensador

Potencial constante

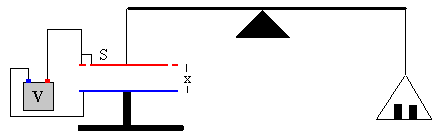
Las placas del condensador se ponen en contacto con una fuente ajustable de alto voltaje, que va variando poco a poco hasta que la balanza se pone en equilibrio. Un anillo metálico que rodea a la placa superior minimiza los efectos del campo que sale por los bordes de las placas paralelas. Para aislar el dispositivo de posibles influencias externas se coloca dentro de una caja metálica (jaula de Faraday)

Vamos a determinar la fuerza F_e de atracción entre las placas, suponiendo que el condensador tiene inicialmente una capacidad C y las placas están cargadas con una carga q tal que q=C·V

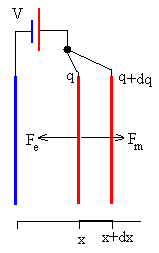
Incrementamos en dx la separación entre las placas ejerciendo una fuerza mecánica exterior F_m sobre la placa móvil igual y opuesta a la fuerza de atracción eléctrica F_e entre las placas.

El trabajo realizado por la fuerza mecánica es dW_m=F_m·dx

Si las placas del condensador se mantienen a una diferencia de potencial constante V mediante una batería, al modificarse la capacidad, la batería realiza un trabajo para suministrar o retirar una carga dq=V·dC. Este trabajo vale

dW_V=V·dq=V²·dC

El trabajo total realizado sobre el condensador modifica la energía U=CV²/2 almacenada en el mismo en forma de campo eléctrico.

dU= dW_V+ dW_m

Como V es constante, tenemos que

½V²·dC=V²·dC+F_m·dx

Despejamos la fuerza F_m

${\displaystyle F_m=-\frac{V^2}{2}{\left(\frac{dC}{dx}\right)}_V}$

Para un condensador plano-paralelo ideal C=ε₀·S/x

${\displaystyle F_m=\frac{{\epsilon }_{0}S{V}^2}{2}\frac{1}{x^2}}$

La fuerza de atracción entre las placas F_e=-F_m es inversamente proporcional al cuadrado de su separación x. Obtenemos la fuerza F_e, a partir de la energía U=CV²/2 almacenada en forma de campo eléctrico en el condensador, mediante la expresión.

${\displaystyle F_e={\left(\frac{\partial U}{\partial x}\right)}_V}$

Cuando la placa del condensador se desplaza Δx la capacidad disminuye, la energía del condensador disminuye.

${\displaystyle \Delta U_c=\frac{1}{2}C\text{'}{V}^2-\frac{1}{2}C{V}^2=\frac{1}{2}\frac{{\epsilon }_{0}S}{x+\Delta x}{V}^2-\frac{1}{2}\frac{{\epsilon }_{0}S}{x}{V}^2=-\frac{1}{2}\frac{\Delta x}{x(x+\Delta x)}{\epsilon }_{0}S{V}^2}$

El trabajo de la fuerza F_m es

${\displaystyle W_m={\displaystyle \underset{x}{\overset{x+\Delta x}{\int }}\frac{1}{2}\frac{S{\epsilon }_0}{x^2}{V}^{2}dx}=\frac{1}{2}S{\epsilon }_0{V}^2\left(\frac{1}{x}-\frac{1}{x+\Delta x}\right)=\frac{1}{2}S{\epsilon }_0{V}^2\left(\frac{\Delta x}{x(x+\Delta x)}\right)}$

A medida que se separa las placas, decrece la capacidad, las placas pierden carga que va a la batería.

${\displaystyle \Delta q=C\text{'}V-CV=\frac{{\epsilon }_{0}S}{x+\Delta x}V-\frac{{\epsilon }_{0}S}{x}V=-{\epsilon }_{0}SV\frac{\Delta x}{x(x+\Delta x)}}$

El trabajo realizado sobre la batería es el producto de la pérdida de carga que experimenta el condensador por la ddp V de la batería

${\displaystyle W_b=\left|\Delta q\right|V=-{\epsilon }_{0}S{V}^2\frac{\Delta x}{x(x+\Delta x)}}$

La batería gana energía que proviene, la mitad, de la disminución de la energía condensador ΔU_c y la otra mitad, del trabajo realizado por la fuerza externa W_m.

Actividades

El programa interactivo se trata de medir una tensión desconocida V, mediante un electrómetro formado por dos placas planas y paralelas.

La diferencia de potencial V se calcula midiendo la fuerza F entre las placas, conocidos los datos de la distancia x entre las placas y el área S de las mismas. El programa ha fijado:

• La separación entre placas, x=2 mm=0.002 m
• El radio de la placa circular en 10 cm, de modo que S=π(0.1)²

Cuando se pulsa el botón titulado Nuevo, se genera un número aleatorio que representa la tensión V desconocida de una batería.

Cuando se pulsa el botón titulado Conectar, las placas del condensador se conectan a dicha batería, atrayéndose entre sí. La balanza se desequilibra ya que su brazo está unido a la placa superior del condensador y tenemos que volverla a equilibrar para medir la fuerza de atracción F.

Moviendo los cursores de la balanza (de color azul, rojo y negro) equilibramos la balanza y medimos la fuerza en miligramos.

Ejemplo:

Equilibramos la balanza desplazando con el puntero del ratón los cursores hasta marcar 22.1 mg.

Sabiendo que el radio de las placas circulares es 10 cm y que su separación es de 2 mm. Introducimos los datos en la fórmula de la fuerza en las unidades adecuadas.

${\displaystyle 22.1\cdot {10}^{-6}\cdot 9.8=\frac{\pi ·{0.1}^2\cdot V^2}{4\pi 9\cdot {10}^9\cdot 2\cdot {0.002}^2}V=79.0\text{V}}$

Electrómetro cilíndrico

Si el cilindro interior no está completamente introducido en el exterior, sino solamente una longitud x, la capacidad del condensador será

${\displaystyle C=\frac{2\pi {\epsilon }_{0}x}{\ln (b/a)}}$

La energía del condensador es U=CV²/2. La fuerza que actúa sobre el cilindro interior del condensador, manteniendo constante el potencial V entre sus placas es

${\displaystyle F={\left(\frac{\partial U}{\partial x}\right)}_V=\frac{2\pi {\epsilon }_0}{\ln (b/a)}{V}^2}$

La fuerza es constante e independiente de x.

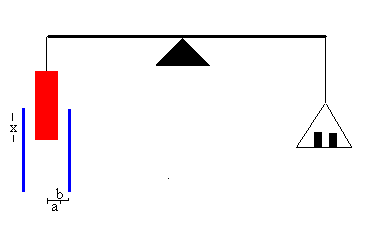
Actividades

Se trata de medir una tensión desconocida V, mediante un electrómetro formado por dos armaduras cilíndricas de radios a y b que tienen el mismo eje.

El potencial V se calcula midiendo la fuerza F, conocidos los datos del radio interior a y el radio exterior b del condensador cilíndrico.

Cuando se pulsa el botón titulado Nuevo, se genera un número aleatorio que representa la tensión V desconocida de un generador.

Cuando se pulsa el botón titulado Conectar, las placas del condensador se conectan a dicho generador. El cilindro interior es atraído por el campo eléctrico y la balanza se desequilibra. Tenemos que volverla a equilibrar para medir la fuerza de atracción F.

Moviendo los cursores (flechas de color azul, rojo y negro) equilibramos la balanza y medimos la fuerza en miligramos.

Ejemplo:

Equilibramos la balanza desplazando con el puntero del ratón los cursores hasta marcar 57.7 mg.

Sabiendo que el radio interior a del cilindro es de 45 mm y el radio del cilindro exterior es de 50 mm. Introducimos los datos en la fórmula de la fuerza en las unidades adecuadas.

${\displaystyle 57.7\cdot {10}^{-6}\cdot 9.8=\frac{\pi \cdot V^2}{4\pi 9\cdot {10}^9\cdot \ln \frac{50}{45}}V=1464.5}$

Referencias

Bernhard Jakoby. On the origin and calculation of the force in electrostatic actuators. Eur. J. Phys. 37 (2016) 045207

Feynman R. Leighton, Sands . The Feynman lectures on Physics on physics. Vol II Electromagnetismo y materia, 8-2, Fondo Educativo Interamericano 1972.

Greene N. R. Energy flow for a variable-gap capacitor. The Physics Teacher, Vol 43, September 2005, pp. 340-343