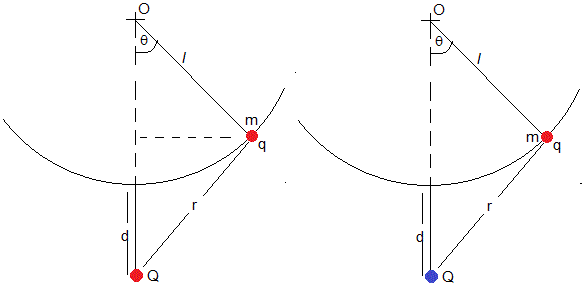
El sistema está formado por una partícula de masa m y carga q unida a un hilo inextensible de longitud l. A una distancia d por debajo de la posición θ=0 hay una carga fija Q que puede ser positiva (color rojo) o negativa (color azul).

Equilibrio y estabilidad

La energía potencial tiene dos contribuciones: la energía potencial gravitatoria y la energía potencia correspondiente a la interacción entre las dos cargas. Cuando la posión angular del péndulo es θ, las distancia entre las cargas es r

${\displaystyle \begin{array}{l}{E}_p=-mgl\cos \theta +\frac{1}{4\pi {\epsilon }_0}\frac{qQ}{r}\\ E_p=-mgl\cos \theta +\frac{qQ}{4\pi {\epsilon }_0}\frac{1}{\sqrt{{\left(l+d\right)}^2+l^2-2\left(l+d\right)l\cos \theta }}\\ E_p=-mgl\cos \theta +\frac{qQ}{4\pi {\epsilon }_0\sqrt{2\left(l+d\right)l}}\frac{1}{\sqrt{\frac{{\left(l+d\right)}^2+l^2}{2\left(l+d\right)l}-\cos \theta }}\end{array}}$

Expresamos la energía potencial por unidad de masa, en términos de dos parámetros, b y c

${\displaystyle \begin{array}{l}\frac{E_p(\theta )}{m}=-gl\cos \theta +\frac{b}{\sqrt{c-\cos \theta }}\\ k=\frac{qQ}{4\pi {\epsilon }_{0}m},b=\frac{k}{\sqrt{2\left(l+d\right)l}},c=\frac{{\left(l+d\right)}^2+l^2}{2\left(l+d\right)l}\end{array}}$

El parámetro c>1, ya que $\frac{a^2+b^2}{2ab}>1$. El parámetro k y por tanto, b es positivo, si las cargas son del mismo signo y negativo si son de signo contrario

Las posiciones de equilibrio son

${\displaystyle \frac{d{E}_p}{d\theta }=gl\sin \theta -\frac{b\sin \theta }{2{\left(c-\cos \theta \right)}^{3/2}}=\mathrm{0,}\{\begin{array}{l}\sin \theta =\mathrm{0,}\theta =\mathrm{0,}\pi \\ \cos \theta =c-{\left(\frac{b}{2gl}\right)}^{2/3}\end{array}}$

Para determinar si estas psiciones son estables (mínimo) o inestables (máximo), calculamos la derivada segunda

${\displaystyle \frac{d^2{E}_p}{d{\theta }^2}=gl\cos \theta -\frac{b}{2}\frac{c\cos \theta -1-\frac{1}{2}{\sin }^2\theta }{{\left(c-\cos \theta \right)}^{5/2}}}$

• Para k<0 ó b<0 (cargas de distinto signo)

Representamos la función energía potencial para, k=-1, la distancia entre las cargas para θ=0 es d=0.2 m, la longitud del péndulo es l=1 m



• Para θ=0 (mínimo), estable

${\displaystyle gl-\frac{b}{2}\frac{1}{{\left(c-1\right)}^{3/2}}>\mathrm{0,}b<0}$

• Para θ=π (máximo), inestable

${\displaystyle -gl+\frac{b}{2}\frac{1}{{\left(c+1\right)}^{3/2}}<\mathrm{0,}b<0}$

• Para k>0 ó b>0 (cargas del mismo signo)

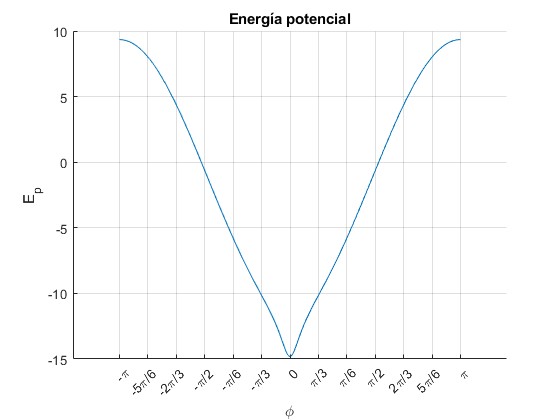
Representamos la función energía potencial para, k=1, la distancia entre las cargas para θ=0 es d=0.6 m, la longitud del péndulo es l=1 m



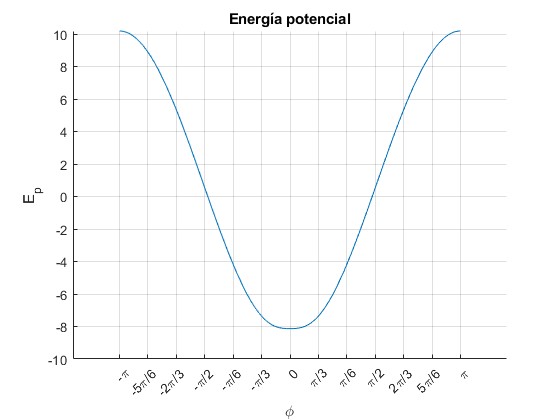
Representamos la función energía potencial para, k=1, la distancia entre las cargas para θ=0 es d=0.1 m, la longitud del péndulo es l=1 m



• Para θ=0

${\displaystyle {\left(\frac{d^2{E}_p}{d{\theta }^2}\right)}_{\theta =0}=gl-\frac{b}{2}\frac{1}{{\left(c-1\right)}^{3/2}},b>0}$

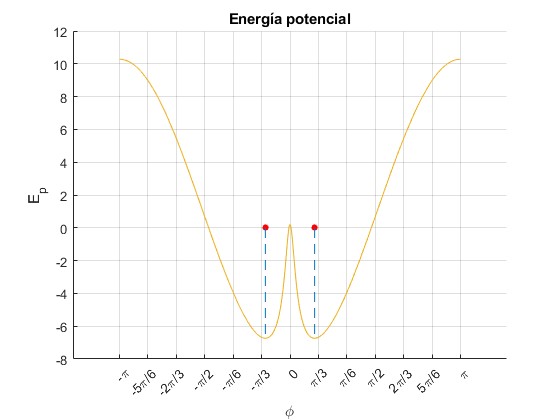
Fijada la longitud del péndulo l=1 y el parámetro k=1, existe una distancia crítica d_c, por debajo de la cual d<d_c la posición θ=0, es inestable y por encima d>d_c, es estable. Véase las dos figuras

${\displaystyle \begin{array}{l}gl-\frac{k}{2\sqrt{2\left(l+d\right)l}}\frac{1}{{\left(\frac{{\left(l+d\right)}^2+l^2}{2\left(l+d\right)l}-1\right)}^{3/2}}=0\\ gl-\frac{k}{2\sqrt{2\left(l+d\right)l}}\frac{1}{{\left(\frac{{\left(l+d\right)}^2+l^2}{2\left(l+d\right)l}-1\right)}^{3/2}}=0\\ gl-k\frac{l(l+d)}{d^3}=0\\ g{d}^3-kd-kl=0\end{array}}$

La distancia crítica es la raíz real positiva de la ecuación cúbica, d_c= 0.5396 m

>> l=1;
>> k=1;
>> roots([9.8,0,-k,-k*l])
ans =
   0.5396 + 0.0000i
  -0.2698 + 0.3411i
  -0.2698 - 0.3411i

• Para θ=π

${\displaystyle {\left(\frac{d^2{E}_p}{d{\theta }^2}\right)}_{\theta =\pi }=-gl+\frac{b}{2}\frac{1}{{\left(c+1\right)}^{3/2}},b>0}$

Fijada la longitud del péndulo l=1 y el parámetro k=1, buscamos una nueva distancia crítica d_c.

${\displaystyle \begin{array}{l}-gl+\frac{k}{2\sqrt{2\left(l+d\right)l}}\frac{1}{{\left(\frac{{\left(l+d\right)}^2+l^2}{2\left(l+d\right)l}+1\right)}^{3/2}}=0\\ gl-k\frac{l(l+d)}{{\left(2l+d\right)}^3}=0\\ d^3+6l{d}^2+\left(12l^2-\frac{k}{g}\right)d+8l^3-\frac{k}{g}l=0\end{array}}$

>> l=1;
>> k=1;
>> roots([1,6*l, (12*l^2-k/9.8),8*l^3-k*l/9.8])
ans =
  -2.5396 + 0.0000i
  -1.7302 + 0.3411i
  -1.7302 - 0.3411i

No hay raíz real positiva de la ecuación cúbica. La posición θ=π corresponde a un máximo (inestable), como se aprecia en las representaciones gráficas

• Para d<d_c hay dos posiciones angulares dadas por la ecuación, $\cos \theta =c-{\left(\frac{b}{2gl}\right)}^{2/3}$,iguales pero de signo contrario, señaladas por dos puntos de color rojo en la figura

No ha sido posible demostrar que ambas corresponden a mínimos de la energía potencial (posiciones de equilibrio estable), tal como se aprecia en las figuras

El código para representar las dos figuras anteriores es el siguiente

l=1; %longitud del péndulo
d=0.1; %distancia entre cargas para th=0
k=1; %parámetro
b=k/sqrt(2*(l+d)*l);
c=((l+d)^2+l^2)/(2*(l+d)*l);
hold on
if k>0
    rr=roots([9.8,0,-k,-k]);
    for r=rr'
        if isreal(r)
            d_c=r;
            break;
        end
    end
    if d<d_c
        th_1=acos(c-(b/(2*9.8*l))^(2/3));
        plot(th_1,0,'ro','markersize',4,'markerfacecolor','r')
        plot(-th_1,0,'ro','markersize',4,'markerfacecolor','r')
        line([th_1,th_1],[0,f(th_1)],'lineStyle','--')
        line([-th_1,-th_1],[0,f(th_1)],'lineStyle','--')
    end
end
f=@(x) -9.8*l*cos(x)+b./sqrt(c-cos(x));
fplot(f,[-pi,pi]) 
set(gca,'XTick',-pi:pi/6:pi)
set(gca,'XTickLabel',{'-\pi', '-5\pi/6','-2\pi/3','-\pi/2','-\pi/6','-\pi/3',
'0','\pi/3','\pi/6','\pi/2','2\pi/3','5\pi/6','\pi'})
hold off
grid on
xlabel('\phi')
ylabel('E_p')
title('Energía potencial')

Ecuación del movimiento

La energía cinética de la partícula es

${\displaystyle E_k=\frac{1}{2}m{v}^2=\frac{1}{2}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2}$

La energía potencial

${\displaystyle E_p(\theta )=-mgl\cos \theta +m\frac{b}{\sqrt{c-\cos \theta }}}$

Como las fuerzas sobre la partícula de masa m y carga q son conservativas, la energía permanece constante

${\displaystyle \frac{E}{m}=\frac{1}{2}{l}^2{\left(\frac{d\theta }{dt}\right)}^2-gl\cos \theta +\frac{b}{\sqrt{c-\cos \theta }}}$

La lagrangiana es

${\displaystyle \begin{array}{l}L=E_k-E_p\\ L=\frac{1}{2}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2+mgl\cos \theta -m\frac{b}{\sqrt{c-\cos \theta }}\end{array}}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ l^2\frac{d^2\theta }{d{t}^2}+gl\sin \theta -\frac{b\sin \theta }{2{\left(c-\cos \theta \right)}^{3/2}}=0\\ \frac{d^2\theta }{d{t}^2}+\frac{g}{l}\sin \theta -\frac{b}{2l^2}\frac{\sin \theta }{{\left(c-\cos \theta \right)}^{3/2}}=0\end{array}}$

El caso más interesante se produce cuando k=1, (cargas del mismo signo) y d<d_c, la distancia entre las cargas es menor que la crítica

Estudiamos el caso

• La longitud del pendulo, l=1 m
• El parámetro k=1 (cargas del mismo signo)
• Distancia crítica, d_c=0.5396 m
• Distancia entre las cargas para θ=0, d=0.1 m
• Posición inicial θ₀=π/3 (60°)
• Velocidad angular inicial, (dθ/dt)₀=0

La energía de la partícula es, E/m=-3.9508

La energía potencial para θ=0, es E_p(0)=0.2

La partícula oscila alrededor de la posición de equilibrio estable,

${\displaystyle {\theta }_1=\arccos \left(c-{\left(\frac{b}{2gl}\right)}^{2/3}\right)}$

θ₁=26°, señalada por una recta horizontal en la figura

Resolvemos la ecuación diferencial con las condiciones iniciales especificadas, por el procedimiento ode45 de MATLAB

l=1; %longitud del péndulo
d=0.1; %distancia entre cargas para th=0
k=1; %parámetro
b=k/sqrt(2*(l+d)*l);
c=((l+d)^2+l^2)/(2*(l+d)*l);
tf=2*2*pi/sqrt(9.8/l);
th_1=acos(c-(b/(2*9.8*l))^(2/3));
f=@(t,x) [x(2);-9.8*sin(x(1))/l+b*sin(x(1))/(2*l^2*(c-cos(x(1)))^(3/2))]; 
[t,x]=ode45(f,[0,tf],[pi/3,0]);
plot(t,x(:,1))
line([0,tf],[th_1,th_1])
grid on
ylabel('\phi')
xlabel('t')
title('Movimiento')

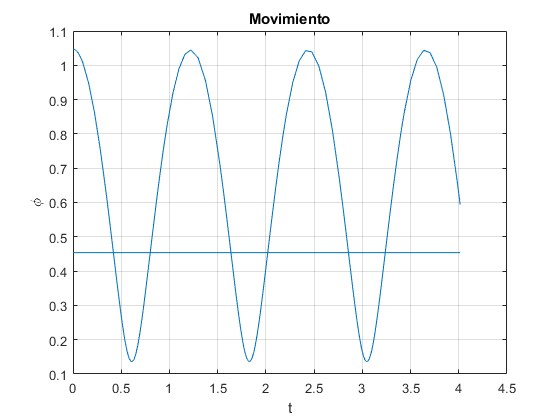
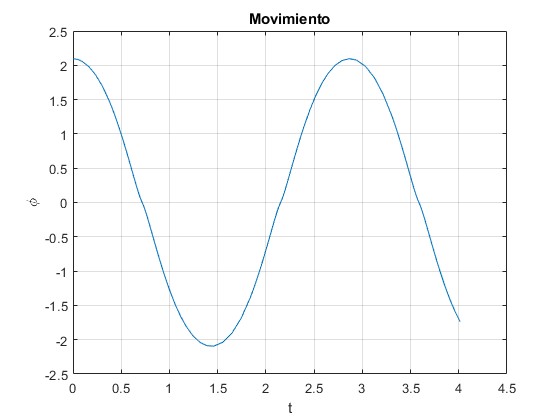
Cambiamos la posición inicial θ₀=2π/3 (120°)

La energía de la partícula es, E/m= 5.4496, mayor que E_p(0)=0.2

La partícula oscila alrededor de la posición de equilibrio estable θ=0, tal como se aprecia en la figura

Actividades

Se introduce

• El signo del parámetro k, positivo si las cargas son del mismo signo y negativo si son de signo contrario, en el contrro titulado Cargas
• La distancia entre las dos cargas para θ=0, en el control titulado Distancia
• La posición angular inicial θ₀ en grados, en el contro titulado Angulo
• Se ha fijado la velocidad angular inical, parte del reposo
• El valor del parámetro, k=1
• La longitud del péndulo, l= 1 m

Se pulsa el botón titulado Nuevo

Referencias

O. Aguilar Loreto, A. Muñoz, A. Jiménez Pérez. Dynamics for an electric pendulum. Revista Mexicana de Física E 65 (2019) 213–217