Carga inducida en un conductor plano
Carga situada a una distancia de una placa conductora
El caso más sencillo es el de una carga q situada a una distancia d de una placa conductora conectada a Tierra. La placa puede reemplazarse por una carga imagen -q, tal como se muestra en la figura.
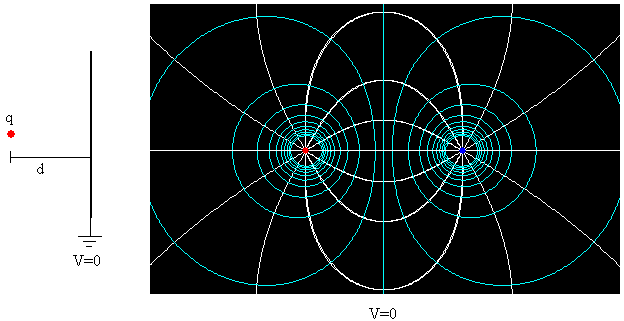
El plano que corta perpendicularmente a la línea que une las dos cargas y que está a la misma distancia de ambas, está a un potencial cero. La parte derecha de la figura, se ha obtenido con el primer programa interactivo de la página titulada "El campo eléctrico de un sistema de dos cargas"
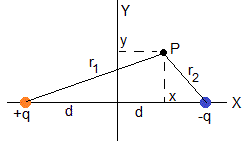
Consideremos el sistema de cargas de la figura, formada por dos cargas +q y -q separadas una distancia 2d. El potencial en el punto P de coordenadas (x,y) producido por las dos cargas es
Por simetría, el potencial en el eje Y y en cualquier punto del plano perpendicular a la línea que une ambas cargas que contiene a dicho eje, es cero.
El campo eléctrico en las proximidades de dicho plano conductor es perpendicular al plano, (tiene la dirección del eje X) tal como se ve en las líneas de fuerza de color blanco de la figura.
Carga inducida en el plano conductor
En los puntos del plano conductor, x=0.
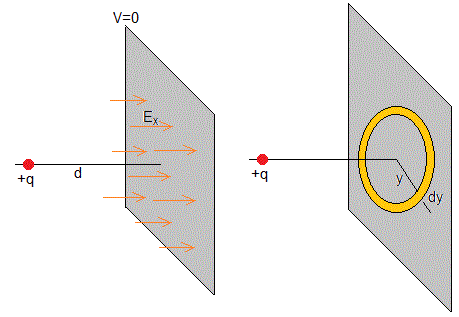
El campo eléctrico en las proximidades de un conductor, tiene por módulo Ex=σ/ε0. Donde σ es la densidad de de carga. Como el sentido del campo eléctrico es hacia el conductor, la densidad de carga σ es negativa σ=-Ex·ε0
f=@(x) 1./(1+x.^2).^(3/2);
fplot(f,[0,5])
grid on
xlabel('y/d')
ylabel('\sigma')
title('Densidad de carga')
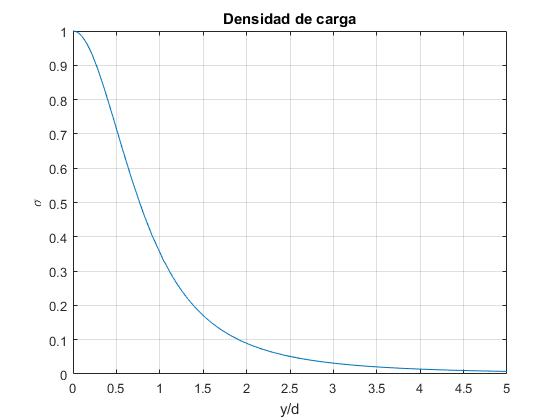
La distribución de carga inducida en el plano conductor tiene simetría cilíndrica alrededor del eje perpendicular al plano y que pasa por la carga. La carga dq inducida en al anillo de radio y, de anchura dy es dq=σ·2πy·dy (figura de la derecha). La carga total inducida en el plano conductor se calcula integrando respecto de y entre 0 e ∞
La carga inducida en el plano conductor es tanto mayor cuanto mayor sea la intensidad del campo eléctrico Ex, en el origen y va disminuyendo a medida que nos alejamos radialmente a lo largo del plano
Movimiento de la carga hacia el plano conductor
La carga q es atraída hacia el plano conductor conectado a tierra, que es lo mismo que decir, que la carga q y su imagen -q se atraen
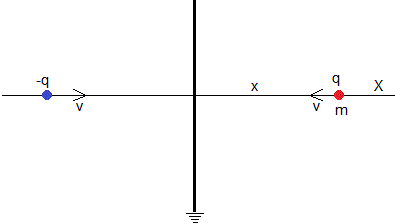
La partícula de masa m y carga +q se suelta a una distancia d del plano conductor. Vamos a calcular el tiempo que tarda en alcanzar la plano conductor conectado a Tierra, x=0
La energía inicial del sistema de dos cargas es
Cuando la partícula se encuentra a una distancia x>0 del plano conductor su velocidad es v=dx/dt<0
Como la energía E es constante, despejamos la velocidad de la partícula
Cuando x tiende a cero, la partícula choca con el plano conductor, la velocidad de la partícula tiende a infinito, lo que no es físicamente correcto
Integrando de nuevo
Hacemos el cambio de variable
El resultado es
La partícula alcanza el plano conductor x=0, en el instante τ
El tiempo t se expresa en función de la distancia x de la partícula cargada al plano conductor
Representamos t/τ en función de x/d
f=@(x) 1-2*asin(sqrt(x))/pi+2*sqrt(x).*sqrt(1-x)/pi;
fplot(f,[0,1])
grid on
xlabel('x/d')
ylabel('t/\tau')
title('Tiempo')
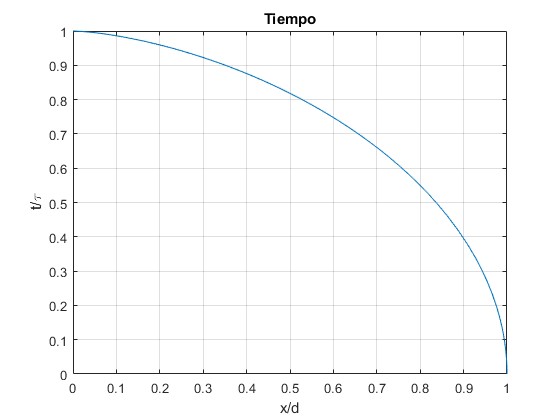
El tiempo que tarda la partícula cargada en chocar con la placa conductora x=0, es
Péndulo frente a un plano conductor
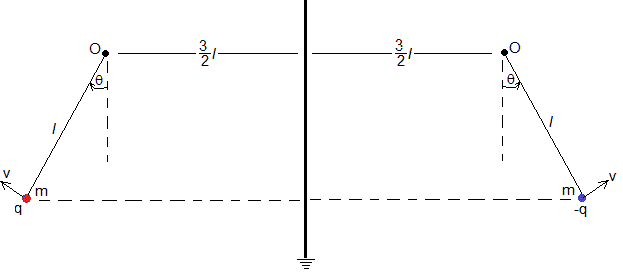
Consideremos un péndulo simple, una partícula de masa m y carga q unida a un hilo inextensible y de masa despreciable de longitud l. El centro de oscilación O está situado a una distancia de 3l/2 de una placa plana conductora conectada a tierra.
En la figura, se muestra la carga imagen -q, situada a una distancia lsinθ+3l/2 de la placa conductora
Energía
La energía del sistema formado por dos cargas eléctricas q y su imagen -q, es la suma de
- La energía cinética de las dos partículas que se mueven con la misma velocidad v
- La energía potencial gravitatoria, tomamos el nivel cero en el punto de suspensión O
- La energía potencial de interacción electrostática
Caso particular
Soltamos el péndulo cuando hace un ángulo θ=30° con la dirección vertical. Calculamos la carga q que deberá llevar para que la posición final del péndulo sea θ=-π/2.
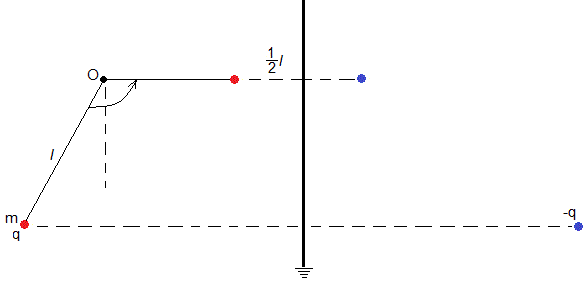
Aplicamos el principio de conservación de la energía. En la situación inicial y en la final la velocidad del péndulo es nula.
Despejamos la carga q y la denominamos qc
Ecuación del movimiento
Las fuerzas sobre la partícula son
El peso, mg
La fuerza de atracción entre las cargas real e imagen
La tensión de la cuerda, T
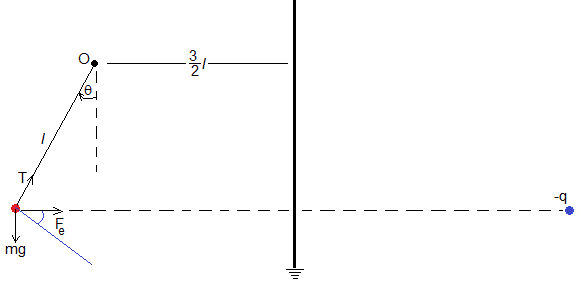
La ecuación del movimiento de la partícula cargada en la dirección tangencial es
Resolvemos la ecuación del movimiento por el procedimiento numérico
La longitud del péndulo l=1 m, y su carga es qc. Representamos la posición θ en función del tiempo t durante varios periodos
L=1; %longitud del péndulo
Q=1; %relación cargas
fg=@(t,x)[x(2); -9.8*(sin(x(1))+Q^2*cos(x(1))/(sqrt(3)*(sin(x(1))+3/2)^2))/L];
[t,x]=ode45(fg,[0,10],[pi/6,0]);
plot(t,x(:,1))
set(gca,'YTick',-pi/2:pi/6:pi/6)
set(gca,'YTickLabel',{'-\pi/2','-\pi/3','-\pi/6','0','\pi/6'})
grid on
xlabel('t')
ylabel('\theta');
title('Péndulo, placa conductora')
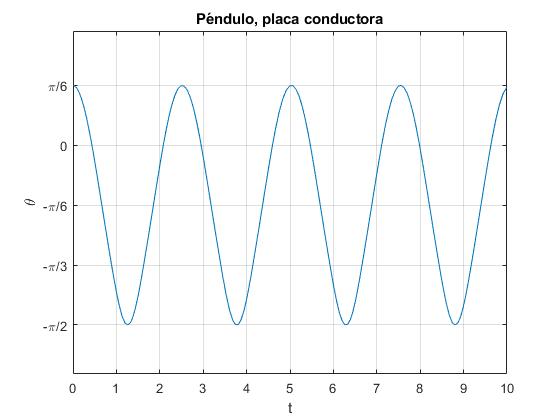
El péndulo se desplaza entre θ=π/6 y θ=-π/2
Como la energía E es constante, derivamos con respecto del tiempo, obteniendo la misma ecuación diferencial
Actividades
Introducimos
- El cociente q/qc, en el control titulado Cociente
- La longitud del péndulo se ha fijado en l=1 m
Observamos el movimiento del péndulo frente a una placa plana conductora conectada a tierra. Se representa la carga imagen -q como un punto de color azul
Se porporcionan los datos del tiempo t, la posición angular θ en grados y la velocidad angular dθ/dt en rad/s
Dipolo eléctrico frente a un plano conductor
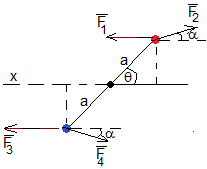
Un dipolo eléctrico (formado por dos cargas +q y -q separadas una distancia 2a) está situado a una distancia x de un plano conductor infinito conectado a tierra. El dipolo hace un ángulo θ con el eje X tal como se muestra en la parte izquierda de la figura
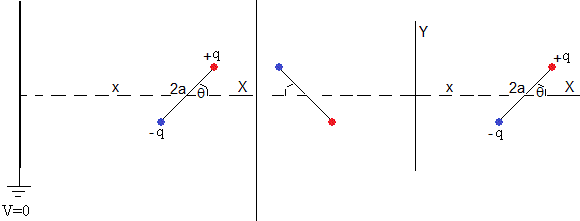
En la parte derecha, se muestra el dipolo y su imagen
Fuerzas
Las fuerzas que ejercen las cargas imagen sobre el dipolo se dibujan en esta figura
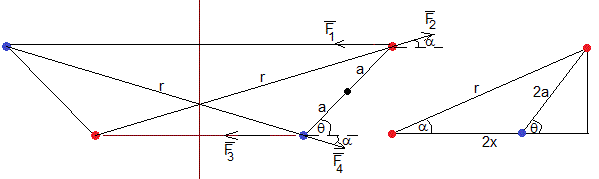
La distancia r entre las cargas real e imagen del mismo signo es
La carga +q experimenta
Una fuerza atractiva de la carga imagen -q, la distancia entre las cargas es 2(x+acosθ)
Una fuerza repulsiva
F 2 →
La carga -q experimenta
Una fuerza atractiva
F 3 → Una fuerza repulsiva
F 4 →
La fuerza eléctrica total sobre el dipolo es
Momentos de las fuerzas
Los momentos de dichas fuerzas respecto del eje del dipolo son
El resultado es
Ecuaciones del movimiento
Escribiremos las ecuaciones del movimiento de en términos de las magnitudes adimensionales, X=x/x0, γ=a/x0 y τ=t/T, siendo x0 la posición inicial del dipolo y T la expresión
Movimiento de traslación del c.m.
Movimiento de rotación alrededor de un eje perpendicular que pasa por el c.m.
Conservación de la energía
La energía electrostática correspondiente a la interacción
- de la carga +q del dipolo con la carga imagen -q, situada a una distancia 2(x+acosθ) y con la carga +q imagen situada a una distancia r
- de la carga -q del dipolo con la carga imagen +q, situada a una distancia 2(x-acosθ) y con la carga -q imagen situada a una distancia r
Cuando el dipolo se encuentra en la posición inicial x0 en reposo,
En el instante t, el dipolo se encuentra en la posición x, su velocidad es dx/dt y gira con velocidad angular dθ/dt
Expresamos la conservación de la energía en términos de las magnitudes adimensionales, X, γ y τ
Ejemplos
Resolvemos numéricamente el sistema de dos ecuaciones diferenciales con las siguientes condiciones iniciales: en el instante τ=0, el dipolo parte de la posición X=1 en reposo, formando un ángulo θ=π/6 (30°) con el eje X, las velocidades dX/dt=0 y dθ/dt=0.
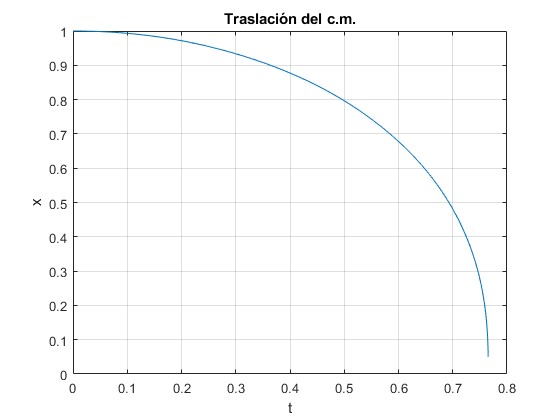
Traslación del centro de masas
function dipolo_imagen
a=0.05; %gamma
th_0=pi/6;
f=@(t,x) [x(2); -(1/(x(1)-a*cos(x(3)))^2-2*x(1)/(x(1)^2+
a^2*sin(x(3))^2)^(3/2)+1/(x(1)+a*cos(x(3)))^2)/(4*a^2); x(4);
sin(2*x(3))*(1/(x(1)^2+a^2*sin(x(3))^2)^(3/2)-
2*x(1)/(x(1)^2-a^2*cos(x(3))^2)^2)/(8*a^2)];
opts=odeset('events',@stop_ode45);
[t,x]=ode45(f,[0,10],[1,0, th_0,0],opts);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('x');
title('Traslación del c.m.')
%energías
U0=1/sqrt(1+a^2*sin(th_0)^2)-1/(1-a^2*cos(th_0)^2);
Ef=a^2*x(:,2).^2+a^4*x(:,4).^2+1./sqrt(x(:,1).^2+a^2*sin(x(:,3)).^2)-
x(:,1)./(x(:,1).^2-a^2*cos(x(:,3)).^2);
disp(U0)
disp(Ef(1:100))
function [value,isterminal,direction]=stop_ode45(~,x)
value=x(1);
isterminal=0;
direction=-1;
end
end
Rotación alrededor de un eje perpendicular que pasa por el centro de masas
Cambiamos las líneas de código
...
plot(t,x(:,3))
grid on
xlabel('t')
ylabel('\theta');
title('Rotación alrededor del c.m.')
...
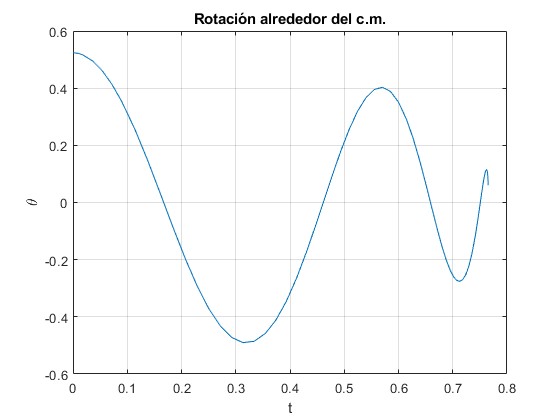
Cuando el dipolo se acerca al plano conductor, las fuerzas son muy intensas y el procedimiento numérico no resuelve bien el sistema de dos ecuaciones diferenciales
Actividades
Se introduce
- El parámetro γ=a/x0 en el contro titulado Brazo
Se pulsa el botón titulado Nuevo
El dipolo parte en reposo de la posición X=1, formando un ángulo θ=π/6 (30°) con el eje X. Se observa el movimiento de traslación del dipolo y su giro alrededor de un eje perpendicular que pasa por el c.m.
En la parte superior, se proporcionan los datos
- Tiempo τ
- Posición, X=x/x0
- Angulo girado, θ
Referencias
Kevin L. Haglin. Point charge dynamics near a grounded conducting plane. Am. J. Phys. 78 (11), November 2010. pp. 1190-1194
Physics Challenge for Teachers and Students. Mirror, mirror... and a ball!. Phys. Teach. 59, 137 (2021); https://doi.org/10.1119/10.0003474
Solution to the February, 2021 Challenge. Mirror, mirror... and the wall!*. Phys. Teach. 59, A303 (2021). https://doi.org/10.1119/10.0004175
J. Pierrus. Solved Problems in Classical Electromagnetism. Analytical and numerical solutions with comments. Oxford University Press (2018). Question 3.28 y 3.29, pp. 173-176.

