Un aerogenerador convierte la energía del viento en energía mecánica que es transformada en energía eléctrica mediante un generador, de un modo similar a las centrales hidráulicas sustituyendo la corriente de agua que circula por una tubería por el viento. La diferencia estriba en que el agua se puede almacenar y canalizar.

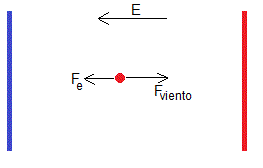
El método EWICON (Electrostatic Wind Energy Converter) se fundamenta en la fuerza que ejerce el viento sobre las partículas cargadas situadas en un campo eléctrico, tal como se aprecia en la figura.

El funcionamiento de un dispositivo EWICON, tal como se aprecia en la figura, es el siguiente:

Se coloca un aislante entre el sistema que produce las partículas cargadas (pulverizador) y tierra. Las partículas cargadas son empujadas por el viento y caen a tierra. La energía potencial del sistema se incrementa y esa energía puede ser aprovechada para realizar un trabajo eléctrico, por ejemplo para mover un motor u otro dispositivo, representado por la resistencia R.

Las partículas cargadas

Las partículas cargadas son gotas de líquido producidas por un pulverizador. Sin embargo, una gota de líquido no puede transportar una carga cualesquiera. En la página titulada Inestabilidad de las gotas de líquido cargadas' se explica la máxima carga que puede acumular una gota de líquido de diametro d, el denominado límite de Rayleigh.

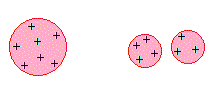
Como consecuencia de la evaporación, el radio de una gota disminuye y se rompe en dos o más gotas cuando llega al límite tal como se muestra en la figura. El proceso de evaporación continua disminuyendo el radio de las gotas y éstas se vuelven a romper cuando se alcanza un nuevo límite.

La evaporación se incrementa con la diferencia de velocidades entre la gota y el aire que le rodea. Cuando la gota se crea, esa diferencia de velocidades es grande y va disminuyendo a medida que la gota se mueve arrastrada por el aire hacia tierra. Otro factor a tener en cuenta, es la humedad del aire.

Fuerzas sobre las partículas cargadas

Las fuerzas que actúan sobre una gota son:

• El peso, m_i es la masa de la gota y g la aceleración de la gravedad

${\displaystyle \overrightarrow{F_g}=-m_{i}g\widehat{k}}$

• La fuerza de empuje que experimenta un cuerpo sumergido en un fluido, donde ρ_a es la densidad del aire, V_i es el volumen de la gota

${\displaystyle \overrightarrow{F_b}={\rho }_{a}g{V}_i\widehat{k}}$

• La fuerza de rozamiento, proporcional a la velocidad relativa de la gota $\overrightarrow{v_i}$ respecto del viento $\overrightarrow{v_i}$, donde η_a es la viscosidad del aire y d_i es el diámetro de la gota

${\displaystyle \overrightarrow{F_r}=3\pi {\eta }_a{d}_i\left(\overrightarrow{v_w}-\overrightarrow{v_i}\right)}$

Esta fórmula es válida siempre que se mantenga el régimen laminar, es decir, que el número de Reynolds sea menor que la unidad

${\displaystyle R_e=\frac{{\rho }_a{d}_i|\overrightarrow{v_w}-\overrightarrow{v_i}|}{{\eta }_a}<1}$

• La fuerza que ejerce el campo eléctrico $\overrightarrow{E}$ , donde q_i es la carga que transporta la gota

${\displaystyle \overrightarrow{F_e}=q_i\overrightarrow{E}}$

El campo eléctrico producido por el dispositivo que crea las gotas cargadas decrece en proporción inversa al cuadrado de la distancia en la dirección del viento 1/r² y tiene sentido contrario a esta velocidad.

• La fuerza de repulsión entre las gotas o bien, la fuerza que ejerce el campo creado por las N-1 gotas sobre una determinada, donde q_i es la carga de la gota considerada

${\displaystyle \overrightarrow{F_i}=\frac{1}{4\pi {\epsilon }_0}{\displaystyle \sum }_{\begin{array}{l}j=1\hfill \\ j\ne i\hfill \end{array}}^N\frac{q_i{q}_j}{r_{ij}^2}{\widehat{r}}_{ij}}$

Ecuación del movimiento de una gota

La segunda ley de Newton se escribe para una gota de diámetro d_i masa m_i, volumen V_i, carga q_i, velocidad $\overrightarrow{v_i}$

${\displaystyle m_i\frac{d^2\overrightarrow{r}}{d{t}^2}=-m_{i}g\widehat{k}+{\rho }_{a}g{V}_i\widehat{k}+3\pi {\eta }_a{d}_i(\overrightarrow{v_w}-\overrightarrow{v_i})+q_i\overrightarrow{E}+\frac{1}{4\pi {\epsilon }_0}{\displaystyle \sum }_{\begin{array}{l}j=1\hfill \\ j\ne i\hfill \end{array}}^N\frac{q_i{q}_j}{r_{ij}^2}{\widehat{r}}_{ij}}$

La energía aprovechable depende de la velocidad del viento, el número de gotas, la cantidad de carga que puede transportar cada una de las gotas y otros factores que precisan de un análisis detallado

Movimiento de una partícula cargada bajo la acción del viento y de un campo eléctrico

En la página titulada Efecto del viento en el movimiento del proyectil, se examina el efecto del viento en el movimiento de un proyectil disparado con un cierto ángulo θ₀. Observamos que al cabo de cierto tiempo, la componente horizontal de la velocidad del proyectil v_x se aproxima a la velocidad del viento u·cos(α), siendo α el ángulo que hace el viento con la horizontal.

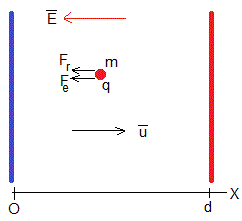
En esta sección, vamos a estudiar el movimiento horizontal de una gota de masa m cargada con una carga q entre las placas de un condensador, empujada por una corriente de aire horizontal, tal como se aprecia en la figura.

Las fuerzas que actúan sobre la gota son:

• la fuerza que ejerce el campo eléctrico sobre la carga q, F_e=q·E
• La fuerza de rozamiento proporcional a la velocidad relativa v-u de la gota v respecto del viento u

La ecuación del movimiento es

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=-qE-bm\left(v-u\right)\\ \frac{dv}{dt}=-\frac{qE}{m}-b\left(v-u\right)\end{array}}$

Se integra esta ecuación diferencial con las siguientes condiciones iniciales: en el instante t=0, v=v₀. Donde, v₀ es la velocidad con la que sale la gota del origen O

${\displaystyle v=\left(u-\frac{qE}{mb}\right)+\left(v_0-u+\frac{qE}{mb}\right)\exp \left(-bt\right)}$

Al cabo de un cierto tiempo, teóricamente infinito, la velocidad alcanza un valor límite constante v_∞, independiente de la velocidad inicial v₀

${\displaystyle v_{\infty }=u-\frac{qE}{mb}}$

Integramos de nuevo, para obtener la posición x de la gota en función del tiempo t

${\displaystyle \begin{array}{l}x={\displaystyle \underset{0}{\overset{t}{\int }}v·dt}={\displaystyle \underset{0}{\overset{t}{\int }}\left(\left(u-\frac{qE}{mb}\right)+\left(v_0-u+\frac{qE}{mb}\right)\exp \left(-bt\right)\right)dt=}\\ \left(u-\frac{qE}{mb}\right)t+\frac{1}{b}\left(v_0-u+\frac{qE}{mb}\right)\left(1-\exp \left(-bt\right)\right)\end{array}}$

b=1; %rozamiento proporcional a la velocidad
k=1; %factor carga (de 0.5 a 2)
% campo que produce una gota, área de las placas S=1 m2
campo=k*5e-10*4*pi*9e9; 
q_m=0.001*k;  %carga dividido masa, masa constante la carga se puede variar
v0=6; %velocidad inicial de la gota
u=3; %velocidad constante del viento
nGotas=5; %número de gota

d=10; %distancia entre placas
x=@(t) (u-q_m*nGotas*campo/b)*t+(v0-u+q_m*nGotas*campo/b)*
(1-exp(-b*t))/b-d;
tt=fzero(x,10); %tiempo que tarda en llegar a la otra placa
%representa la velocidad en función del tiempo
v=@(t) u-q_m*nGotas*campo/b+(v0-u+q_m*nGotas*campo/b)*exp(-b*t);
fplot(v,[0,tt]);
grid on
xlabel('t')
ylabel('v')
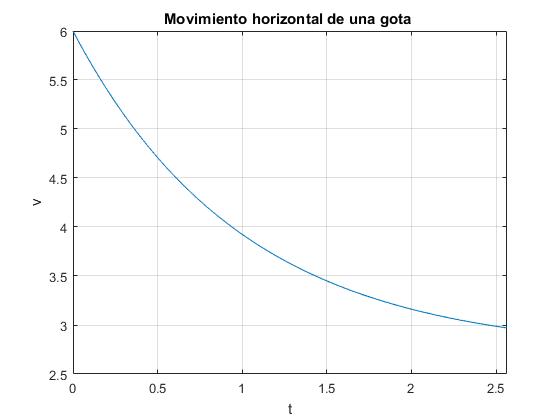
title('Movimiento horizontal de una gota ')

Actividades

Se introduce:

• Un factor k que multiplica a la carga de la gota, de modo que podemos probar gotas con mayor o menor carga q, manteniendo la masa m constante, en el control titulado Carga.
• La velocidad inicial v₀ con la que se lanza la gota en la placa izquierda, en el control titulado Velocidad inicial gota.
• La velocidad del viento u en el control titulado Velocidad viento.
• El valor del parámetro b, el control titulado Parámetro b

Se pulsa el botón titulado Nuevo

La primera gota de masa m toma una carga positiva q de la placa izquierda y se lanza hacia la derecha con velocidad inicial v₀. La placa izquierda se carga negativamente, estableciéndose un campo eléctrico entre las dos placas. El campo eléctrico E ejerce una fuerza sobre la gota en el mismo sentido que el campo. El viento cuya velocidad constante es u empuja la gota hacia la derecha. Cuando la gota llega a la placa derecha le transfiere su carga q y se carga positivamente.

Cuando la primera gota ha llegado a la placa opuesta, sale la segunda que transporta la misma carga q. La diferencia entre la primera y segunda gota, es que la segunda se mueve en un campo eléctrico uniforme E que es el dobe que la primera.

El campo eléctrico es proporcional a la carga de las placas E=nq/(S·ε₀). Donde n es el número de gotas, q es la carga de cada gota y S es el área de las placas. La fuerza de frenado que ejerce el campo eléctrico sobre las gotas es cada vez mayor y eventualemnte, puede deternerlas e incluso hacer que regresen a la placa izquierda de partida

La flecha roja indica la magnitud y dirección del campo eléctrico y la flecha azul señala la velocidad constante del viento.

El programa se detiene cuando el número de gotas n se hace igual a 20 o bien, cuando la velocidad de la gota se hace negativa y ya no avanza hacia la placa derecha

La intensidad del color de las placas es proporcional a la carga de la placa.

En la parte inferior, se representa la velocidad v de la gota en función del tiempo. De este modo el lector puede apreciar el efecto del campo eléctrico, cuando la gota alcanza el valor límite constante v_∞. Una línea horizontal marca la velocidad constante u del viento

Se aconseja probar el caso particular de v₀=0, las gotas parten de la placa izquierda en reposo

Referencias

Dhiradj Djairam. The Electrostatic Wind Energy Converter, electrical performance of a high voltage prototype. Proefschrift. Technische Universiteit Delft (2008)