El condensador plano-paralelo
Se denomina condensador al dispositivo formado por dos conductores cuyas cargas son iguales pero de signo opuesto.
La capacidad C de un condensador se define como el cociente entre la carga Q y la diferencia de potencia V-V’ existente entre ellos.
La unidad de capacidad es el farad o faradio F, aunque se suelen emplear submúltiplos de esta unidad como el microfaradio µF=10-6 F, y el picofaradio, pF=10-12 F.
Un condensador acumula una energía U en forma de campo eléctrico. La fórmula como demostraremos más abajo es
Agrupación de condensadores
La agrupación de varios condensadores de capacidades C1, C2, ... Cn es equivalente a un solo condensador de capacidad Ce. Consideramos la agrupación de tres condensadores de capacidades C1, C2 y C3.
Condensadores en serie
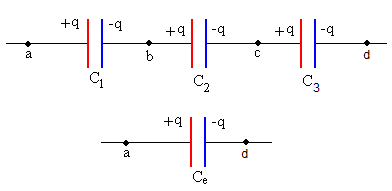
Los condensadores agrupados en serie tienen la misma carga q. La diferencia de potencial entre los extremos a del primer condensador y d del tercero es Vad=Vab+Vbc+Vcd.
Por otra parte, Vad es la diferencia de potencial del condensador equivalente de capacidad Ce.
Simplificando q, obtenemos la fórmula de la capacidad del condensador equivalente Ce conocida las capacidades C1, C2, ... Cn de varios condensadores agrupados en serie
Condensadores en paralelo
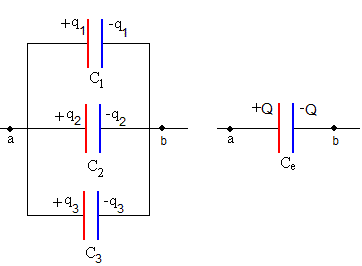
Los condensadores agrupados en paralelo tienen la misma diferencia de potencial Vab entre sus extremos, pero la carga de cada condensador es diferente. La carga del condensador equivalente es igual a la suma de las cargas de los condensadores agrupados en paralelo.
Q=q1+q2+q3
Simplificando Vab, obtenemos la fórmula de la capacidad del condensador equivalente Ce conocida las capacidades C1, C2, ... Cn de varios condensadores agrupados en paralelo
Ejemplo 1
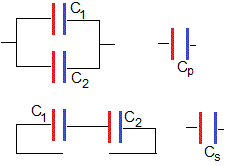
- Agrupamos dos condensadores de capacidad C1 y C2 en paralelo, su capacidad equivalente es Cp
- Agrupamos estos dos condensadores en serie, su capacidad equivalente es Cs.
Calcula las capacidades de los dos condensadores
Ejemplo, sea Cs=2 µF, y Cp=9 µF. Las dos soluciones equivalentes son:
- C2=6 µF y C1=3 µF
- C2=3 µF y C1=6 µF
Ejemplo 2
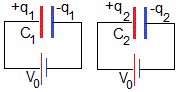
Dos condensadores de capacidades C1 y C1 se cargan inicialmente conectándolos con una batería de V0 voltios. Cada uno de los condensadores adquiere una carga q1=C1·V0 y q2=C2·V0
Se conecta la placa positiva del primer condensador a la placa positiva del segundo. Tendremos dos condensadores en paralelo, cuya capacidad equivalente es C1+C2 y cuya carga es q1+q2.

La diferencia de potencial es
Supongamos que se conecta la placa positiva del primero a la negativa del segundo

La diferencia de potencial es
Ejemplo 3
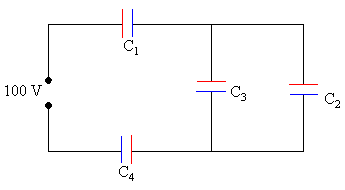
En la figura se representan cuatro condensadores de capacidades C1=0.43·10-9, C2=10-9, C3=1.30·10-9, C4=2.17·10-9 F. Calcular:
- La capacidad del condensador equivalente
- La diferencia de potencial entre las armaduras de cada uno de los condensadores
- La carga de cada condensador
- La capacidad equivalente
- La energía del conjunto
Los condensadores C2 y C3 están en paralelo
C23=C2+C3=2.30·10-9 F
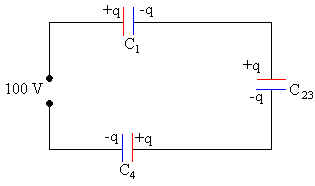
Los condensadores C1, C23 y C4 están en serie
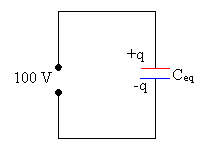
Carga del condensador equivalente y energía almacenada en el mismo
Carga de cada condensador y diferencia de potencial entre sus armaduras
q1=q, V1=q/C1=72.2 V
q4=q, V4=q/C4=14.3 V
V23=q/C23=13.5 V
V2=V23=13.5 V
V3=V23=13.5 V
q2=C2·V2=1.35·10-8 C
q3=C3·V3=1.75·10-8 C
Condensador plano-paralelo
En primer lugar, calculamos el campo creado por una placa plana indefinida, cargada con una densidad de carga σ, aplicando la ley de Gauss.
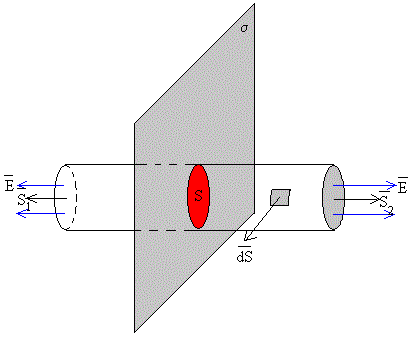
Para una placa indefinida cargada, la aplicación del teorema de Gauss requiere los siguientes pasos:
A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.
Elegir una superficie cerrada apropiada para calcular el flujo
Flujo a través de las bases del cilindro: el campo y el vector superficie son paralelos.
Flujo a través de la superficie lateral del cilindro. El campo es perpendicular al vector superficie , el flujo es cero.
Determinar la carga que hay en el interior de la superficie cerrada
Aplicar el teorema de Gauss y despejar el módulo del campo eléctrico
La dirección del campo es perpendicular a la placa cargada, hacia afuera si la carga es positiva y hacia la placa si la carga es negativa.
Tomamos como superficie cerrada, un cilindro de base S, cuya generatriz es perpendicular a la placa cargada. El flujo tiene dos contribuciones
El flujo total es por tanto; 2ES
La carga (en la figura de color rojo) en el interior de la superficie cerrada vale q=σS, donde σ es la carga por unidad de superficie
El campo producido por una placa infinitamente grande es constante, su dirección es perpendicular a la placa. Esta fórmula es válida para distancias próximas a una placa en comparación con sus dimensiones.
Campo creado por dos placas planas cargadas con cargas iguales y opuestas.
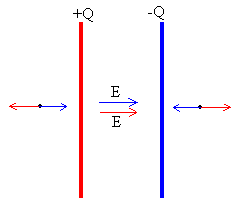
Supondremos que las placas son infinitamente grandes o bien, que la separación entre las placas es pequeña comparada con sus dimensiones.
En la figura, se muestra el campo producido por cada una de las placas y en la figura situda en el centro, el campo resultante. En la figura de la derecha, la representación gráfica del campo en función de x, distancia a la primera placa.
Sea un condensador formado por dos placas iguales de área S, separadas una distancia d, pequeña en comparación con las dimensiones de las placas. El campo se cancela en la región del espacio situado fuera de las placas y se suma en el espacio situado entre las placas. Por tanto, solamente existe campo entre las placas del condensador, siendo despreciable fuera de las mismas.
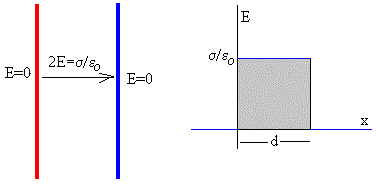
Como el campo es constante, la diferencia de potencial entre las placas se calcula multiplicando el módulo del campo por la separación entre las mismas. El área del rectángulo de la figura.
La capacidad del condensador plano-paralelo será
donde Q=σS es la carga total de la placa del condensador.
La capacidad del condensador solamente depende de su geometría, es decir, del área de las placas S y de la separación entre las mismas d.
Energía de un condensador cargado
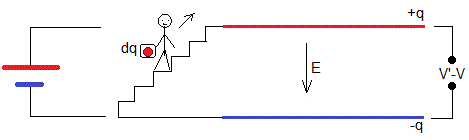
Durante el proceso de carga la batería realiza un trabajo tomado una carga dq de la placa negativa y llevándola a la carga positiva, tal como se muestra en la figura.
Partimos del condensador descargado. Tomamos una carga +dq de la placa inferior y la llevamos a la placa superior. La placa inferior queda cargada con una carga -dq y la superior con una carga +dq. Repetimos el proceso, muchas veces creando un campo eléctrico E entre las placas del condensador.
En un momento dado, la placa superior está cargada con +q y la inferior con -q y la diferencia de potencial entre las mismas será V'-V=q/C
Tomamos otra porción de carga dq de la placa inferior y la llevamos a la placa superior, el trabajo que tenemos que realizar es dW=(V'-V)·dq. Al finalizar el proceso, la carga final de ambas placas es +Q y -Q. El trabajo final realizado es
Para un condensador plano paralelo de área S y separación d, Q=σS, C=ε0S/d. La energía U almacenada en el condensador en forma de campo eléctrico es
El término entre paréntesis es la densidad de energía (energía por unidad de volumen) asociada al campo eléctrico
Condensador plano, no paralelo
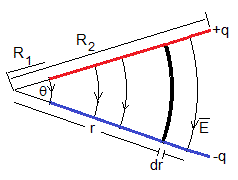
Sea un condensador plano, cuyas placas miden l y R2-R1, no paralelo, las placas forman un ángulo θ tal como se muestra en la figura.
Tomemos una porción de condensador de longitud dr, (en color negro en la figura) su capacidad es
La capacidad del condensador es la suma
La carga de condensador es
Si V'-V es la diferencia de potencial entre las placas. El campo eléctrico es
Su dirección es tangente al arco de radio r
La energía del condensador es
Otra forma de calcular la energía U
V es el volumen del condensador
Referencias
LI Jian—qing,MA Zheng—zheng,TIAN Xu. Discussion on methods of two kinds for calculating capacitance and electric field of an unparallel-plate capacitor. College Physics. 20 August 2008 Volume 27 Issue 8

