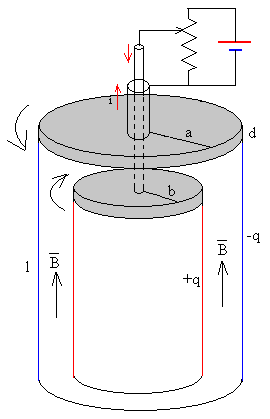
El sistema se muestra en la figura y consiste esencialmente en dos conductores cilíndricos coaxiales de radios a y b, (a>b) y de longitud l, que está en una región en la que existe un campo magnético uniforme $\overrightarrow{B}$ paralelo al eje de los cilindros. Dos placas circulares conductoras de radios a y b y de espesor d, conectan cada cilindro a un cable coaxial.

Inicialmente los conductores cilíndricos están descargados y en reposo, el momento angular inicial es cero. Se conectan a una batería situada en el exterior tal como se indica en la figura. La carga va aumentando poco a poco, hasta que al cabo de un cierto tiempo (teóricamente infinito) los conductores cilíndricos adquieren cargas iguales opuestas -Q y +Q respectivamente.

Momento angular mecánico

En el instante t, la intensidad que circula por los cables coaxiales es i(t).

El campo magnético ejerce una fuerza sobre las corrientes radiales que fluyen desde el borde de las placas circulares hacia los cables coaxiales en la placa superior, y a la inversa en la inferior.

La fuerza que ejerce un campo magnético $\overrightarrow{B}$ sobre una porción de corriente por la que circula una intensidad i es

${\displaystyle \overrightarrow{F}=i{{\displaystyle \int }}^{\text{}}({\widehat{u}}_t\times \overrightarrow{B})dl}$

El vector densidad de corriente $\overrightarrow{J}$ tiene la dirección y sentido del vector unitario ${\widehat{u}}_t$ se define como

${\displaystyle i=\underset{S}{{\displaystyle \int }}\overrightarrow{J}\cdot \overrightarrow{dS}}$

Expresamos la fuerza que ejerce el campo magnético sobre la corriente de intensidad i, en términos del vector densidad de corriente $\overrightarrow{J}$

${\displaystyle \overrightarrow{F_m}={{\displaystyle \int }}^{\text{}}(\overrightarrow{J}\times \overrightarrow{B})dV}$

y el momento de dicha fuerza respecto del eje de rotación

${\displaystyle \overrightarrow{M}={{\displaystyle \int }}^{\text{}}\overrightarrow{r}\times (\overrightarrow{J}\times \overrightarrow{B})dV}$

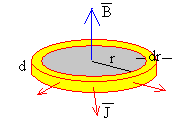
La corriente i que entra en la placa circular inferior atraviesa áreas concéntricas de radio r cada vez mayores. El vector densidad de corriente J=i/(2πrd), tiene dirección radial y sentido hacia fuera en la placa circular inferior, y hacia el centro en la placa circular superior.

Las figuras indican la dirección y el sentido del momento $\overrightarrow{M}$ para la placa circular inferior. Para la placa circular superior el sentido de $\overrightarrow{M}$ es el contrario.

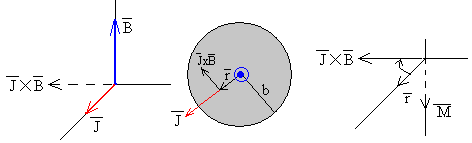
Teniendo en cuenta que el volumen de la capa cilíndrica (en color amarillo) de espesor d comprendida entre r y r+dr es dV=2πrdr·d. El momento M_b de las fuerzas que ejerce el campo magnético sobre la corriente i en la placa inferior es

${\displaystyle M_b=-{\displaystyle \underset{0}{\overset{b}{\int }}r·\frac{i}{2\pi rd}B·2\pi rd·dr}=-iB\frac{b^2}{2}}$

Para la placa circular superior el momento M_a se calcula de forma similar dando

${\displaystyle M_a=iB\frac{a^2}{2}}$

El momento total es M=M_a-M_b=iB(a²-b²)/2.

La dirección de $\overrightarrow{M}$ es la del eje de rotación y su sentido positivo (hacia arriba)

El momento mecánico angular final es

${\displaystyle L_{mec}={\displaystyle \underset{0}{\overset{\infty }{\int }}Mdt}=B\frac{a^2-b^2}{2}{\displaystyle \underset{0}{\overset{\infty }{\int }}i·dt}=B\frac{a^2-b^2}{2}Q}$

donde Q es la carga final de los conductores (véase carga de un condensador)

Como a>b el momento angular mecánico tiene la dirección del eje de rotación y sentido positivo (hacia arriba).

Momento angular del campo electromagnético

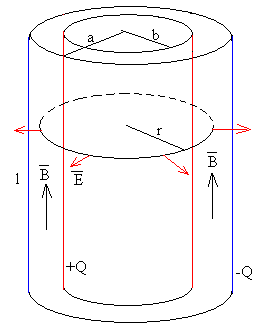
Hemos calculado, aplicando la ley de Gauss, el campo eléctrico producido por dos conductores cilíndricos coaxiales de longitud l y de radios b y a cargados con carga Q iguales y opuestas.

• r<b el campo E=0

• r>a el campo E=0

• b<r<a el campo E=Q/(2πrlε₀)

En la región comprendida entre los dos conductores cilíndricos hay dos campos

• El campo eléctrico que tiene dirección radial y perpendicular al eje del cilindro
• Un campo magnético uniforme paralelo al eje de los cilindros

El módulo del vector de Poynting $\overrightarrow{S}=(\overrightarrow{E}\times \overrightarrow{B})/{\mu }_0$ vale

${\displaystyle S=\frac{1}{{\mu }_0}\frac{Q}{2\pi rl{\epsilon }_0}B}$

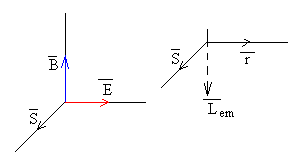
En la figura, se señala la dirección y el sentido del vector $\overrightarrow{S}$.

El momento angular electromagnético es

${\displaystyle \overrightarrow{L_{em}}=\frac{1}{c^2}\underset{V}{{\displaystyle \int }}(\overrightarrow{r}\times \overrightarrow{S})dV}$

Teniendo en cuenta que el volumen de integración es el volumen de la capa cilíndrica de longitud l comprendida entre a y b, y que el elemento de volumen dV=2πrl·dr. Recordando que c es la velocidad de la luz en el vacío y 1/c²=ε₀·μ₀

El módulo del momento angular $\overrightarrow{L_{em}}$ es

${\displaystyle L_{em}=-{\epsilon }_0{\mu }_0{\displaystyle \underset{b}{\overset{a}{\int }}r\frac{1}{{\mu }_0}\frac{Q}{2\pi rl{\epsilon }_0}B·2\pi rldr}=-{\displaystyle \underset{b}{\overset{a}{\int }}QBrdr}=-B\frac{a^2-b^2}{2}Q}$

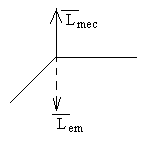
La dirección de $\overrightarrow{L_{cm}}$ es la del eje de rotación y su sentido negativo (hacia abajo).

Hemos comprobado por tanto, el principio de conservación del momento angular

${\displaystyle \overrightarrow{L_{mec}}+\overrightarrow{L_{cm}}=0}$

El momento angular inicial y final del sistema formado por los dos cilindros coaxiales, y sus correspondientes placas circulares y el campo electromagnético es cero.

Referencias

Aguirregabiria J. M., Hernández A. The Feynman paradox revisited.  Eur. J. Phys. 2 (1981), pp. 168-170.

Bahder T, Sak J. Elementary solution to Feynman’s disk paradox. Am. J. Phys. 53 (3) May 1993, pp. 495-497.

Driver H. S. T. Angular momentum in static electric and magnetic fields: A simple case. Am. J. Phys. 55 (8) August 1987. pp. 755-757