Condensador cilíndrico

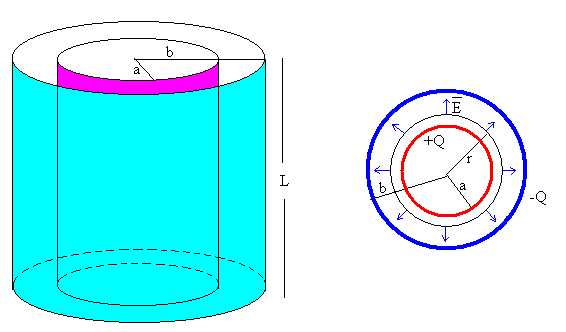
El campo existente entre las armaduras de un condensador cilíndrico de radio interior a, radio exterior b y longitud L, cargado con cargas +Q y –Q, respectivamente, se calcula aplicando la ley de Gauss a la región a<r<b, ya que tanto fuera como dentro del condensador el campo eléctrico es cero.

La aplicación del teorema de Gauss, es similar al de una línea cargada,y  requiere los siguientes pasos:

1. A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.

La dirección del campo es radial y perpendicular al eje del cilindro.

2. Elegir una superficie cerrada apropiada para calcular el flujo

Tomamos como superficie cerrada, un cilindro de radio r y longitud L. Tal como se muestra en la figura. El cálculo del flujo, tiene dos términos:

• Flujo a través de las bases del cilindro: el campo y el vector superficie son perpendiculares, el flujo es cero.
• Flujo a través de la superficie lateral del cilindro. El campo $\overrightarrow{E}$ es paralelo al vector superficie $\overrightarrow{dS}$ y el campo es constante en todos los puntos de la superficie lateral, por lo que,

${\displaystyle \underset{S}{{\displaystyle \int }}\overrightarrow{E}\cdot \overrightarrow{dS}=\underset{S}{{\displaystyle \int }}EdS\cos 0º=E\underset{S}{{\displaystyle \int }}dS=E2\pi rL}$

El flujo total es E·2π rL

3. Determinar la carga que hay en el interior de la superficie cerrada

La carga en el interior de la superficie cerrada vale +Q, que es la carga de la armadura cilíndrica interior

4. Aplicar el teorema de Gauss y despejar el módulo del campo eléctrico

${\displaystyle E2\pi rL=\frac{Q}{{\epsilon }_0}E=\frac{Q}{2\pi {\epsilon }_{0}rL}}$

Ahora, es fácil demostrar, aplicando el teorema de Gauss que el campo en las regiones r<a y r>b es nulo.

• En el primer caso, si tomamos una superficie cilíndrica de radio r<a y de longitud L, dicha superficie no encierra carga alguna.
• En el segundo caso, si tomamos una superficie cilíndrica de radio r>b y longitud L, la carga total encerrada es +Q-Q=0, es nula, el flujo es cero y el campo es cero.

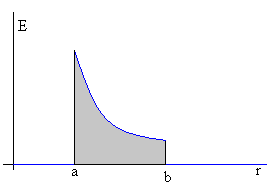
En la figura, se muestra la representación gráfica del campo E en función de la distancia radial r.

La diferencia de potencial entre las placas del condensador se calcula integrando, (área sombreada de la figura).

${\displaystyle V-V\text{'}={\displaystyle \underset{a}{\overset{b}{\int }}E\cdot dr}=\frac{Q}{2\pi {\epsilon }_{0}L}\ln \frac{b}{a}}$

La capacidad es

${\displaystyle C=\frac{Q}{V-V\text{'}}=\frac{2\pi {\epsilon }_{0}L}{\ln (b/a)}}$

La capacidad solamente depende de la geometría del condensador (radio a y radio b de sus armaduras, y longitud L del condensador)

Energía del condensador

${\displaystyle U=\frac{1}{2}C{V}^2}$

Dos superficies cilíndricas equipotenciales

Regresamos a la página titulada Principio de superposición de campos.

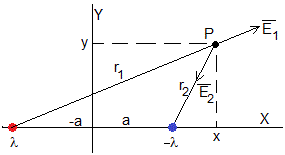
El potencial en un punto P (x, y) producido por dos hilos rectilíneos cargados con cargas iguales y opuestas -λ y +λ C/m, separados 2a, es

${\displaystyle V(x,y)=\frac{\lambda }{2\pi {\epsilon }_0}\ln \left(\frac{r_2}{r_1}\right)=\frac{\lambda }{4\pi {\epsilon }_0}\ln \left(\frac{{\left(x-a\right)}^2+y^2}{{\left(x+a\right)}^2+y^2}\right)}$

Demostramos que las equipotenciales

${\displaystyle V(x,y)=\frac{\lambda }{4\pi {\epsilon }_0}\ln k}$

son superficies cilíndricas de longitud infinita paralelas a los hilos. En el plano XY son circunferencias de ecuación

${\displaystyle {\left(x-\frac{1+k}{1-k}a\right)}^2+y^2=\frac{4k}{{(1-k)}^2}{a}^2}$

cuyo centro y radio son

${\displaystyle \begin{array}{l}\left(\frac{1+k}{1-k}a\mathrm{,0}\right)\\ R^2=\frac{4k}{{(1-k)}^2}{a}^2\end{array}}$

Sustituiremos una equipotencial por un conductor cilíndrico de longitud infinita al mismo potencial.

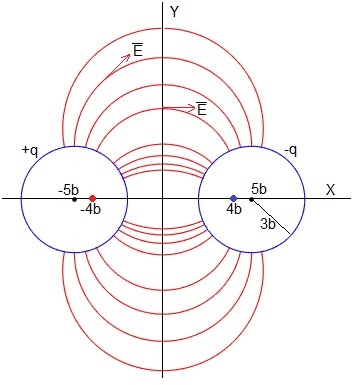
Supongamos dos conductores de radio R=3b y cuyos ejes está situados en (±5b,0). Con estos datos, calculamos la separación 2a ente los hilos rectilíneos cargados y el valor de constante k relacionada con el potencial del conductor

${\displaystyle \begin{array}{l}\frac{1+k}{1-k}a=5b\\ {\left(3b\right)}^2=\frac{4k}{{(1-k)}^2}{a}^2\end{array}}$

Obtenemos la ecuación de segundo grado

${\displaystyle \begin{array}{l}9{\left(1+k\right)}^2=100k\\ k_1=\frac{1}{9},k_2=\mathrm{9,}a=4b\end{array}}$

a=4; % 2a es la distancia entre los dos hilos
hold on
for k=[1:4, -(1:4)] %líneas de fuerza
   R=sqrt(a^2+k^2);
   y1=k;
   fplot(@(t) R*cos(t), @(t) y1+R*sin(t),[0,2*pi],'r')
end
for k=[9, 1/9] %equipotenciales
   R=2*a*sqrt(k)/(1-k);
   x1=(1+k)*a/(1-k);
   fplot(@(t) x1+R*cos(t), @(t) R*sin(t),[0,2*pi],'b')
    plot(x1,0,'ko','markersize',3,'markerfacecolor','k') %centro
end
hold off
axis equal
axis off

• El potencial del cilindro izquierdo (k=9) es

${\displaystyle V_1=\frac{\lambda }{4\pi {\epsilon }_0}\ln 9=\frac{\lambda }{2\pi {\epsilon }_0}\ln 3}$

• El potencial del cilindro derecho (k=1/9) es

${\displaystyle V_2=\frac{\lambda }{4\pi {\epsilon }_0}\ln \frac{1}{9}=-\frac{\lambda }{2\pi {\epsilon }_0}\ln 3}$

La diferencia de potencial

${\displaystyle \Delta V=V_1-V_2=\frac{\lambda }{\pi {\epsilon }_0}\ln 3}$

Si los conductores cilíndricos tienen una longitud l>>R, y están cargados con +q y -q, respectivamente, la diferencia de potencial es

${\displaystyle \Delta V=\frac{q}{\pi {\epsilon }_{0}l}\ln 3}$

La capacidad

${\displaystyle C=\frac{q}{\Delta V}=\frac{\pi {\epsilon }_{0}l}{\ln 3}}$

Intensidad de la corriente eléctrica

El campo eléctrico producido por estos dos conductores cilíndricos en el punto P(x, y), es

${\displaystyle \overrightarrow{E}=\frac{\lambda }{\pi {\epsilon }_0}\frac{a(y^2+a^2-x^2)\widehat{i}-2axy\widehat{j}}{a^4+{\left(x^2+y^2\right)}^2+2a^2(y^2-x^2)}}$

En el interior de cada uno de los conductores cilíndricos, el campo eléctrico es nulo, de acuerdo a la ley de Gauss y el potencial es constante e igual al de la superficie del conductor.

Se han representado algunas líneas de fuerza en color rojo, la dirección del campo eléctrico es tangente en cada punto a las líneas de fuerza

Supongamos que estos condensadores se introducen en un medio conductor de conductividad σ. Los portadores de carga siguen las líneas de fuerza,

${\displaystyle \overrightarrow{J}=\sigma \overrightarrow{E}}$

J es la densidad de corriente, carga por unidad de área y de tiempo

En el plano x=0, las componentes del campo eléctrico son

${\displaystyle \begin{array}{l}{E}_x=\frac{\lambda }{\pi {\epsilon }_0}\frac{a(y^2+a^2)}{a^4+y^4+2a^2{y}^2}=\frac{\lambda }{\pi {\epsilon }_0}\frac{a}{y^2+a^2}=\frac{\Delta V}{\ln 3}\frac{4b}{y^2+{\left(4b\right)}^2}\\ E_y=0\end{array}}$

La intensidad de la corriente es

${\displaystyle \begin{array}{l}i={\displaystyle \int \overrightarrow{J}·\overrightarrow{dS}}={\displaystyle \int \sigma E_x·\left(ldy\right)}\\ =\sigma l{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{\Delta V}{\ln 3}\frac{4b}{y^2+{\left(4b\right)}^2}dy}=\sigma l\frac{\Delta V}{\ln 3}{\arctan \left(\frac{y}{4b}\right)|}_{-\infty }^{\infty }=\sigma l\frac{\Delta V}{\ln 3}\pi \end{array}}$

La resistencia (no confundir con el radio R), es

${\displaystyle R=\frac{\Delta V}{i}=\frac{\ln 3}{\pi \sigma l}}$

Condensador esférico

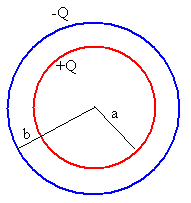
Un condensador esférico está formado por dos superficies conductoras esféricas, concéntricas de radios a y b, cargadas con cargas iguales y opuestas +Q y –Q, respectivamente.

Situamos imaginariamente, una superficie esférica concéntrica de radio r, para determinar el campo eléctrico en las distintas regiones aplicando la ley de Gauss.

En este problema de simetría esférica, el campo eléctrico tiene dirección radial y su módulo es constante en todos los puntos de una superficie esférica de radio r. El flujo del campo eléctrico $\overrightarrow{E}$ a través de dicha superficie cerrada vale

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}={{\displaystyle \oint }}^{\text{}}E·dS·\cos 0º=E{{\displaystyle \oint }}^{\text{}}dS=E·4\pi r^2}$

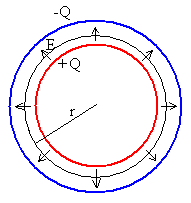
Determinamos la carga q encerrada en dicha superficie esférica, para distintos valores del radio r, aplicamos la ley de Gauss

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\frac{q}{{\epsilon }_0}}$

• Para r<a, la superficie esférica de radio r, no contiene ninguna carga, q=0, y E=0

• Para a<r<b, la superficie esférica de radio r, contiene una carga, q=+Q,

${\displaystyle E·4\pi r^2=\frac{Q}{{\epsilon }_0}E=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r^2}}$

• Para r>b, la superficie esférica de radio r, contiene una carga, q=+Q-Q=0, y E=0

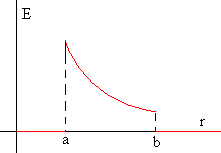
En la figura, se representa el módulo del campo E en función de r.

La diferencia de potencial entre las dos placas es de radios a y b es

${\displaystyle V\text{'}-V={\displaystyle \underset{a}{\overset{b}{\int }}\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r^2}dr=}\frac{1}{4\pi {\epsilon }_0}\left(\frac{1}{a}-\frac{1}{b}\right)}$

La capacidad de un condensador esférico es

${\displaystyle C=\frac{Q}{V\text{'}-V}=\frac{4\pi {\epsilon }_0}{(1/a-1/b)}}$

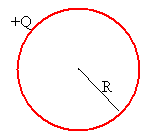
Si el radio del segundo conductor esférico es muy grande b→∞, entonces tenemos la capacidad de un condensador esférico de radio R=a

${\displaystyle C=4\pi {\epsilon }_{0}R}$

Suponiendo que la Tierra es un conductor esférico de radio R=6370 km, su capacidad sería

${\displaystyle C=\frac{6370·{10}^3}{9·{10}^9}=7.08·{10}^{-4}\text{F}}$

Se conectan dos esferas conductoras

Sean dos esferas conductoras de radios R₁ y R₂ respectivamente, que están inicialmente aisladas una de la otra y cargadas con cargas Q₁ y Q₂ respectivamente.

Los potenciales de las superficies de las dos esferas son, respectivamente

${\displaystyle V_1=\frac{1}{4\pi {\epsilon }_0}\frac{Q_1}{R_1}{V}_2=\frac{1}{4\pi {\epsilon }_0}\frac{Q_2}{R_2}}$

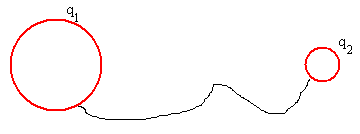
Se ponen en contacto las dos esferas mediante un cable suficientemente largo y fino con el fin de que el campo eléctrico producido por una esfera no perturbe la distribución de cargas en la superficie de la otra. El cable acumulará una carga muy pequeña, y asegurará que el proceso de transferencia de carga sea lento

La carga pasa de una esfera a la otra hasta que sus potenciales se igualan.

${\displaystyle \begin{array}{l}V=\frac{1}{4\pi {\epsilon }_0}\frac{q_1}{R_1}=\frac{1}{4\pi {\epsilon }_0}\frac{q_2}{R_2}\\ Q_1+Q_2=q_1+q_2\end{array}}$

En este sistema de dos ecuaciones con dos incógnitas despejamos q₁ y q₂

${\displaystyle q_1=\frac{R_1}{R_1+R_2}(Q_1+Q_2)q_2=\frac{R_2}{R_1+R_2}(Q_1+Q_2)}$

El potencial común V vale

${\displaystyle V=\frac{Q_1+Q_2}{R_1+R_2}}$

Proceso de carga de una esfera conductora

Un ejemplo significativo de transferencia de carga es el siguiente

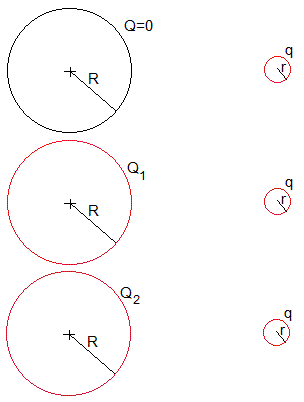
Una esfera conductora de radio R=10 m inicialmente descargada se conecta mediante un cable largo y fino a otra esfera conductora inicialmente cargada q de radio r=1 m. En consecuencia, la esfera grande adquiere una carga Q₁.

La esfera grande inicialmente cargada con Q₁ se vuelve a conectar a otra esfera pequeña idéntica, inicialmente cargada con q. En consecuencia, la esfera grande adquiere una carga Q₂

y así, se repite el proceso n veces

• Se pide calcular Q_n

• Calcular n para que la carga de la esfera grande sea mayor o igual que 9q, Q_n≥9q

El proceso de carga de la esfera grande consta de las siguientes etapas

1. Se conecta la esfera grande descargada con la pequeña esfera con carga q

${\displaystyle \begin{array}{l}\{\begin{array}{l}q=Q_1+q\text{'}\\ \frac{1}{4\pi {\epsilon }_0}\frac{Q_1}{R}=\frac{1}{4\pi {\epsilon }_0}\frac{q\text{'}}{r}\end{array}\\ Q_1=\frac{q}{1+\frac{r}{R}}\end{array}}$

2. Se conecta la esfera grande que ha adquirido una carga Q₁ con la pequeña esfera con carga q

${\displaystyle \begin{array}{l}\{\begin{array}{l}q+Q_1=Q_2+q\text{'}\\ \frac{1}{4\pi {\epsilon }_0}\frac{Q_2}{R}=\frac{1}{4\pi {\epsilon }_0}\frac{q\text{'}}{r}\end{array}\\ Q_2=\frac{q+q\left(1+\frac{r}{R}\right)}{{\left(1+\frac{r}{R}\right)}^2}\end{array}}$

3. Se conecta la esfera grande que ha adquirido una carga Q₂ con la pequeña esfera con carga q

${\displaystyle \begin{array}{l}\{\begin{array}{l}q+Q_2=Q_3+q\text{'}\\ \frac{1}{4\pi {\epsilon }_0}\frac{Q_3}{R}=\frac{1}{4\pi {\epsilon }_0}\frac{q\text{'}}{r}\end{array}\\ Q_3=\frac{q+q\left(1+\frac{r}{R}\right)+q{\left(1+\frac{r}{R}\right)}^2}{{\left(1+\frac{r}{R}\right)}^3}\end{array}}$

4. y así, sucesivamente...

5. Se conecta la esfera grande que ha adquirido una carga Q_n-1 con la pequeña esfera con carga q

${\displaystyle \begin{array}{l}\{\begin{array}{l}q+Q_{n-1}=Q_n+q\text{'}\\ \frac{1}{4\pi {\epsilon }_0}\frac{Q_n}{R}=\frac{1}{4\pi {\epsilon }_0}\frac{q\text{'}}{r}\end{array}\\ Q_n=\frac{q+q\left(1+\frac{r}{R}\right)+q{\left(1+\frac{r}{R}\right)}^2+\mathrm{...}+q{\left(1+\frac{r}{R}\right)}^{n-1}}{{\left(1+\frac{r}{R}\right)}^n}\end{array}}$

El numerador es la suma de n-1 términos de una progresión geométrica de razón 1+r/R

${\displaystyle S_{n-1}=1\frac{1-{\left(1+\frac{r}{R}\right)}^n}{1-\left(1+\frac{r}{R}\right)}=\frac{R}{r}\left({\left(1+\frac{r}{R}\right)}^n-1\right)}$

La carga Q_n vale

${\displaystyle Q_n=q\frac{R}{r}\left(1-\frac{1}{{\left(1+\frac{r}{R}\right)}^n}\right)}$

Con los datos del problema

${\displaystyle Q_n=10q\left(1-{\left(\frac{10}{11}\right)}^n\right)}$

n=1:50;
Q=10*(1-(10/11).^n);
plot(n,Q,'ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('n')
ylabel('Q_n/q')
title('Proceso de carga')



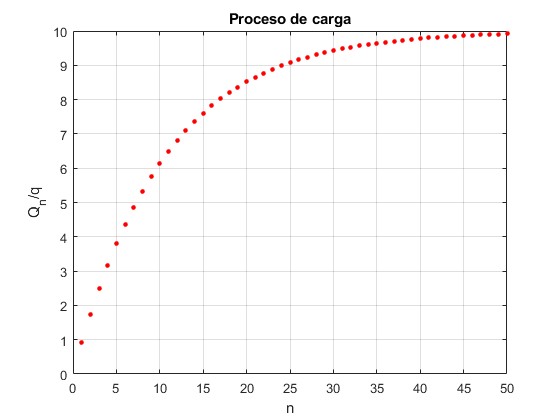
La carga final de la esfera grande tiende a 10q cuando el número de etapas n es grande

Para que Q_n≥9q

${\displaystyle \begin{array}{l}1-{\left(\frac{10}{11}\right)}^n\ge \frac{9q}{10q}\\ 0.1\ge {\left(\frac{10}{11}\right)}^n\\ n\ge \frac{\ln 0.1}{\ln \left(\frac{10}{11}\right)}\\ n\ge 24.16\end{array}}$

El valor de n=25. Comprobación

>> n=24:25;
>> 10*(1-(10/11).^n)
ans =    8.9847    9.0770

Para n=24, Q₂₄=8.9847 y para n=25, Q₂₅=9.0770, algo más que 9q

Gotas que se juntan

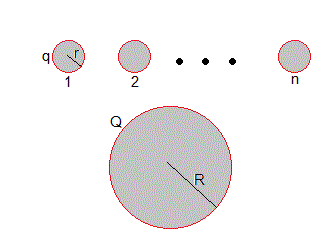
n gotas idénticas de radio r, cargadas con una carga q cada una, se fusionan para producir una gota más grande esférica de radio R y carga Q=nq.

${\displaystyle \frac{4}{3}\pi R^3=n\frac{4}{3}\pi r^{3}R=n^{1/3}r}$

Supondremos que las gotas son conductores (por ejemplo, gotas de mercurio), la capacidad de cada una de las gotas de radio r y de la gota de radio R son, respectivamente

${\displaystyle \begin{array}{l}{C}_r=4\pi {\epsilon }_{0}r\\ C_R=4\pi {\epsilon }_{0}R=4\pi {\epsilon }_0{n}^{1/3}r=n^{1/3}{C}_r\end{array}}$

El potencial de cada una de las gotas de radio r y de la gota de radio R son, respectivamente

${\displaystyle \begin{array}{l}{V}_r=\frac{q}{C_r}\\ V_R=\frac{Q}{C_R}=\frac{nq}{n^{1/3}{C}_r}=n^{2/3}{V}_r\end{array}}$

La energía electrostática de todas las gotas de radio r y de la gota resultante de radio R son, respectivamente

${\displaystyle \begin{array}{l}{U}_r=n\left(\frac{1}{2}\frac{q^2}{C_r}\right)\\ U_R=\frac{1}{2}\frac{Q^2}{C_R}=\frac{1}{2}\frac{{\left(nq\right)}^2}{n^{1/3}{C}_r}=n^{5/3}\left(\frac{1}{2}\frac{q^2}{C_r}\right)\end{array}}$

La energía final es mayor que la inicial, hay que realizar un trabajo para que las gotas se junten

Referencias

Asian Physics Olympiad, 2013 APhO, Theoretical Question 1

Online Physics Olympiad 2020. Problema 15, pp. 14