Fuerza magnética sobre conductor rectilíneo. La balanza de corriente
Intensidad de la corriente
La intensidad de la corriente eléctrica es la carga que atraviesa la sección normal S del conductor en la unidad de tiempo.
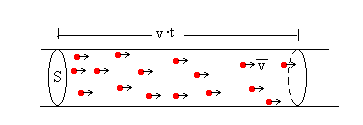
Sea n el número de partículas por unidad de volumen, v la velocidad media de dichas partículas, S la sección del haz y q la carga de cada partícula.
La carga Q que atraviesa la sección normal S en el tiempo t, es la contenida en un cilindro de sección S y longitud v·t.
Carga Q= (número de partículas por unidad de volumen, n)·(carga de cada partícula, q)· (volumen del cilindro, Svt)
Q=n·qS·v·t
Dividiendo Q entre el tiempo t obtenemos la intensidad de la corriente eléctrica.
i=nqvS
La intensidad es el flujo de carga o la carga que atraviesa la sección normal S en la unidad de tiempo, que es el producto de los siguientes términos:
- Número de partículas por unidad de volumen, n
- La carga de cada partícula, q.
- El área de la sección normal, S
- La velocidad media de las partículas, v.
Fuerza sobre una porción de conductor rectilíneo.
En el espectrómetro de masas o en el ciclotrón, ya hemos estudiado la fuerza que ejerce un campo magnético sobre un portador de carga y el movimiento que produce.
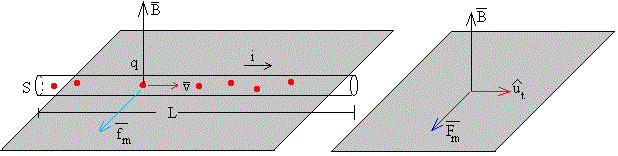
En la figura, se muestra la dirección y sentido de la fuerza que ejerce el campo magnético sobre un portador de carga positivo q, que se mueve hacia la derecha con velocidad .
Calculemos la fuerza sobre todos los portadores (nSL) de carga contenidos en la longitud L del conductor.
El vector unitario tiene la misma dirección y sentido que el vector velocidad o el sentido en el que se mueven los portadores de carga positiva.
En el caso de que el conductor no sea rectilíneo, o el campo magnético no se constante, se ha de calcular la fuerza sobre un elemento de corriente dl
- Las componentes de dicha fuerza dFx y dFy
- Se ha de comprobar si hay simetría de modo que alguna de las componentes sea nula
- Finalmente, se calculará por integración las componentes de la fuerza total
La balanza de corriente
En esta sección, vamos a estudiar cómo funciona una balanza de corriente
Antes de conectar la corriente
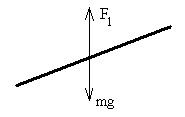
Para que la varilla esté en equilibrio, la fuerza que ejerce el brazo de la balanza F1 deberá ser igual al peso de la varilla
F1=mg
Después de conectar la varilla a la batería
Por la varilla circula una corriente de intensidad i. La fuerza que ejerce el campo magnético es
donde es el campo magnético, L, la longitud del conductor y es un vector que nos indica el sentido de la corriente.
Si el campo y la porción de corriente son perpendiculares, el módulo de la fuerza es
Fm=iLB.
El sentido de la fuerza Fm se muestra en la figura para los distintos casos
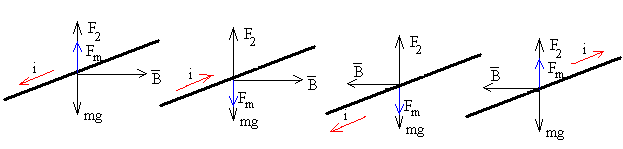
Sobre la varilla en equilibrio actúan las siguientes fuerzas, el peso de la varilla, la fuerza que ejerce el campo magnético y la fuerza F2 que ejerce el brazo de la balanza, para que la varilla esté en equilibrio.
F2+Fm=mg
La fuerza que ejerce el campo magnético sobre la corriente Fm se puede sumar o restar al peso dependiendo de cómo se disponga los polos del imán o del sentido de la corriente en la varilla.
Actividades
El programa interactivo genera un número aleatorio comprendido entre 700 y 900 que representa la masa de la varilla en miligramos.
Para pesar la varilla, movemos con el puntero del ratón los cursores de colores rojo, azul y negro
Ejemplo:
Hemos pesado la varilla resultando F1=862 mg
Se introduce
- la intensidad del campo magnético (en gauss), en el control titulado Campo magnético
- la intensidad de la corriente (en A), en el control titulado Intensidad
Estos valores pueden ser positivos o negativos.
Se pulsa el botón titulado ► y se conecta los extremos de la varilla a los polos de la batería.
Ejemplo:
- Intensidad, i=2.0 A
- Campo magnético, 20.0 gauss, B=0.002 T
- La longitud de la varilla, L=0.2 m, está fijada por el programa
Verificamos que la fuerza que ejerce el campo magnético sobre la corriente rectilínea señalada por una flecha de color azul es hacia arriba. Por tanto, la balanza se desequilibra. Equilibramos la balanza moviendo los cursores a la posición que marca F2=780 mg. Por tanto,
- La fuerza que ejerce el campo magnético es Fm=F1-F2=862-780=82 mg. Multiplicamos el peso en kg por 9.8 para convertir la medida en N, 82·10-6·9.8=8.04·10-4 N
- La fuerza que ejerce el campo magnético es Fm=iBL=2·0.002·0.2=8·10-4 N
Experimentamos con el programa, introduciendo otros valores del campo magnético (positivos o negativos) y de la corriente (positivos o negativos) en los intervalos especificados.
- Comprobar el sentido de la fuerza que ejerce el campo magnético sobre la porción de corriente rectilínea
- Determinar el valor de dicha fuerza mediante la balanza.
Práctica de laboratorio

Sobre la varilla en equilibrio actúan las siguientes fuerzas, el peso de la varilla, la fuerza que ejerce el campo magnético y la fuerza F2 que ejerce la balanza, para que la varilla esté en equilibrio.
F2+Fm=mg
La fuerza que ejerce el campo magnético sobre la corriente Fm se puede sumar o restar al peso dependiendo de cómo se disponga los polos del imán o del sentido de la corriente en la varilla
En el dispositivo experimental de PASCO, el campo magnético producido por los imanes ejerce una fuerza Fm sobre la porción de corriente rectilínea de longitud L. Los imanes están sobre la balanza y la corriente está fija. Por la tercera ley de Newton, la corriente ejerce una fuerza Fm igual y de sentido contrario sobre los imanes y esto se refleja en el indicador de la balanza. La fuerza Fm es la diferencia en gramos entre lo que indica la balanza cuando pasa corriente y cuando no pasa corriente.
Poniendo el imán sobre la balanza y tarando a cero, el indicador de la balanza mide directamente la fuerza Fm que ejerce el campo magnético sobre la porción de corriente rectilínea.
Para convertir la fuerza magnética medida en gramos a Newtons, se ha de multiplicar por el factor 0.0098 N/g
Fuerza en función de la intensidad
| Longitud (cm) | 1.2 |
|---|---|
| Corriente (A) | Fuerza magnética (N) |
| 0 | 0 |
| 0.5 | 3.04·10-3 |
| 1 | 5.39·10-3 |
| 1.5 | 7.74·10-3 |
| 2 | 10.0·10-3 |
x=[0,0.5,1,1.5,2];
>> y=[0,3.04,5.39,7.74,10]/1000;
>> plot(x,y, 'o','markersize',3, 'markeredgecolor','r'
,'markerfacecolor','r')
>> xlabel('i(A)')
>> ylabel('F_m (mN)')
>> title('Fuerza en función de la intensidad')
Aparece la ventana gráfica. En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, marcamos la casilla Show equations.
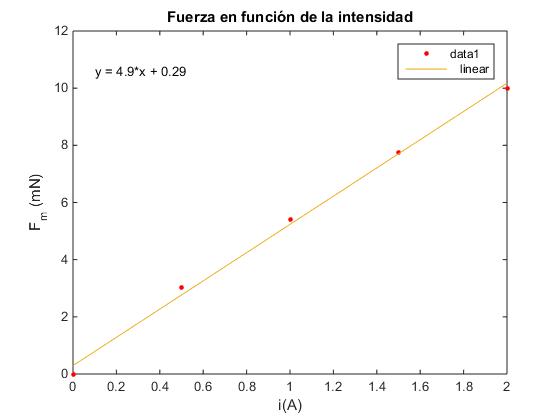
Fuerza en función de la longitud de la corriente
| Intensidad (A) | 1.2 |
|---|---|
| Longitud (cm) | Fuerza magnética (N) |
| 1.2 | 0.98·10-3 |
| 2.2 | 1.37·10-3 |
| 3.2 | 1.76·10-3 |
| 4.2 | 2.06·10-3 |
| 6.4 | 2.65·10-3 |
| 8.4 | 3.43·10-3 |
>>x=[1.2,2.2,3.2,4.2,6.4,8.4];
>> y=[0.98,1.37,1.76,2.06,2.65,3.43];
>> plot(x,y, 'o','markersize',3, 'markeredgecolor','r',
'markerfacecolor','r')
>> xlabel('L(cm)')
>> ylabel('F_m (mN)')
>> title('Fuerza en función de la longitud')
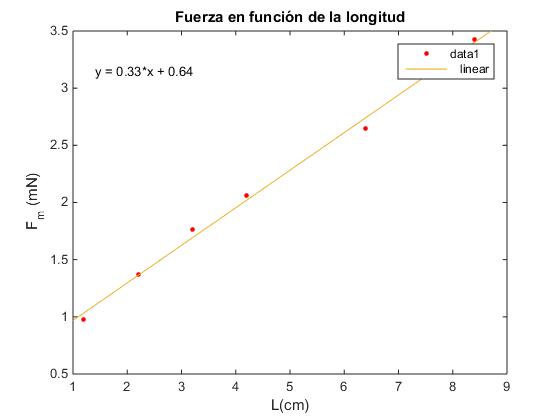
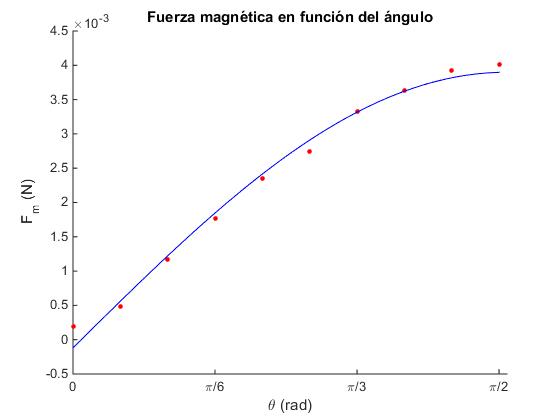
Fuerza en función del ángulo
| Intensidad (A) | 0.8 |
|---|---|
| Angulo θ | Fuerza magnética (N) |
| 0 | 0.196·10-3 |
| 10 | 0.490·10-3 |
| 20 | 1.176·10-3 |
| 30 | 1.764·10-3 |
| 40 | 2.352·10-3 |
| 50 | 2.744·10-3 |
| 60 | 3.332·10-3 |
| 70 | 3.626·10-3 |
| 80 | 3.920·10-3 |
| 90 | 4.018·10-3 |
Ajustamos los datos a la función no lineal A·sin(θ+φ) mediante la función MATLAB nlinfit. A partir del ajuste se determina A y φ
x=[0,10,20,30,40,50,60,70,80,90]*pi/180;
y=[0.196,0.490,1.176,1.764,2.352,2.744,3.332,3.626,3.920,4.018]/1000;
hold on
plot(x,y, 'o','markersize',3, 'markeredgecolor','r','markerfacecolor','r')
f_ajuste =@(a,x) a(1)*sin(x+a(2));
a0=[0.3 0]; %valor inicial de los parámetros
af=nlinfit(x,y,f_ajuste,a0)
%representa la función
x=linspace(0,90,40)*pi/180;
y=f_ajuste(af,x);
plot(x,y,'b')
set(gca,'XTick',0:pi/6:pi/2)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2'})
title('Fuerza magnética en función del ángulo')
xlabel('\theta (rad)')
ylabel('F_m (N)')
hold off
af = 0.0039 -0.0302
El parámetro A es a(1)=3.9·10-3, y el parámetro φ es a(2)=-0.0302