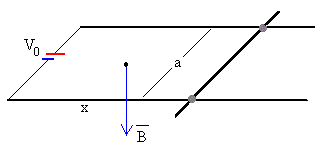
Una varilla desliza sin fricción sobre dos raíles paralelos distantes a en el seno de un campo magnético uniforme perpendicular al plano de los raíles.

Una batería cuya fem es V₀, los dos raíles y la varilla deslizante constituyen un circuito cerrado de resistencia R, la existente entre los dos puntos de contacto de la varilla con los raíles.

Ecuación del circuito

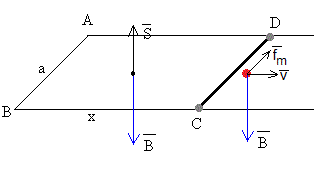
A medida que se mueve la varilla, aumenta el área y aumenta el flujo del campo magnético a través del circuito formado por los rieles y la varilla. La fem inducida V_ε de acuerdo a la ley de Faraday vale

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}}$

El flujo es, $\Phi =\overrightarrow{B}·\overrightarrow{S}=-B·a·x$

Derivando el flujo Φ respecto del tiempo y cambiando de signo

V_ε= B·a·v

Los portadores de carga positivos son empujados hacia el extremo D, que se carga positivamente

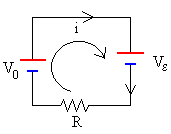
La ecuación del circuito es, la suma de fems es igual al producto de la intensidad por la resistencia total del circuito.

-V_ε+V₀=iR

Ecuación del movimiento de la varilla

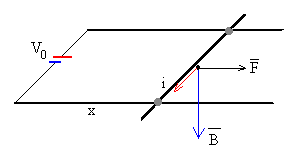
Una corriente i que circula por la porción de varilla de longitud a, experimenta una fuerza F en el seno de un campo magnético uniforme B.

${\displaystyle \overrightarrow{F}=i({\widehat{u}}_t\times \overrightarrow{B})a}$

donde ${\widehat{u}}_t$ es un vector unitario que señala la dirección y sentido del movimiento de los portadores de carga (positivos).

Como el campo magnético $\overrightarrow{B}$ es perpendicular a la varilla. El módulo de la fuerza es

F=iBa

Es un vector paralelo a los raíles y cuyo sentido es hacia la derecha, tal como se señala en la figura.

Si despreciamos la fuerza de rozamiento entre la varilla y los raíles, la ecuación del movimiento de la varilla de masa m es.

${\displaystyle m\frac{dv}{dt}=iBa}$

o bien,

${\displaystyle \frac{dv}{dt}=\frac{Ba}{mR}{V}_0-\frac{B^2{a}^2}{mR}v}$

• Velocidad de la varilla

La ecuación del movimiento se escribe

${\displaystyle \frac{dv}{dt}=\frac{v_f}{k}-\frac{v}{k}{v}_f=\frac{V_0}{Ba}k=\frac{mR}{B^2{a}^2}}$

Con las siguientes condiciones iniciales, en el instante t=0, v=0.

${\displaystyle k{\displaystyle \underset{0}{\overset{v}{\int }}\frac{dv}{v_f-v}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}v=v_f\left(1-\exp \left(-\frac{t}{k}\right)\right)}$

La velocidad aumenta desde cero, hasta que alcanza un valor límite constante v_f en un tiempo teóricamente infinito.

Un comportamiento similar al de una esfera que se mueve en el seno de un fluido viscoso.

• Intensidad de la corriente

Conocida la velocidad v determinamos la intensidad i de la corriente que circula por el circuito.

${\displaystyle iR=V_0-V_{\epsilon }i=\frac{V_0}{R}\exp \left(-\frac{t}{k}\right)}$

La intensidad disminuye exponencialmente con el tiempo. Se hace cero al cabo de un tiempo teóricamente infinito, en la práctica viene determinado por el valor de la constante de tiempo k.

• Posición de la varilla

Integrando con respecto del tiempo la expresión de la velocidad v, obtenemos la posición x de la varilla en función del tiempo t, con las condiciones iniciales siguientes: en el instante t=0, la varilla parte del origen x=0.

${\displaystyle {\displaystyle \underset{0}{\overset{x}{\int }}dx}={\displaystyle \underset{0}{\overset{t}{\int }}v·dt}x=v_{f}t-v_{f}k\left(1-\exp \left(-\frac{t}{k}\right)\right)}$

Estudio energético

• La energía suministrada por la batería entre el instante inicial t=0 y el instante t es

${\displaystyle E_0={\displaystyle \underset{0}{\overset{t}{\int }}{V}_{0}i·dt}=\frac{m{V}_0^2}{B^2{a}^2}\left(1-\exp \left(-\frac{t}{k}\right)\right)}$

• La energía disipada en la resistencia durante ese mismo tiempo es

${\displaystyle E_R={\displaystyle \underset{0}{\overset{t}{\int }}{i}^{2}R·dt}=\frac{1}{2}\frac{m{V}_0^2}{B^2{a}^2}\left(1-\exp \left(-\frac{2t}{k}\right)\right)}$

• La energía cinética de la varilla en el instante t es

${\displaystyle E_k=\frac{1}{2}m{v}^2=\frac{1}{2}\frac{m{V}_0^2}{B^2{a}^2}{\left(1-\exp \left(-\frac{t}{k}\right)\right)}^2}$

Comprobamos que

E₀=E_R+E_k

Una parte de la energía suministrada por la batería se disipa en la resistencia y la otra parte, se convierte en energía cinética de la varilla. Al cabo de un tiempo teóricamente infinito, la mitad de la energía suministrada por la batería se ha disipado en la resistencia y la otra mitad se ha convertido en energía cinética.

Actividades

Se introduce

• El campo magnético B (en gauss) en el control titulado Campo magnético
• La distancia entre los raíles a (en cm), en el control titulado Distancia raíles.
• El material del que está hecho la varilla que desliza, en el control titulado Material.
• La diferencia de potencial V₀ entre los terminales de la batería, se ha fijado en el programa y es de 0.001 V.
• La longitud de la varilla L se ha fijado en 50 cm

Se pulsa el botón titulado Empieza

El programa nos proporciona los datos de la densidad y resistividad de los materiales

Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física elemental. Edt Mir (1975), págs. 36, 139.

Ejemplo:

Elegimos como material el Aluminio

Introducimos

• el valor del campo magnético B=100 gauss=0.01 T
• la distancia entre raíles a=40 cm=0.4
• La masa de la varilla es m=ρ·L·S
• La resistencia de la porción de varilla comprendida entre los contactos con los rieles es R=r·a/S. Siendo S la sección de la varilla

La constante de tiempo k vale

${\displaystyle k=\frac{mR}{B^2{a}^2}=\frac{\rho rL}{B^{2}a}=\frac{2.7·{10}^3·0.028·{10}^{-6}·0.5}{{0.01}^2·0.4}=0.945\text{s}}$

La velocidad final v_f de la varilla es

${\displaystyle v_f=\frac{V_0}{Ba}=\frac{0.001}{0.01·0.4}=0.25\text{m/s}=25\text{cm/s}}$

Como podremos observar, al cabo de unos pocos segundos la varilla alcanza una velocidad constante, la intensidad tiende a cero.

Al lado de la varilla se dibujan los vectores campo magnético $\overrightarrow{B}$ , el vector ${\widehat{u}}_t$ que señala la dirección y sentido del movimiento de los portadores de carga. El vector fuerza $\overrightarrow{F}$ que ejerce el campo magnético sobre la corriente i que circula por la varilla.

• el campo magnético es constante
• la intensidad i disminuye con el tiempo, hasta que se hace cero
• la fuerza tiende a cero, y la velocidad de la varilla se hace constante e igual a la velocidad límite v_f.

La intensidad viene indicada por el movimiento de puntos de color rojo (portadores de carga positivos) a lo largo del circuito constituido por la batería, los raíles y la varilla.

A la izquierda, un diagrama nos señala en cada instante t:

• la energía cinética E_k de la varilla (un sector en color azul),
• la energía disipada en la resistencia E_R (un sector en color rojo),
• la suma de ambas, que es la energía suministrada por la batería, E_B, el círculo completo.

En la parte superior izquierda, se nos proporciona los datos relativos:

• El instante t en s.
• la posición x de la varilla en cm
• la velocidad v de la varilla en cm/s

Motor lineal

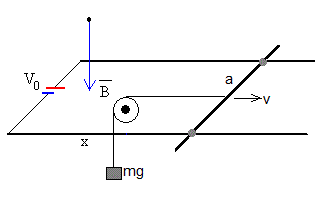
Consideremos de nuevo, el problema de la varilla que desliza sin fricción sobre dos raíles paralelos distantes a en el seno de un campo magnético uniforme perpendicular al plano de los raíles.

Una batería cuya fem es V₀, los dos raíles y la varilla deslizante constituyen un circuito cerrado de resistencia R, la existente entre los dos puntos de contacto de la varilla con los raíles.

En esta ocasión, la varilla se mueve con velocidad v constante. La fuerza que ejerce el campo magnético sobre la corriente que pasa por la varilla iBa, se emplea en levantar un peso, mg

• Al desplazarse la varilla, el flujo de campo magnético a través de la espira ABCD cambia con el tiempo, se genera una fem

V_ε= B·a·v

• La ecuación del circuito es

-V_ε+V₀=iR

• La fuerza que ejerce el campo magnético sobre la corriente que circula por la varilla es

F=iBa

Para que la varilla se mueva con velocidad constante, iBa=mg

Despejamos la velocidad v de la varilla

${\displaystyle \begin{array}{l}{V}_{\epsilon }=V_0-iR=V_0-\frac{mg}{Ba}R\\ Bav=V_0-\frac{mg}{Ba}R\\ v=\left(V_0-\frac{mg}{Ba}R\right)\frac{1}{Ba}\end{array}}$

Datos, V₀=15 V, a=10 cm, R=0.1 Ω, m=1.2 kg, B=1 T

v=32.4 m/s

Balance energético

• Energía por unidad de tiempo suministrada por la batería

${\displaystyle P_1=V_{0}i=V_0\frac{mg}{Ba}}$

• Energía por unidad de tiempo disipada en la resistencia

${\displaystyle P_2=i^{2}R={\left(\frac{mg}{Ba}\right)}^{2}R}$

• Energía mecánica por unidad de tiempo (potencia)

${\displaystyle P_3=Fv=mgv}$

Comprobamos que P₁=P₂+P₃

Rendimiento del motor

${\displaystyle \eta =\frac{P_3}{P_1}=\frac{mgv}{V_0\frac{mg}{Ba}}=1-\frac{mg}{Ba}\frac{R}{V_0}}$

Con los datos anteriores, η=21.6 %, un motor poco eficiente

Doble circuito

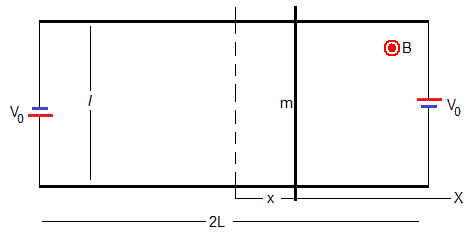
El doble circuito consiste en dos raíles paralelos de longitud 2L, separados una distancia l. Dos baterías de fem V₀ están conectadas a los extremos de los raíles. La resistencia de cada raíl es r. Una varilla de masa m y resistencia R desliza sin rozamiento sobre los raíles sin rozamiento.

Se supone que los cables que conectan las baterías a los extremos de los raíles carecen de resistencia

El circuito está situado sobre una tabla horizontal en el seno de un campo magnético uniforme B en la dirección vertical.

En la figura, se muestra la varilla en la posición x medida desde el origen que se establece en la mitad de los raíles (línea a trazos)

Vamos a deducir la ecuación del movimiento de la varilla

Ley de Faraday

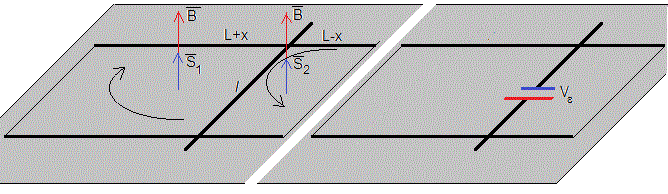
• Aplicamos la ley de Faraday al circuito de la izquierda de longitud L+x y anchura l

${\displaystyle \begin{array}{l}{\Phi }_1=\overrightarrow{B}·\overrightarrow{S_1}=B(L+x)l\\ V_1=-\frac{d{\Phi }_1}{dt}=-Bl\frac{dx}{dt}\end{array}}$

El flujo aumenta el sentido de la corriente inducida es horario

• Aplicamos la ley de Faraday al circuito de la derecha de longitud L-x y anchura l

${\displaystyle \begin{array}{l}{\Phi }_2=\overrightarrow{B}·\overrightarrow{S_2}=B(L-x)l\\ V_2=-\frac{d{\Phi }_2}{dt}=Bl\frac{dx}{dt}\end{array}}$

El flujo disminuye el sentido de la corriente inducida es antihorario

La varilla es equivalente a una batería de fem

${\displaystyle V_{\epsilon }=2Bl\frac{dx}{dt}=2Blv}$

Ecuación del circuito

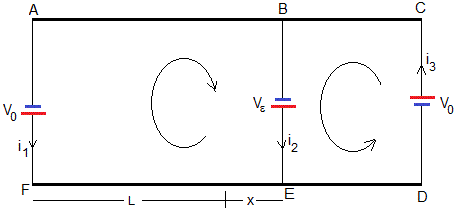
Las ecuaciones del circuito son

${\displaystyle \{\begin{array}{l}{V}_{\epsilon }-V_0=i_2{R}_{BE}-i_1\left(R_{AB}+R_{EF}\right)\\ V_{\epsilon }+V_0=i_2{R}_{BE}+i_3\left(R_{BC}+R_{DE}\right)\\ i_3=i_2+i_1\end{array}}$

R_AB=R_EF, R_BC=R_DE, R_BE=R

${\displaystyle R_{AB}=r\frac{L+x}{2L},R_{BC}=r\frac{L-x}{2L}}$

Resolvemos el sistema de tres ecuaciones y despejamos las intensidades i₁, i₂ y i₃

${\displaystyle \{\begin{array}{l}{V}_{\epsilon }-V_0=i_{2}R-2i_{1}r\frac{L+x}{2L}\\ V_{\epsilon }+V_0=i_{2}R+2i_{3}r\frac{L-x}{2L}\\ i_3=i_2+i_1\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}{i}_1=\frac{V_{0}R+\left(V_0-V_{\epsilon }\right)r\frac{L-x}{2L}}{Rr+r^2\frac{L^2-x^2}{2L^2}}\\ i_2=r\frac{V_{\epsilon }+V_0\frac{x}{L}}{Rr+r^2\frac{L^2-x^2}{2L^2}}\\ i_3=\frac{V_{0}R+\left(V_0+V_{\epsilon }\right)r\frac{L+x}{2L}}{Rr+r^2\frac{L^2-x^2}{2L^2}}\end{array}}$

Ecuación del movimiento

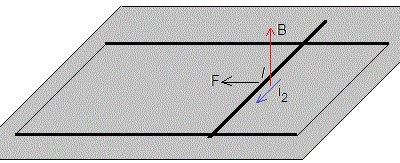
La fuerza que ejerce el campo magnético sobre una porción de corriente rectilínea es

${\displaystyle \overrightarrow{F}=i\left({\widehat{u}}_t\times \overrightarrow{B}\right)l}$

Por la varilla circula una corriente de intensidad i₂ en el sentido indicado en la figura, la fuerza sobre la varilla es

${\displaystyle F=-i_{2}Bl=-2L\frac{2B\frac{dx}{dt}lL+V_{0}x}{2L^{2}R+r\left(L^2-x^2\right)}Bl}$

La ecuación del movimiento

${\displaystyle m\frac{d^{2}x}{d{t}^2}+\frac{4{\left(BlL\right)}^2}{2L^{2}R+r\left(L^2-x^2\right)}\frac{dx}{dt}+\frac{2\left(BlL\right)V_0}{2L^{2}R+r\left(L^2-x^2\right)}x=0}$

que resoveremos por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante t=0, x=0, dx/dt=v₀. La varilla parte del origen con velocidad v₀

Aproximación

Si el desplazamiento de la varilla x es pequeño en relación con la mitad de la longitud L del raíl, x<<L

${\displaystyle m\frac{d^{2}x}{d{t}^2}+\frac{4{\left(Bl\right)}^2}{2R+r}\frac{dx}{dt}+\frac{2\left(Bl/L\right)V_0}{2R+r}x=0}$

Que corresponde a la ecuación de una oscilación amortiguada

${\displaystyle \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=\mathrm{0,}\{\begin{array}{l}\gamma =\frac{2}{m}\frac{{\left(Bl\right)}^2}{2R+r}\\ {\omega }_0^2=\frac{2}{mL}\frac{Bl}{2R+r}{V}_0\end{array}}$

La solución de esta ecuación diferencial con las condiciones iniciales, en el instante t=0, x=x₀, dx/dt=v₀, es

${\displaystyle x=\exp (-\gamma t)\left(\frac{v_0+\gamma x_0}{\omega }\sin (\omega t)+x_0\cos (\omega t)\right),{\omega }^2={\omega }_0^2-{\gamma }^2}$

Si la varilla parte del origen x₀=0 con velocidad v₀

${\displaystyle x=\frac{v_0}{\omega }\exp (-\gamma t)\sin (\omega t)}$

Energías

• Suministrada por las baterías

${\displaystyle E_1=V_0{\displaystyle \underset{0}{\overset{t}{\int }}(i_1+i_3)dt}}$

• Disipada en las resistencias

${\displaystyle E_2={\displaystyle \underset{0}{\overset{t}{\int }}\left(i_2^{2}R+i_1^{2}r\frac{L+x}{L}+i_3^{2}r\frac{L-x}{L}\right)dt}}$

• Variación de energía cinética de la varilla

${\displaystyle E_3=\frac{1}{2}m{v}^2-\frac{1}{2}m{v}_0^2}$

Ejemplos

Datos del doble circuito

• Longitud de los raíles, 2L= 2 m
• Distancia entre los dos raíles, l=0.5 m
• Resistencia de la longitud 2L del raíl, r=1 Ω
• Resistencia de la varilla, R=1 Ω
• Masa de la varilla, m=1 kg
• Velocidad inicial en el origen, v₀=0.1 m/s
• fem de cada batería, V₀=3 V
• Campo magnético vertical, B= 1 T

Resolvemos la ecuación diferencial del movimiento por el procedimiento ode45 de MATLAB, comparamos la solución numérica con la analítica aproximada (oscilaciones amortiguadas)

L=1; %longitud railes
l=0.5; %distancia entre raíles
r=1; %resistencia de cada raíl
R=1; %resistencia de la varilla
B=1; %campo magnético
V0=3; %fem de cada batería
v0=0.1; %velocidad inicial
m=1; %masa de la varilla
w0=sqrt(2*B*l*V0/(m*L*(2*R+r)));
gamma=2*(B*l)^2/(m*(2*R+r));
w=sqrt(w0^2-gamma^2);
f=@(t,x) [x(2);-4*(B*l*L)^2*x(2)/(2*L^2*R+r*(L^2-x(1)^2))-
2*B*l*L*V0*x(1)/(2*L^2*R+r*(L^2-x(1)^2))]; 
tf=2*2*pi/w0; %dos periodos
[t,x]=ode45(f,[0,2*2*pi/w0],[0,v0]);
hold on
plot(t,x(:,1))
fplot(@(t) v0*exp(-gamma*t).*sin(w*t)/w, [0, tf])
hold off
grid on
legend('numerico','analítico aprox.','location','best')
ylabel('x')
xlabel('t')
title('Movimiento varilla')

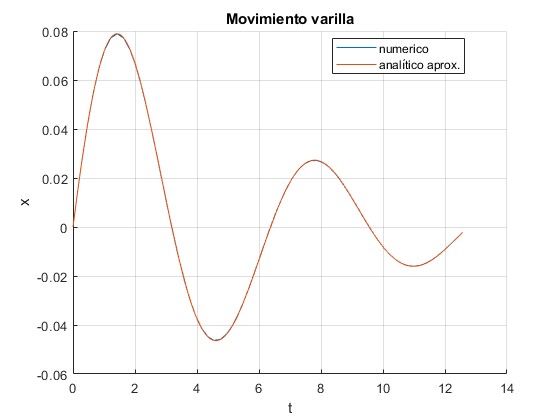
Observamos que ambas soluciones coinciden para este ejemplo, el máximo desplazamiento de la varilla es 8 cm muy pequeño comparado con la longitud de los raíles 2L= 2 m.

Calculamos las energías

• Producida por las baterías, E₁
• Disipada en las resistencias, E₂
• La variación de energía cinética, E₃

resoviendo las integrales definidas por procedimientos numéricos, empleando la función integral de MATLAB. Añadimos el siguiente código al script anterior

...
xx=@(t) v0*exp(-gamma*t).*sin(w*t)/w; %posición
v=@(t) v0*exp(-gamma*t).*(-gamma*sin(w*t)/w+cos(w*t)); %velocidad
i2=@(t) r*(2*B*v(t)*l+V0*xx(t)/L)/(R*r+r^2);
i1=@(t) (V0*R+((V0-2*B*v(t)*l)*r).*(L-xx(t))/(2*L))/(R*r+r^2/2);
i3=@(t) (V0*R+((V0+2*B*v(t)*l)*r).*(L+xx(t))/(2*L))/(R*r+r^2/2);
f1=@(t) i1(t)+i3(t);
f2=@(t) i2(t).^2*R+(i1(t).^2*r).*(L+xx(t))/L+(i3(t).^2*r).*(L-xx(t))/L;

E1=V0*integral(f1,0,tf);
E2=integral(f2,0,tf);
E3=m*v(tf)^2/2-m*v0^2/2;
disp([E1,E2,E3])

  226.1947  226.0871   -0.0049

La mayor parte de la energía producida por las baterías se disipa en la resistencias y solamente, una peqeña parte, se convierte en energía cinética de la varilla, E₁-E₂=E₃. El error en el procedimiento numérico puede ser mayor que E₃

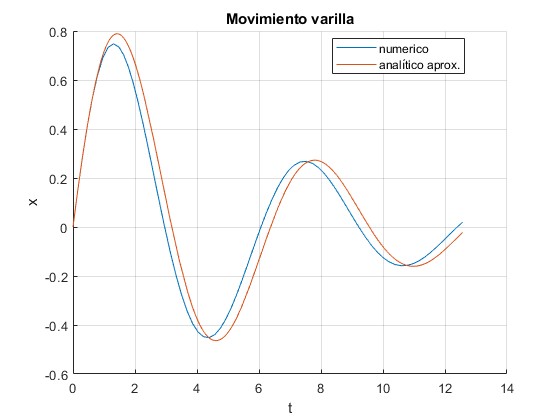
Ambas soluciones difieren cuando la condición x<<L deja de cumplirse, por ejemplo, cambiando la velocidad inicial de la varilla, v₀=1 m/s

Referencias

White III, J. Solution of a Faraday’s law problem including a nonlinear term. Am. J. Phys. 41 May 1973, pp. 644-647.

Walter Greiner. Classical Electrodynamics. Springer. pp. 247-249

Physics Challenge for Teachers and Students. From B or not from B. Physics Teacher 60, 389 (2022)