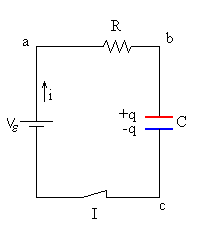
En el circuito de la figura tendremos que la suma

V_ab+V_bc+V_ca=0

• El extremo a tiene un potencial mayor que el extremo b de la resistencia R ya que la corriente fluye de a a b. De acuerdo a la ley de Ohm V_ab=iR
• La placa positiva del condensador b tiene mayor potencial que la placa negativa c, de modo que V_bc=q/C.
• El terminal positivo de la batería a tiene mayor potencial que el terminal negativo c, de modo que V_ca=-V_ε , donde V_ε es la fem de la batería

La ecuación del circuito es

${\displaystyle iR+\frac{q}{C}-V_{\epsilon }=0}$

Teniendo en cuenta que la intensidad se define como la carga que atraviesa la sección del circuito en la unidad de tiempo, i=dq/dt, tendremos la siguiente ecuación para integrar

${\displaystyle \begin{array}{l}R\frac{dq}{dt}=V_{\epsilon }-\frac{q}{C}\\ {\displaystyle \underset{0}{\overset{q}{\int }}\frac{dq}{C{V}_{\epsilon }-q}}=\frac{1}{RC}{\displaystyle \underset{0}{\overset{t}{\int }}dt}q=C{V}_{\epsilon }\left(1-\exp \left(\frac{-t}{RC}\right)\right)\end{array}}$

Derivando con respecto al tiempo, obtenemos la intensidad en función del tiempo

${\displaystyle i=\frac{dq}{dt}=\frac{V_{\epsilon }}{R}\exp \left(\frac{-t}{RC}\right)}$

La carga tiende hacia un valor máximo C·V_ε al cabo de un cierto tiempo, teóricamente infinito.

La intensidad disminuye exponencialmente con el tiempo, hasta que se hace cero cuando el condensador adquiere la carga máxima.

La cantidad RC que aparece en el denominador de t se denomina constante de tiempo del circuito. Éste, representa el tiempo que tomará a la corriente para decrecer hasta 1/e de su valor inicial.

Balance energético

• La energía aportada por la batería hasta el instante t es

${\displaystyle E_b={\displaystyle \underset{0}{\overset{t}{\int }}{V}_{\epsilon }i·dt}=V_{\epsilon }^{2}C\left(1-\exp \left(\frac{-t}{RC}\right)\right)}$

• La energía disipada en la resistencia hasta el instante t es

${\displaystyle E_R={\displaystyle \underset{0}{\overset{t}{\int }}{i}^{2}R·dt}=\frac{V_{\epsilon }^{2}C}{2}\left(1-\exp \left(\frac{-2t}{RC}\right)\right)}$

• La energía almacenada en el condensador en forma de campo eléctrico es

${\displaystyle E_c=\frac{1}{2}\frac{q^2}{C}=\frac{V_{\epsilon }^{2}C}{2}{\left(1-\exp \left(\frac{-t}{RC}\right)\right)}^2}$

Comprobamos que E_b=E_R+E_C. Parte de la energía suministrada en la batería se disipa en la resistencia y otra parte, se acumula en el condensador.

Cuando se completa el proceso de carga t→∞, la mitad de la energía suministrada por la batería se disipa en la resistencia y la otra mitad se acumula en el condensador.

Ejemplo:

Sea un condensador de capacidad C=1.5 µF en serie con una resistencia de R=58 kΩ y una batería de V_є=30 V. Empezamos a contar el tiempo cuando se cierra el interruptor. En el instante t=60 ms

• La carga del condensador es

${\displaystyle q=1.5·{10}^{-6}·30\left(1-\exp \left(\frac{-60·{10}^{-3}}{58000·1.5·{10}^{-6}}\right)\right)=22.42·{10}^{-6}\text{C}}$

• La intensidad es

${\displaystyle i=\frac{30}{58000}\exp \left(\frac{-60·{10}^{-3}}{58000·1.5·{10}^{-6}}\right)=2.60·{10}^{-4}\text{A}}$

• La energía suministrada por la batería es

${\displaystyle E_b=1.5·{10}^{-6}·{30}^2\left(1-\exp \left(\frac{-60·{10}^{-3}}{58000·1.5·{10}^{-6}}\right)\right)=6.73·{10}^{-4}\text{J}}$

• La energía disipada en la resistencia es

${\displaystyle E_R=\frac{1.5·{10}^{-6}·{30}^2}{2}\left(1-\exp \left(\frac{-2·60·{10}^{-3}}{58000·1.5·{10}^{-6}}\right)\right)=5.05·{10}^{-4}\text{J}}$

• La energía acumulada en el condensador es

${\displaystyle E_C=\frac{1}{2}\frac{{(22.42·{10}^{-6})}^2}{1.5·{10}^{-6}}=1.68·{10}^{-4}\text{J}}$

Cuando se completa el proceso de carga t→∞,

• La carga del condensador es

q=CV_є=1.5·10^-6·30=45μC

• La energía suministrada por la batería es

E_b=13.5·10^-4 J

• La energía acumulada en el condensador es

E_c=6.75·10^-4 J

• La energía total disipada en la resistencia es

E_R=6.75·10^-4 J

Actividades

Se introduce

• La capacidad C del condensador, en el control titulado Condensador
• La resistencia R, en el control titulado Resistencia
• La fem V_ε de la batería está fijada en el valor de 10

Se pulsa el botón titulado Nuevo

Se observa la carga del condensador, su color pasa gradualmente de blanco (sin carga) a rojo (carga positiva) y azul (carga negativa). A la derecha, se traza la gráfica de la carga q y de la intensidad i en función del tiempo.

Observar

• que la carga máxima no depende de la resistencia R,
• que la intensidad máxima no depende de la capacidad C

Elegir dos valores de la resistencia R₁ y R₂ y dos valores de la capacidad C₁ y C₂ de modo que R₁·C₁=R₂·C₂.

Práctica de laboratorio

En el laboratorio utilizamos el circuito mostrado en la fotografía, que consta de una batería, una pila estándar de 1.5 V, una resistencia de 15000 Ω y un condensador de 1000 μF. Seleccionamos carga (Charge) y medimos la diferencia de potencial entre los extremos del condensador V_bc con un sensor Voltage/Current de PASCO. El programa CAPSTONE recoge los datos, realiza la representación gráfica y el ajuste de dichos datos seleccionado en el menú Exponencial inversa.

${\displaystyle V_{bc}=\frac{q}{C}=V_{\epsilon }\left(1-\exp \left(-\frac{t}{RC}\right)\right)}$

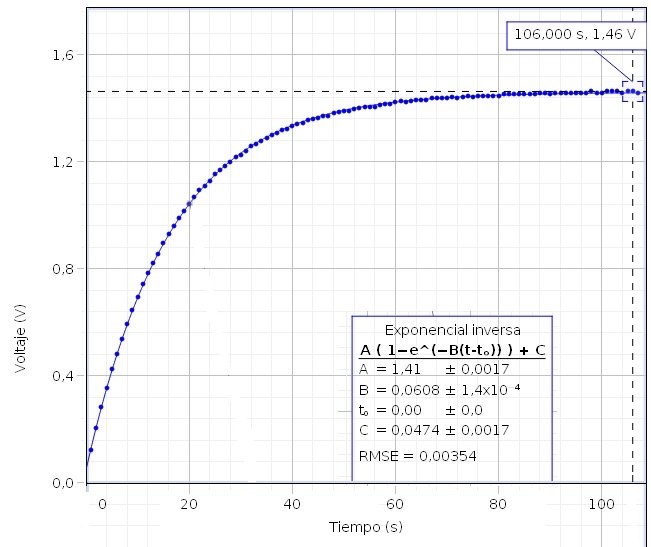
El parámetro B=0.0608, es igual a 1/RC donde R=15000 Ω, por lo que la capacidad del condensador es C=1.096·10^-3 F=1096 μF

Probamos con otro condensador

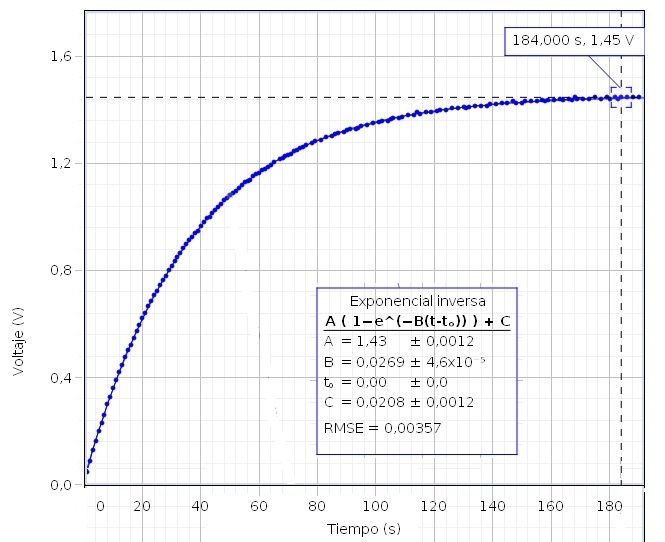
El parámetro B=0.0269, es igual a 1/RC donde R=15000 Ω, por lo que la capacidad del condensador es C=2478 μF

Condensadores en paralelo

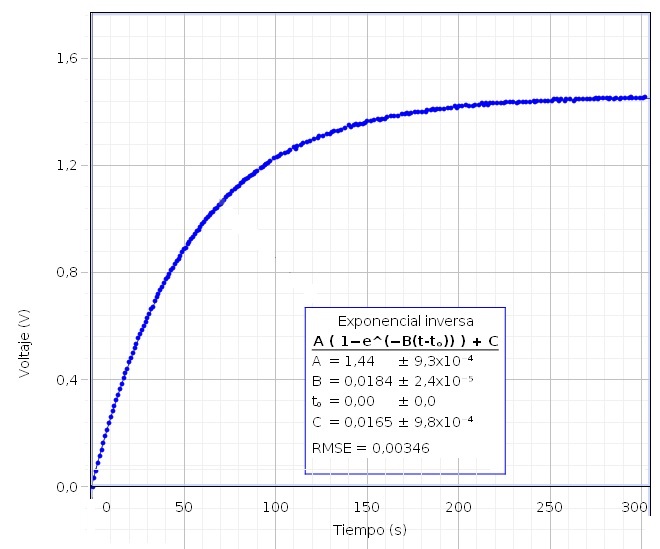
El parámetro B=0.0184, es igual a 1/RC donde R=15000 Ω, por lo que la capacidad del condensador equivalente es C_e=3623 μF

Cuando agrupamos dos condensadores en paralelo C₁=1096 μF y C₂=2478 μF, su capacidad equivalente se obtiene mediante la fórmula C_e=C₁+C₂=3574 μF

Condensadores en serie

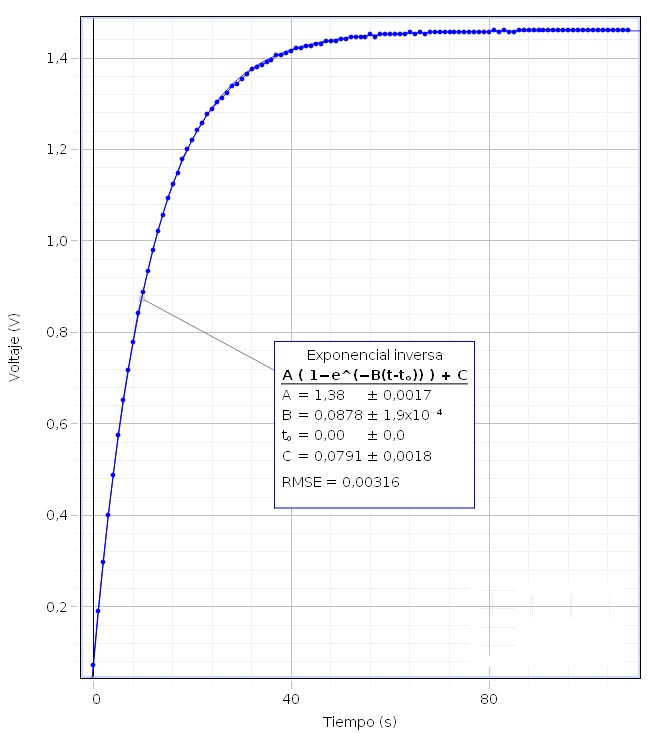
El parámetro B=0.0878, es igual a 1/RC donde R=15000 Ω, por lo que la capacidad del condensador equivalente es C_e=759 μF

Cuando agrupamos dos condensadores en serie C₁=1096 μF y C₂=2478 μF, su capacidad equivalente se obtiene mediante la fórmula

${\displaystyle \frac{1}{C_e}=\frac{1}{C_1}+\frac{1}{C_2}}$

El resultado es C_e=760 μF

Ajuste de datos con MATLAB

Vamos a utilizar MATLAB para realizar un ajuste no lineal de los datos experimentales (t,x) guardados en un fichero de texto generado por DataStudio

En primer lugar, preparamos los datos: Con el Bloc de Notas de Windows o similar, eliminamos la cabecera (dos líneas). Seleccionamos en el menú Edición/Reemplazar y sustituímos la coma (que separa la parte entera de los decimales) por un punto. Guardamos el fichero rc_1.txt, que se puede descargar en este enlace y lo colocamos en una carpeta accesible a MATLAB.

Elaboramos un script que realice las siguientes tareas:

1. Importar las dos columnas de datos con el comando load
2. Extraer la primera columna de los datos de tiempo y guardarla en el vector t
3. Extraer la segunda columna que corresponde a los datos de las diferencia de potencial V_bc y guardarlos en el vector x.
4. Representar los datos experiementales
5. Ajustar los datos a una función no lineal
6. Representar la función de ajuste en la misma ventana

Vamos a calcular la fem de la batería a₁=V_ε y la constante de tiempo a₂=1/RC, a partir del ajuste de datos por el procedimiento de mínimos cuadrados implementado en la función MATLAB nlinfit, tomando como modelo la función

${\displaystyle x=a_1\left(1-\exp (-a_{2}t)\right)}$

A la función nlinfit se le tiene que pasar:

• El vector de datos del tiempo y el vector de datos de la diferencia de potencial (tabla de datos experimentales)
• La definición del modelo de función
• Una estimación del valor inicial de los parámetros a₁, a₂

La función nlinfit devuelve el valor de dichos parámetros

Para la estimación de los valores iniciales, procedemos del siguiente modo: el primero de ellos a₁ es el valor al que tiende V_bc en la serie de datos, 1.5. El segundo a₂, lo tomamos de las características del cuircuito R=15000 Ω y C=1000 μF, por lo que a₂=1/RC=0.067.

Creamos un script para ajustar los resultados experimentales recogidos en la tabla de datos al modelo de función y obtener los valores de los parámetros a₁, a₂ a partir de los cuales calculamos la constante de tiempo 1/RC del circuito y la fem V_ε de la batería

load rc_1.txt
t=rc_1(:,1);
x=rc_1(:,2);
hold on
%representa los datos experimentales
plot(t,x,'o','markersize',2,'markerfacecolor','b')
%modelo de función
f_ajuste =@(a,t) a(1)*(1-exp(-a(2)*t));          
a0=[1.5 0.06];  %valor inicial de los parámetros
af=nlinfit(t,x,f_ajuste,a0)
%representa la función 
t=linspace(0,80,100);
x=f_ajuste(af,t);
plot(t,x,'r')
title('Carga de un condensador')
xlabel('tiempo (s)')
ylabel('Voltaje (V)')
grid on
hold off 

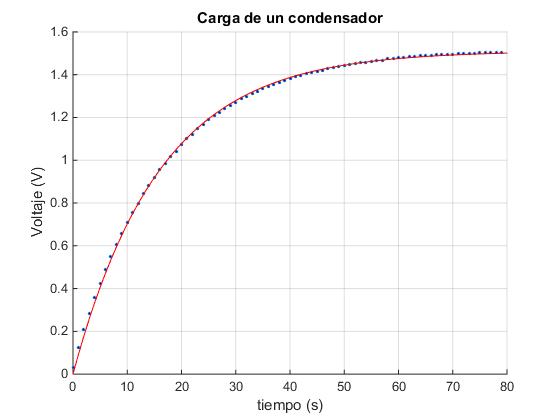
af =    1.5111    0.0625

La diferencia de potencial V_bc entre los extremos del condensador tiende hacia el valor 1.51 V y el cociente 1/RC=0.0625. Si la resistencia del circuito R=15000 Ω, la capacidad del condensador vale C=1067 μF