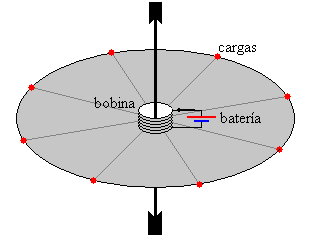
Imaginemos un dispositivo como el mostrado en la figura, que consta de un disco circular delgado hecho de plástico que puede girar alrededor de un eje perpendicular al plano del disco y que pasa por su centro. Se supondrá que la fricción en los apoyos de los extremos del eje es completamente despreciable.

En el centro del disco se coloca una pequeña bobina cuyo eje coincide con el eje de rotación del disco. Por la bobina pasa una corriente estacionaria de intensidad i, alimentada por una batería. En el borde del disco, y espaciadas uniformemente alrededor de su circunferencia hay un número de pequeñas esferas metálicas aisladas unas de las otras y del solenoide por el material plástico del disco. Cada una de las esferas conductoras está cargada con la misma carga q.

Inicialmente, el disco está en reposo. Supongamos que por algún accidente la corriente i en el solenoide se interrumpe. Por ejemplo, el solenoide se mantiene a muy baja temperatura de modo que el alambre del que está fabricado se hace superconductor. Cuando la temperatura se eleva por encima de la crítica, su resistencia aumenta y la corriente disminuye.

Al disminuir el flujo del campo magnético a través del solenoide se producirá un campo eléctrico inducido tangencial al perímetro del disco que actuará sobre las esferas cargadas, produciendo una fuerza, cuyo momento hará girar al disco.

Tenemos una situación similar a la descrita en la página dedicada al estudio del acelerador de partículas denominado betatrón. El campo eléctrico producido por el cambio del flujo del campo magnético en el tiempo acelera la partícula cargada

Aplicando el principio de conservación del momento angular, podemos decir, que el momento angular inicial del sistema aislado es cero, el momento angular final del conjunto será cero. Por tanto, no debe haber rotación del disco cuando la corriente desaparezca, esta es la paradoja.

Momento angular mecánico

Supongamos que la bobina tiene un radio a pequeño comparado con el radio R del disco. El campo producido por la bobina para puntos tales que r>>a es

${\displaystyle \overrightarrow{B}=\frac{{\mu }_0}{4\pi }\frac{3(\overrightarrow{m}·\overrightarrow{r})\overrightarrow{r}-r^2\overrightarrow{m}}{r^5}}$

Supondremos que la corriente i en el solenoide se modifica lentamente de modo que tenemos campos electromagnéticos cuasiestáticos en cada instante.

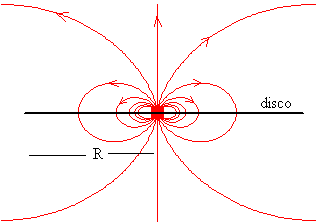
El flujo del campo magnético a través del plano infinito que contiene el disco es cero, ya que las líneas del campo magnético son cerradas. El flujo del campo magnético a través del área del disco, es igual y de signo contrario al flujo del campo magnético a través del área de la superficie del plano infinito al que se le ha restado el área del disco.

Fijarse que el cálculo directo del flujo a través del disco no es sencillo ya que no disponemos de una expresión de $\overrightarrow{B}$ para puntos en el interior de la bobina o cercanos a la misma.

Teniendo en cuenta que el momento magnético tiene la dirección del eje Z, $\overrightarrow{m}=m\widehat{k}$ , el campo $\overrightarrow{B}$ para los puntos del plano que contiene al disco z=0 es

${\displaystyle \overrightarrow{B}=-\frac{{\mu }_0}{4\pi }\frac{m}{y^3}\widehat{k}}$

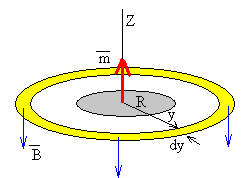
El flujo del campo magnético $\overrightarrow{B}$ a través del disco de radio R será,

${\displaystyle \Phi =-\underset{S}{{\displaystyle \int }}\overrightarrow{B}\cdot \overrightarrow{dS}=\frac{{\mu }_0}{4\pi }\underset{R}{\overset{\infty }{{\displaystyle \int }}}\frac{m}{y^3}2\pi y·dy=\frac{{\mu }_{0}m}{2R}}$

De acuerdo a la ley de Faraday

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dl}=-\frac{d}{dt}\underset{S}{{\displaystyle \int }}\overrightarrow{B}\cdot \overrightarrow{dS}}$

Debido a la simetría axial, el campo eléctrico $\overrightarrow{E}$ generado es constante en todos los puntos de una circunferencia de radio r, y su dirección es tangente a dicha circunferencia. El campo eléctrico E generado vale en la posición r=R del borde del disco donde se encuentran las cargas

${\displaystyle E·2\pi R=-\frac{{\mu }_0}{2R}\frac{dm}{dt}}$

Su sentido está determinado por la ley de Lenz, tal como se señala en la figura.

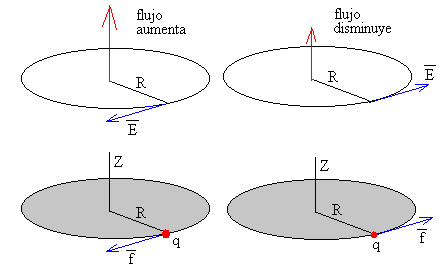
El campo eléctrico $\overrightarrow{E}$ ejerce una fuerza sobre la carga puntual q, $\overrightarrow{f}=q\overrightarrow{E}$

La fuerza $\overrightarrow{f}$ tiene la misma dirección que el campo $\overrightarrow{E}$, el mismo sentido si la carga q es positiva, y sentido contrario si la carga es negativa.

La fuerza $\overrightarrow{f}$, produce un momento que hace girar al disco. Si la carga total Q está uniformemente distribuida en el perímetro del disco, el momento M de la fuerza que ejerce el campo eléctrico $\overrightarrow{E}$ sobre las cargas es

${\displaystyle M=QER=-\frac{{\mu }_{0}Q}{4\pi R}\frac{dm}{dt}}$

El momento de una fuerza actuando durante un tiempo modifica el momento angular del sólido en rotación alrededor de un eje fijo.

El momento angular final del disco $\overrightarrow{L_{mec}}$ tiene la dirección del eje de rotación, y su módulo es

${\displaystyle L_{mec}={\displaystyle \underset{0}{\overset{\infty }{\int }}M·dt}=-\frac{{\mu }_{0}Q}{4\pi R}{\displaystyle \underset{0}{\overset{\infty }{\int }}dm=}\frac{{\mu }_{0}Q}{4\pi R}m}$

Siendo m el momento magnético inicial.

Momento angular de los campos electromagnéticos

La explicación de esta paradoja es que los campos eléctrico y magnético estáticos tienen momento angular. Dichos campos y el disco forman las dos partes de un sistema aislado que están acopladas por medio de las cargas en el borde del disco. Cuando cambia la corriente en la bobina, parte del momento angular almacenando en los campos se transforma en momento angular mecánico del disco.

El campo electromagnético en el vacío tiene un momento angular asociado con respecto al origen dado por la siguiente expresión

${\displaystyle \overrightarrow{L_{em}}=\frac{1}{c^2}\underset{V}{{\displaystyle \int }}(\overrightarrow{r}\times \overrightarrow{S})dV\overrightarrow{S}=\frac{1}{{\mu }_0}\overrightarrow{E}\times \overrightarrow{B}}$

Donde $\overrightarrow{S}$ es el vector de Poynting y c la velocidad de la luz en el vacío.

Después de algunas operaciones, cuya dificultad supera la de un curso introductorio de Física, se llega al resultado de que el momento angular del sistema formado por el disco y el campo electromagnético

${\displaystyle \overrightarrow{L_{mec}}+\overrightarrow{L_{em}}=0}$

como cabe esperar del principio de conservación del momento angular. Una parte del momento angular electromagnético se convierte en momento angular mecánico.

Si solamente están presentes las cargas, hay campo eléctrico pero no magnético, el momento angular $\overrightarrow{L}$ vale cero. Si solamente está presente la bobina por la que circula una corriente estacionaria, hay campo magnético pero no hay campo eléctrico, el momento angular es también cero. Cuando ambos campos están presentes el momento angular no es nulo.

Una deducción alternativa, se fundamenta en la fuerza que ejerce el campo magnético producido por la bobina sobre una carga puntual q que se trae desde el infinito hasta el borde del disco.

Supongamos que tenemos la bobina por la que circula una corriente estacionaria y las cargas eléctricas están en el infinito, no hay por tanto, momento angular. Movemos las cargas desde el infinito radialmente hacia el borde del disco con velocidad constante v.

Cuando una carga puntual q está a una distancia y del centro del disco, experimenta una fuerza $\overrightarrow{f}$ debido al campo magnético $\overrightarrow{B}$ producido por la bobina

${\displaystyle \begin{array}{l}\overrightarrow{B}=-\frac{{\mu }_0}{4\pi }\frac{m}{y^3}\widehat{k}\hfill \\ \overrightarrow{f}=q\overrightarrow{v}\times \overrightarrow{B}\overrightarrow{f}=\frac{{\mu }_{0}qmv}{4\pi y^3}\widehat{i}\hfill \end{array}}$

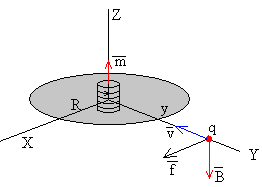
la dirección y sentido de la fuerza $\overrightarrow{f}$ están señalados en la figura

Para mover la carga q con velocidad constante hemos de ejercer una fuerza exterior. $\overrightarrow{f_{ext}}=-\overrightarrow{f}$ Esta fuerza produce un momento respecto del origen (el brazo de la fuerza es y), $\overrightarrow{r}=y\widehat{j}$

${\displaystyle \overrightarrow{M_{ext}}=\overrightarrow{r}\times \overrightarrow{f_{ext}}=\frac{{\mu }_{0}qmv}{4\pi y^2}\widehat{k}}$

El momento angular que almacena el campo electromagnético será

${\displaystyle L_{em}={\displaystyle \int M_{ext}dt}=\frac{{\mu }_{0}qm}{4\pi }{\displaystyle \underset{\infty }{\overset{R}{\int }}\frac{-dy}{y^2}=}\frac{{\mu }_{0}q}{4\pi R}m}$

Siendo v·dt=-dy. El vector $\overrightarrow{L_{em}}$ tiene la dirección del eje Z, y es independiente de la velocidad v con que se mueve la carga desde el infinito hasta el borde del disco.

Nota: una carga q al moverse con velocidad v produce un campo magnético, pero este campo no produce una fuerza sobre dicha carga en movimiento.

Simulación

La bobina se puede conectar o desconectar de la batería.

• Cuando la batería se conecta a la bobina, la corriente en la bobina crece hasta que se alcanza un valor constante i₀ después de un tiempo teóricamente infinito, en la práctica viene determinado por la constante de tiempo τ del circuito.

${\displaystyle i=i_0(1-\exp (-t/\tau ))}$

• Cuando la batería se desconecta de la bobina, la intensidad de la corriente no cae súbitamente a cero, sino que decrece exponencialmente con el tiempo, hasta que se hace cero después de un tiempo teóricamente infinito, en la práctica viene determinado por la constante de tiempo τ del circuito.

${\displaystyle i=i_0\exp (-t/\tau )}$

El momento magnético de la bobina es m=i·Nπa², donde N es el número de espiras, y a es el radio de las espiras.

El momento magnético m tiene el mismo comportamiento que la intensidad i. La razón de su cambio con el tiempo es

${\displaystyle \frac{dm}{dt}=\pm \frac{i_{0}N\pi a^2}{\tau }\exp \left(\frac{-t}{\tau }\right)}$

El signo positivo se obtiene cuando se conecta la batería a la bobina, y el negativo cuando se desconecta.

El momento de las fuerzas que ejerce el campo eléctrico generado sobre las cargas situadas en el bode del disco es

${\displaystyle M=\pm \frac{{\mu }_{0}Q}{4R}\frac{i_{0}N{a}^2}{\tau }\exp \left(\frac{-t}{\tau }\right)}$

Aplicando la ecuación de la dinámica de rotación, obtenemos el valor de la aceleración angular α, siendo I_c es el momento de inercia del disco.

${\displaystyle \alpha =k·\exp \left(\frac{-t}{\tau }\right)k=\pm \frac{{\mu }_{0}Q}{4R{I}_c}\frac{i_{0}N{a}^2}{\tau }}$

Integrando con respecto del tiempo, obtenemos la velocidad angular de rotación.

${\displaystyle \omega ={\displaystyle \underset{0}{\overset{t}{\int }}\alpha ·dt}=k\tau \left(1-\exp (-t/\tau )\right)}$

La velocidad angular final ω_f =kτ y el momento angular L no dependen de la constante de tiempo τ, y valen en módulo

${\displaystyle L=I_c{\omega }_f=\frac{{\mu }_{0}Q}{4\pi R}{i}_{0}N\pi a^2}$

El último factor, es el momento magnético inicial m=i₀·Nπa²

Integrando la velocidad angular ω respecto del tiempo obtenemos la posición angular θ.

${\displaystyle \theta ={\displaystyle \underset{0}{\overset{t}{\int }}\omega ·dt}=k\tau \left(t+\tau \exp (-t/\tau )\right)-k{\tau }^2}$

Cuando se alcanza la velocidad angular constante ω_f=kτ, el movimiento del disco es uniforme.

Actividades

Se introduce

• La constante del tiempo τ, en el control titulado Cte. tiempo
• El radio del disco R, en el control titulado Radio disco.
• El número de cargas puntuales que se sitúan en el bode del disco, en el control titulado Número de cargas.

El programa interactivo ha fijado, los valores de:

• el momento magnético inicial de la bobina i₀·Nπa²
• la carga q de cada una de las pequeñas esferas conductoras situadas en el borde del disco. La carga total es Q=n·q
• el momento de inercia I_c del disco

Se establece si

• la bobina está conectada o desconectada de la batería
• la carga es positiva o negativa

Se pulsa el botón titulado Nuevo

Se observa el movimiento de rotación del disco. En la parte superior derecha, se proporcionan los valores del tiempo t y de la velocidad angular de rotación ω en unidades arbitrarias.

Observaremos que

• la velocidad angular tiende hacia un valor límite constante.

• la velocidad angular final es proporcional al número de cargas n

• la velocidad angular final es inversamente proporcional al radio R (se supone que el momento de inercia I_c es constante e independiente del radio R)

Se muestra mediante vectores.

• El momento magnético $\overrightarrow{m}$ en el centro de la bobina. Aumenta cuando se conecta la batería y disminuye cuando se desconecta.
• El campo eléctrico $\overrightarrow{E}$, en la posición de una de las cargas en el borde del disco.
• La fuerza que ejerce dicho campo sobre una de las cargas positivas (en color rojo) o negativas (en color azul).