Energía y momento angular en un sistema electromecánico
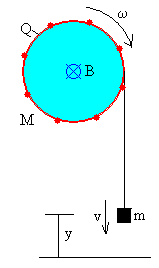
Consideremos una capa delgada aislante de forma cilíndrica de masa M, de longitud l y de radio R que puede girar libremente alrededor de su eje de simetría. Una carga Q se distribuye uniformemente en dicha capa.
Una cuerda inextensible y de masa despreciable se enrolla alrededor del cilindro y se cuelga de su extremo libre una masa m. En el instante inicial t=0 se libera el bloque de masa m.
El problema consiste, en determinar la aceleración del bloque, la energía cinética y el momento angular cuando el bloque ha descendido una altura h partiendo del reposo.
Toda carga acelerada radia energía en forma de ondas electromagnéticas. Se supondrá que la aceleración de las cargas es suficientemente pequeña para despreciar la pérdida de energía por radiación.
Movimiento cuando no hay carga
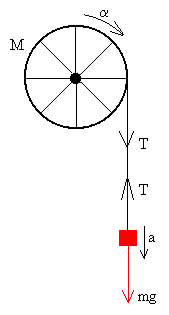
En la página titulada “Dinámica de rotación y balance energético” hemos analizado un sistema mecánico similar cuando Q=0.
En la figura, se han dibujado el esquema de las fuerzas sobre los cuerpos que intervienen en el movimiento.
- La ecuación de la dinámica de rotación del cilindro es
- La ecuación de la dinámica de traslación del bloque es
- La aceleración a del bloque es la misma que la aceleración tangencial αR de un punto de la superficie del cilindro.
T·R=Iα
mg-T=ma
a=α·R
La aceleración angular α vale
Cuando el bloque ha descendido una altura h partiendo del reposo, el ángulo girado por el cilindro es h/R. La velocidad angular de rotación ω es
Balance energético
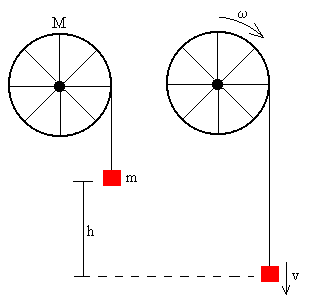
Cuando el bloque desciende una altura h partiendo del reposo, su energía potencial mgh se convierte en energía cinética de traslación del bloque y en energía cinética de rotación del cilindro.
La velocidad v del bloque es la misma que la de un punto de la superficie del cilindro. Por tanto, v=ωR. La velocidad angular ω final de rotación del cilindro es
El mismo valor que hemos obtenido aplicando las ecuaciones de la dinámica
Movimiento cuando hay carga en la capa cilíndrica
Campo magnético en el interior de la capa cilíndrica
La carga Q está uniformemente distribuida en una capa cilíndrica muy delgada. En el instante t gira con velocidad angular ω, produciendo una corriente
que atraviesa la sección lδ de la capa cilíndrica, siendo l la longitud del cilindro y δ el espesor de dicha capa.
Para obtener la expresión del campo magnético creado por la corriente i en el interior de la capa cilíndrica, aplicamos la ley de Ampère de un modo similar al de un solenoide. Supondremos
- que no hay campo magnético en el exterior de la capa cilíndrica
- que el campo magnético en el interior de la capa cilíndrica es uniforme y paralelo al eje Z del cilindro
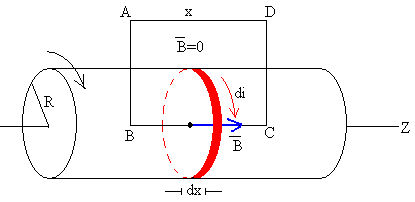
La circulación del campo magnético a lo largo del camino cerrado ABCD es Bz·x
La corriente que atraviesa el camino cerrado ABCD de longitud x es la misma que atraviesa la sección xδ de la capa cilíndrica, es decir, i·x/l
Aplicando la ley de Ampère despejamos el módulo del campo magnético
Energía magnética
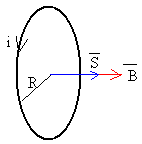
Del mismo modo que un solenoide, la capa cilíndrica tiene una autoinducción, que se calcula de un modo similar.
El campo magnético atraviesa la sección del circuito, que es equivalente a una espira por la circula una corriente de intensidad i
Se denomina coeficiente de autoinducción L al cociente entre el flujo propio F y la intensidad i.
La energía almacenada en forma de campo magnético en el interior del cilindro cuando gira con velocidad angular ω, es
Hay otra forma alternativa de obtener la energía magnética, multiplicando la densidad de energía magnética por el volumen del cilindro.
Ley de Faraday
Como la velocidad angular de rotación ω cambia con el tiempo, el campo magnético Bz cambia con el tiempo. El flujo de dicho campo a través de la capa esférica cambia con el tiempo. Aplicando la ley de Faraday
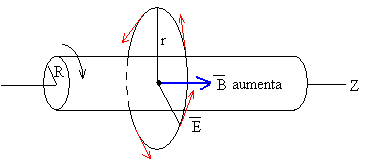
Como el campo magnético tiene la dirección del eje Z el campo eléctrico generado es tangente a la circunferencia de radio r cuyo centro está en el eje del cilindro, tal como se muestra en la figura.
El campo Eφ que en la posición r=R de la capa cilíndrica cargada vale
Ecuaciones del movimiento
Este campo produce una fuerza sobre las cargas, la fuerza produce un momento que tiende a frenar la rotación del cilindro. Suponiendo que la capa cilíndrica es muy delgada, la fuerza es EφQ, y el momento respecto del eje del cilindro (fuerza por su brazo R) es
M=RQEφ
- Sobre el cilindro actúan dos momentos de sentido contrario: el que produce la tensión de la cuerda y el que produce el campo eléctrico generado. La ecuación de la dinámica de rotación del cilindro es ahora
T·R+RQEφ=Ia
- La ecuación de la dinámica de traslación del bloque es
mg-T=ma
- La relación entre la aceleración angular α del cilindro y la aceleración a del bloque es
a=α·R
Despejando la aceleración angular α
La cantidad
tiene las dimensiones de momento de inercia, pero asociado con la carga Q no con la masa m, por esta razón se le denominará momento de inercia electromagnético Iem.
Como vemos la aceleración angular es menor que la que se obtiene cuando no hay carga en la capa cilíndrica Q=0.
La velocidad angular de rotación ω, cuando el bloque ha descendido una altura h partiendo del reposo es ahora
Balance energético
Cuando el bloque desciende una altura h partiendo del reposo, su energía potencial mgh se convierte en energía cinética de traslación del bloque, de rotación del disco, y el resto ΔE se almacena en forma de energía magnética en el interior de la capa cilíndrica tal como vamos a demostrar a continuación.
Calculamos esta diferencia
Se usa la fórmula de la velocidad angular ω calculada anteriormente, y se despeja mgh.
Sustituyendo el momento de inercia electromagnético Iem por su valor
La energía potencial mgh del bloque, se convierte en energía cinética del bloque, en energía cinética de rotación del disco y el resto se almacena en el interior de la capa cilíndrica como energía EB del campo magnético producido por el movimiento de las cargas situadas en dicha capa.
El principio de conservación de la energía se escribe para el caso Q≠0
Momento angular
El bloque de masa m, parte del reposo y el cilindro está en reposo en el instante inicial t=0. El momento angular inicial es cero.
Al cabo de un cierto tiempo t, el bloque desciende una altura h, moviéndose con velocidad v, la velocidad angular de rotación del cilindro es ω, y en el interior de la capa cilíndrica hay un campo magnético uniforme Bz.
El momento angular Lsis del sistema se obtiene a partir del impulso angular que es proporcionado por el bloque de masa m que cuelga del extremo de la cuerda enrollada en el cilindro.
Ponemos el momento angular del sistema Lsis como suma de dos contribuciones:
- el momento angular mecánico Lmec=(I+mR2)ω
- el momento angular electromagnético Lem=Iemω
Momento angular del campo electromagnético
El campo electromagnético en el vacío tiene un momento angular asociado con respecto al origen dado por la siguiente expresión
Donde es el vector de Poynting y c es la velocidad de la luz en el vacío.
Campo magnético
La distribución cilíndrica de carga al ponerse en movimiento de rotación produce un campo magnético paralelo al eje de rotación Bz que ya hemos calculado. Sin embargo, el campo magnético en el exterior del cilindro, aunque puede ser muy pequeño si el cilindro es suficientemente largo, no es nulo.
Campo eléctrico
La distribución cilíndrica de carga produce también un campo eléctrico que calcularemos aplicando la ley de Gauss.
Sea una capa cilíndrica delgada longitud l y de radio R uniformemente cargada con una carga Q. Para una distribución cilíndrica y uniforme de carga la aplicación del teorema de Gauss requiere los siguientes pasos:
- A partir de la simetría de la distribución de carga, determinamos la dirección del campo eléctrico.
-
Elegimos una superficie cerrada apropiada para calcular el flujo
- Determinamos la carga que hay en el interior de la superficie cerrada
- Región r<R
- Región r>R
La distribución de carga tiene simetría cilíndrica luego, la dirección del campo es radial y perpendicular al eje del cilindro.
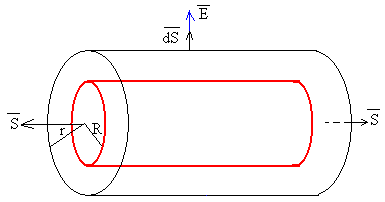
Tomamos como superficie cerrada, un cilindro de longitud l y de radio r.
El campo eléctrico es paralelo al vector superficie , y el campo es constante en todos los puntos de la superficie lateral cilíndrica como se ve en la figura, por lo que,
El flujo del campo eléctrico a través de las bases del cilindro es cero ya que es perpendicular a , tal como se muestra en la figura.
El flujo total es por tanto; E·2π rl
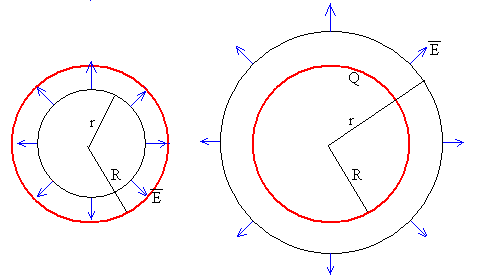
Como la carga está en la capa cilíndrica, la superficie cilíndrica de radio r<R no encierra ninguna carga. Luego, E=0.
La superficie cilíndrica de radio r>R encierra una carga Q, por lo que
Una vez conocidos los campos y , se procede a calcular el momento angular de los campos electromagnéticos estáticos. El resultado final de la integración que se omite, produce el mismo resultado Lem=Iem·ω.
Simulación
El momento de inercia electromagnético Iem es muy pequeño en un sistema real, ya que μ0=4π·10-7, y las carga por unidad de longitud que se puede acumular en una capa cilíndrica delgada es muy pequeña, inferior a 5·10-5 C/m, para un cilindro de 30 cm de radio.
El momento de inercia electromagnético Iem es proporcional al cuadrado de la carga Q. En la simulación asignaremos un valor arbitrario a la constante de proporcionalidad, de modo que Iem sea grande y comparable al momento de inercia mecánico mR2+I.
Ejemplo:
El momento de inercia de la capa cilíndrica es I=MR2
El momento de inercia electromagnético es Iem=k·Q2·R2. Se ha fijado el valor k=1/64 de la constante de proporcionalidad.
La aceleración angular depende del radio R, que se ha fijado en el valor R=30 cm.
La velocidad final de rotación ω es
Para m=0.3 kg, M=0.2 kg, Q=3 unidades de carga, h=1.0 m, R=0.3 m,
- La aceleración angular es α=4.59 rad/s2
- La velocidad angular final es ω=10.09 rad/s
Energía:
- La energía cinética de traslación del bloque vale E1=1.38 J
- La energía cinética de rotación del cilindro vale E2=0.92 J
- La energía electromagnética vale E3=0.64 J
La energía total es E=E1+E2+E3=2.94 J, que es la energía potencial inicial del bloque E=0.3·9.8·1.0=2.94 J
Fijarse que cuanto mayor sea la carga Q, menor es la velocidad angular final ω. La energía electromagnética es mayor y menor la energía cinética.
Momento angular:
- El momento angular mecánico es Lmec=(mR2+MR2)· ω=0.454 kg·m2/s
- El momento angular electromagnético Lem=Iem· ω=0.128 kg·m2/s
- El momento angular total del sistema es Lsis =Lem + Lmec =0.582 kg·m2/s
El tiempo que tarda el bloque en descender h=1.0 m partiendo del reposo es t=0.66 s
El impulso angular de la fuerza exterior (el peso del bloque) es mgR·t=0.58 kg·m2/s
Actividades
Se introduce
- La masa m del bloque en g, en el control titulado Masa bloque
- La masa M del cilindro en g, en el control titulado Masa cilindro
- La carga Q uniformemente distribuida en la capa cilíndrica muy delgada de radio R, en el control titulado Carga
Se pulsa el botón titulado Nuevo
- Se observa el movimiento de traslación del bloque y el movimiento de rotación del cilindro
- Se señala mediante puntos de color rojo, las cargas uniformemente distribuidas en la capa cilíndrica. Su movimiento en el sentido de las agujas del reloj, indica el sentido de la corriente.
- En color azul se señala el campo magnético, un aspa indica que su sentido es hacia dentro (regla de la mano derecha)
En la parte derecha, un diagrama en forma de tarta muestra como se va transformando la energía potencial inicial del bloque (color gris)
- energía cinética de traslación del bloque (color rojo)
- de rotación del cilindro (color rosa)
- en energía electromagnética almacenada en forma de campo magnético en el interior de la capa cilíndrica (color azul).
Referencias
Gauthier N. A Newton-Faraday approach to electromagnetic energy and angular momentum storage in an electromechanical system. Am. J. Phys. 70 (10) October 2002, pp. 1034-1038

