Autoinducción. Circuito R-L
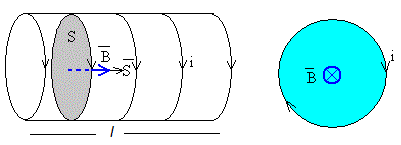
Supongamos un solenoide de N espiras, de longitud l y de sección S recorrido por una corriente de intensidad i.
El campo magnético producido por la corriente que recorre el solenoide es uniforme y paralelo a su eje, cuyo módulo hemos obtenido aplicando la ley de Ampère
Este campo atraviesa las espiras el solenoide, el flujo de dicho campo a través de todas las espiras del solenoide se denomina flujo propio.
Se denomina coeficiente de autoinducción L al cociente entre el flujo propio Φ y la intensidad i.
El coeficiente de autoinducción solamente depende de la geometría del circuito y de las propiedades magnéticas de la sustancia que se coloque en el interior del solenoide. La autoinducción de un solenoide de dimensiones dadas es mucho mayor si tiene un núcleo de hierro que si se encuentra en el vacío
La unidad de medida de la autoinducción se llama henry, abreviadamente H, en honor a Joseph Henry.
f.e.m. autoinducida
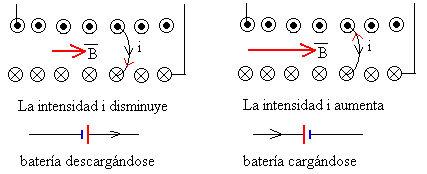
Cuando la intensidad de la corriente i cambia con el tiempo, se induce una f.e.m. en el propio circuito (flecha de color rojo) que se opone a los cambios de flujo, es decir de intensidad.
Derivando respecto al tiempo la expresión del flujo propio
La fem autoinducida VL siempre actúa en el sentido que se opone a la variación de corriente.
Ecuación del circuito RL
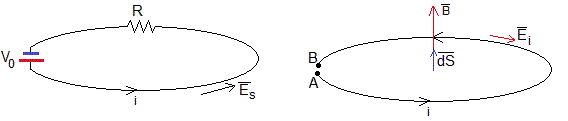
Sea un circuito de resistencia R, unido a una batería
Se sitúa las N espiras del circuito en el seno de un campo magnético B que aumenta con el tiempo.
La diferencia de potencial V0 en la batería produce una campo eléctrico que mueve las cargas produciendo una corriente i. La ley de Ohm, V0=iR
La ley de Faraday
donde es el campo eléctrico inducido que es no conservativo, al ser la integral a lo largo de un camino cerrado, distinta de cero.
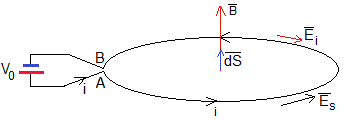
La combinación de ambos, es un circuito de N espiras, de resistencia R, conectado a una batería V0. El campo eléctrico total es
El campo eléctrico total, mueve las cargas en el conductor produciendo una intensidad i. La primera integral es el producto de la intensidad por la resistencia, iR.
es el campo eléctrico producido por la diferencia de potencial V0 de la batería, la segunda integral, es V0
Para N espiras iguales
Siendo Φ el flujo propio y L el coeficiente de autoinducción
El resultado final es
Establecimiento de una corriente en un circuito
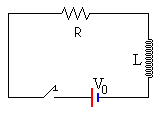
Cuando se aplica una fem V0 a un circuito cerrando un interruptor, la corriente no alcanza instantáneamente el valor V0/R dado por la ley de Ohm, sino que tarda un cierto tiempo, teóricamente infinito, en la práctica, un intervalo de tiempo que depende de la resistencia.
La razón de este comportamiento hay que buscarla en el papel jugado por la autoinducción L que genera una fem que se opone al aumento de la corriente en el circuito.
En la figura, se muestra un circuito formado por una batería, una resistencia y una autoinducción. Se conecta la batería y la intensidad i aumenta con el tiempo.
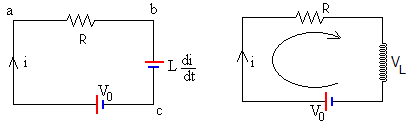
Para formular la ecuación del circuito sustituimos la autoinducción por una fem equivalente. Medimos la diferencia de potencial entre los extremos de cada uno de los tres elementos que forman el circuito. Se cumplirá que
La ecuación del circuito se obtiene de forma alternativa
Integrando, hallamos la expresión de i en función del tiempo con las condiciones iniciales t=0, i=0.
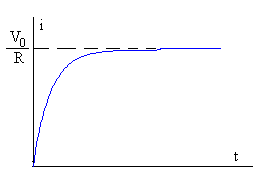
Si R/L es grande, como sucede en la mayor parte de los casos prácticos, la intensidad de la corriente alcanza su valor máximo constante V0/R en muy poco tiempo. Cuando se alcanza el estado estacionario, t→∞, la autoinducción no afecta al circuito ya que di/dt→0
Caída de la corriente en un circuito
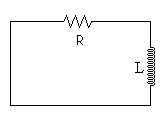
Si se ha establecido la corriente máxima en el circuito y desconectamos la batería, la corriente no alcanza el valor cero de forma instantánea, sino que tarda cierto tiempo en desaparecer del circuito. De nuevo, la razón de este comportamiento hay que buscarla en el papel jugado por la autoinducción L en la que se genera una fem que se opone a la disminución de corriente.
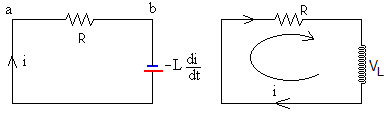
Para formular la ecuación del circuito sustituimos la autoinducción por una fem equivalente. Medimos la diferencia de potencial entre los extremos de cada uno de los dos elementos que forman el circuito. Se ha de tener en cuenta, que i disminuye con el tiempo por lo que su derivada di/dt<0 es negativa
La ecuación del circuito se obtiene de forma alternativa
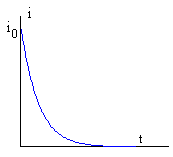
Integrando, hallamos la expresión de i en función del tiempo con las condiciones iniciales t=0, i=i0.
La corriente disminuye exponencialmente con el tiempo. En la mayor parte de los casos, R/L es grande, por lo que la corriente desaparece muy rápidamente.
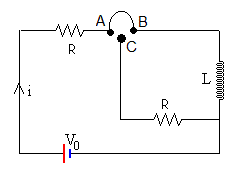
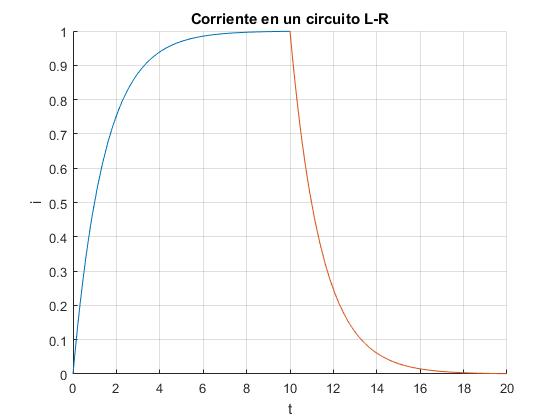
Diseñamos un experimento para mostrar el establecimiento y caída de una corriente en un circuito. Conectamos A y B, y cuando la corriente i es casi constante y aproximadamente, igual a V0/R, conectamos B y C, la corriente i decrece rápidamente
f=@(t) (1-exp(-0.7*t));
g=@(t) exp(-0.7*(t-10));
hold on
fplot(f,[0,10])
fplot(g,[10,20])
hold off
xlabel('t')
ylabel('i')
title('Corriente en un circuito L-R')
grid on
Energía del campo magnético
Hemos visto que para mantener una corriente en un circuito es necesario suministrar energía. La energía suministrada por la batería en la unidad de tiempo es V0·i. Esta energía se disipa, en la resistencia por efecto Joule y se acumula en la autoinducción en forma de energía magnética. De la ecuación del circuito
iR=V0+VL
Multiplicando ambos miembros por la intensidad i.
El término R·i2 es la energía por unidad de tiempo disipada en la resistencia. El primer término V0·i es la energía suministrada por la batería. El último término, es la energía por unidad de tiempo que se necesita para establecer la corriente en la autoinducción o su campo magnético asociado.
Simplificando dt e integrando entre 0 e i, obtenemos
Esta es la energía acumulada en forma de campo magnético, cuando circula por la bobina una corriente de intensidad i.
Para un solenoide la energía en forma de campo magnético que guarda en su interior se escribe
La energía EB es el producto de dos términos: la densidad de energía magnética (energía por unidad de volumen) y el volumen S·l. En general, la energía asociada a un campo magnético se calcula mediante la siguiente fórmula
La integral se extiende a todo el espacio donde el campo magnético es no nulo.
Comprobación
-
Cuando se cierra el circuito
- Cuando se abre el circuito y cae la corriente, toda la energía acumulada en la autoinducción se disipa en la resistencia.
La energía suministrada por la batería hasta el instante t es
La energía disipada en la resistencia es
La energía acumulada en la autoinducción en forma de campo magnético es
Comprobamos que E0=ER+EB
La energía inicial acumulada en la bobina, cuando la intensidad es i0
Al abrir el circuito la intensidad disminuye exponencialmente con el tiempo. La energía por unidad de tiempo disipada en la resistencia por efecto Joule será P=i2R
Integrando entre cero e infinito obtenemos la energía total disipada.
Coeficiente de autoinducción
Calculamos el coeficiente de autoinducción a partir de la energía del campo magnético
Solenoide
Supongamos un solenoide de N espiras, de longitud l y de sección S recorrido por una corriente de intensidad i. La dirección del campo magnético es paralela al eje del solenoide y su módulo es aproximadamente constante (véase el primer apartado)
La energía del campo magnético contenida en el volumen del solenoide es
Despejamos el coeficiente de autoinducción L
Cable
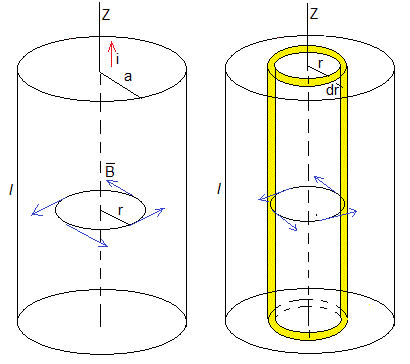
La corriente i está distribuida uniformemente por su sección circular de radio a de un cable muy largo
Se aplica la ley de Ampère para calcular el campo magnético en los puntos a una distancia r del eje (problema 4)
ir es la intensidad que atraviesa la circunfeencia de radio r<a del cable, que es una parte de la intensidad i
Para calcular la energía integramos sobre el volumen de una capa cilíndrica de longitud l y de radio comprendido entre r y r+dr, en esta capa el módulo del campo magnético es constante, dV=2πr·dr·l
Cable coaxial
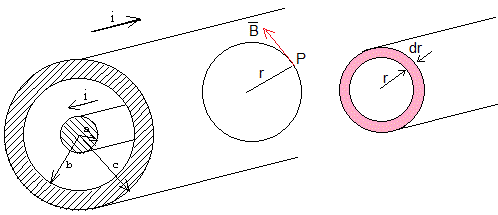
Se tienen dos cilindros de longitud muy grande concéntricos, uno de ellos hueco por el que circula una corriente i uniformemente distribuida en su sección y por el otro, circula la misma corriente pero en sentido contrario, estando también distribuida uniformemente por su sección. Se aplica la ley de Ampère para calcular el campo magnético en los puntos a una distancia r del eje (problema 5). El resultado es
La dirección del campo magnético en el punto P es perpendicular al plano determinado por el eje de la corriente cilíndrica y el punto P, es decir, tangente a la circunferencia de radio r con centro en el eje y que pasa por el punto P. El sentido lo determina la regla de la mano derecha
Para calcular la energía integramos sobre el volumen de una capa cilíndrica de longitud l y de radio comprendido entre r y r+dr, en esta capa el módulo del campo magnético es constante, dV=2πr·dr·l
Denominamos L' (H/m) al coeficiente de autoinducción por unidad de longitud
Actividades
Se introduce
- La autoinducción L de la bobina, en el control titulado Autoinducción
- La resistencia R del circuito, en el control titulado Resistencia
- La fem de la batería V0, en el control titulado Batería
Conectamos el circuito formado por la autoinducción y la resistencia a una batería, activando la casilla titulada Batería. Observamos como la intensidad de la corriente crece con el tiempo hasta que se establece una intensidad constante e igual a V0/R. La resistencia se va calentando pasando de color negro a rojo
Desactivamos la casilla Batería, la corriente inicial del circuito i0=V0/R, va disminuyendo exponencialmente con el tiempo hasta que desaparece. La resistencia se va enfriando pasando de color rojo a negro
Ejemplo. Circuito R, L
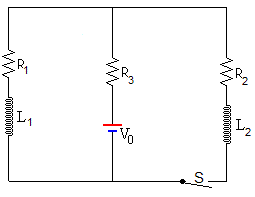
Consideremos el circuito de la figura, formado por una batería V0 de diferencia de potencial constante, una resistencia R3 y dos bobinas en paralelo de coeficientes de autoinducción L1 y L2, de resistencias internas R1 y R2, respectivamente. En el instante inicial t=0, se cierra el interruptor S y se mide la intensidad de la corriente que pasa por las bobinas.
Este ejemplo, ilustra el papel de la autoinducción en el establecimiento de una corriente constante en el circuito después de un tiempo teóricamente infinito, t→∞
Situación inicial
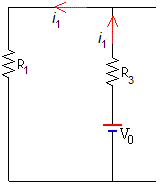
Antes de cerrar el interruptor, por la malla izquierda circula una corriente de intesidad i1, que después de un tiempo, ha alcanzado el estado estacionario (la autoinducción L1 no afecta al circuito), se ha hecho constante e igual a
Por la malla derecha no circula intensidad alguna, i2=0.
Estas son las intensidades que hay en el circuito en el instante t=0, cuando se cierra el interruptor S.
Situación final, estado estacionario
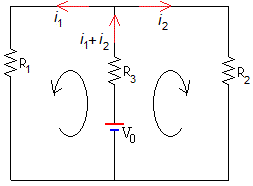
Después de un tiempo suficientemente grande t→∞, las corrientes i1 e i2 son constantes, las autoinducciones L1 y L2 no afectan al circuito
La ecuación de la malla izquierda es
La ecuación de la malla derecha es
-V0+(i1+i2)R3+i1R1=0
-V0+(i1+i2)R3+i2R2=0
Resolvemos el sistema de dos ecuaciones con dos incógnitas
De la situación inicial a la final
Estudiamos la evolución desde el estado inicial al final. Supondremos que i1 e i2 aumentan con el tiempo. Para formular la ecuación del circuito, sustituimos cada autoinducción por una batería del la misma fem que se está cargando
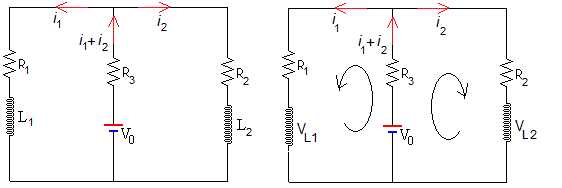
La ecuación de la malla izquierda y derecha son, respectivamente
La resistencia R3 actúa de acoplamiento entre las dos mallas. Si no existiese esta resistencia, tendríamos dos ecuaciones diferenciales separadas una para i1 y otra para i2
Tenemos que resolver un sistema de dos ecuaciones diferenciales con las siguientes condiciones iniciales, en el instante t=0, i2=0, i1=V0/(R1+R3). Introduciendo estas condiciones en el sistema de dos ecuaciones, tenemos dos condiciones más relativas a la derivada de las intensidades con respecto del tiempo
Despejamos i2 en la primera ecuación del sistema de dos ecuaciones diferenciales y la sustituimos en la segunda
Despejamos i1 en la segunda ecuación del sistema de dos ecuaciones diferenciales y la sustituimos en la primera
Las soluciones de las dos ecuaciones diferenciales lineales son
Las derivadas con respecto del tiempo t, son
Donde r1 y r2 son las raíces de la ecuación característica
Conocidas las expresiones de los coeficientes A y B, no resulta difícil demostrar que ambas raíces son reales y también, son negativas
Los coeficientes C1, C2, se determinan a partir de las condiciones iniciales: la intensidad i1(0) en el instante t=0 y de su derivada primera (di1/dt)0=0
Los coeficientes D1, D2, se determinan a partir de las condiciones iniciales: la intensidad i2(0)=0 en el instante t=0 y de su derivada primera (di2/dt)0
Representamos i1(t), i2(t) e i3(t)=i1+i2, para el siguiente circuito
- Bobina izquierda, autoinducción, L1=4.0 H, resistencia interna, R1=89 Ω
- Bobina derecha, autoinducción, L2=4.0 H, resistencia interna, R2=89 Ω
- Resistencia, R3=200 Ω
- Batería, diferencia de potencial constante, V0=9.3 V
L1=4; %bobina 1
R1=89;
L2=4; %bobina 2
R2=89;
R3=200; %resistencia
V0=9.3; %batería
A=L1*L2/(R1*R2+R1*R3+R2*R3);
B=(L1*(R2+R3)+L2*(R1+R3))/(R1*R2+R1*R3+R2*R3);
i1_0=V0/(R1+R3); %intensidad inicial
i1_inf=R2*V0/(R1*R2+R1*R3+R2*R3); %intensidad final
i2_inf=R1*V0/(R1*R2+R1*R3+R2*R3);
%raíces de la ecuación característica
r1=(-B+sqrt(B^2-4*A))/(2*A);
r2=(-B-sqrt(B^2-4*A))/(2*A);
C1=-(B/sqrt(B^2-4*A)+1)*(i1_inf-i1_0)/2;
C2=(B/sqrt(B^2-4*A)-1)*(i1_inf-i1_0)/2;
D2=(r1*i2_inf+R1*V0/(L2*(R1+R3)))/(r2-r1);
D1=(r2*i2_inf+R1*V0/(L2*(R1+R3)))/(r1-r2);
i1=@(t) (i1_inf+C1*exp(r1*t)+C2*exp(r2*t));
i2=@(t) (i2_inf+D1*exp(r1*t)+D2*exp(r2*t));
i3=@(t) i1(t)+i2(t);
hold on
fplot(i1,[0,0.1]) %100 ms
fplot(i2,[0,0.1])
fplot(i3,[0,0.1])
line([0,0.1],[i1_inf,i1_inf], 'lineStyle','--','color','k') %asíntota
hold off
grid on
xlabel('t (s)')
legend('1','2','3','Location','best')
ylabel('i(t)')
title('Intensidades')
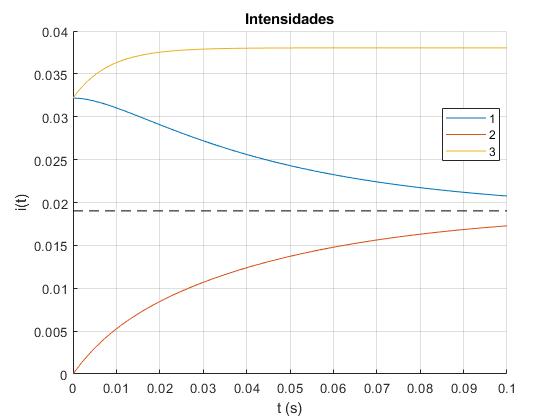
Observamos que las intensidades tienden hacia un valor constante, i1(∞)=i2(∞) señalado por la línea horizontal a trazos
Bobinas iguales L1=L2, R1=R2
Las expresiones de las intensidades se simplifican notablemente
Las raíces de la ecuación característica son
Las intensidades valen
Obtenemos la misma gráfica de las intensidades con el siguiente código
R=89;
L=4;
R3=200;
V0=9.3;
T=100/1000; %100 ms
hold on
i1=@(t) V0*(1+(-R*exp(-(R+2*R3)*t/L)+(R+2*R3)*exp(-R*t/L))/(2*(R+R3)))/(R+2*R3);
%V0/(R+2*R3)-V0*R*exp(-(R+2*R3)*t/L)/(2*(R+R3)*(R+2*R3))+V0*exp(-R*t/L)/(2*(R+R3));
fplot(i1,[0,T])
i2=@(t) V0*(1-(R*exp(-(R+2*R3)*t/L)+(R+2*R3)*exp(-R*t/L))/(2*(R+R3)))/(R+2*R3);
%V0/(R+2*R3)-V0*R*exp(-(R+2*R3)*t/L)/(2*(R+R3)*(R+2*R3))-V0*exp(-R*t/L)/(2*(R+R3));
fplot(i2,[0,T])
i3=@(t) V0*(2-R*exp(-(R+2*R3)*t/L)/(R+R3))/(R+2*R3); %i1(t)+i2(t);
fplot(i3,[0,T])
i_inf=V0/(R+2*R3);
line([0,T],[i_inf,i_inf],'lineStyle','--')
hold off
xlabel('t(s)')
ylabel('i(t)')
legend('1','2','3','Location','best')
grid on
title('Intensidades')
Energías
Energía producida por la batería entre el instante t=0 y el instante T
Energía disipada en las resistencias entre el instante t=0 y el instante T
Energía almacenada en las bobinas en el instante T
Como la intensidad inicial i1(0) no es nula e pero i2(0)=0, la bobina de la izquierda almacenaba una energía
De la energía proporcionada por la batería, una parte se disipa en las resistencias y otra parte, se almacena en forma de campo magnético en las bobinas
EV=ER+EL-EL0
Las integrales no son complicadas, podemos efectuarlas a mano, pero resulta muy laborioso, por lo que utilizamos el procedimiento numérico
Añadimos al script anterior, las líneas de código
... i1_2=@(t) i1(t).^2; i2_2=@(t) i2(t).^2; i3_2=@(t) i3(t).^2; E_V=integral(i3,0,T)*V0; %batería E_R=integral(i1_2,0,T)*R+integral(i2_2,0,T)*R+integral(i3_2,0,T)*R3; %resistencias E_L=L*(i1_2(T)+i2_2(T))/2; %autoinducción i0=V0/(R+R3); E_L0=i0^2*L/2; %inicial disp([E_V, E_R+E_L-E_L0])
0.0349 0.0349
Alternativamente, utilizamos Math Symbolic
syms t R R3 L V0;
i1=V0*(1+(-R*exp(-(R+2*R3)*t/L)+(R+2*R3)*exp(-R*t/L))/(2*(R+R3)))/(R+2*R3);
i2=V0*(1-(R*exp(-(R+2*R3)*t/L)+(R+2*R3)*exp(-R*t/L))/(2*(R+R3)))/(R+2*R3);
i3=i1+i2;
E_V=int(i3,t, 0,t)*V0; %batería
E_R=int(i1^2,t, 0,t)*R+int(i2^2,t, 0,t)*R+int(i3^2,t, 0,t)*R3; %resistencias
E_L=L*(i1^2+i2^2)/2; %autoinducción
i0=V0/(R+R3);
E_L0=i0^2*L/2; %inicial
s1=subs(E_V,{t, R, R3, L, V0},{100/1000,89,200,4,9.3});
s2=subs(E_R+E_L-E_L0,{t, R, R3, L, V0},{100/1000,89,200,4,9.3});
disp([double(s1),double(s2)])
Obteniendo los mismos resultados
Referencias
Carl E. Mungan. Double-Exponential LR circuit. The Physics Teacher, Vol. 43, November 2005, pp. 519-523

