Teniendo en cuenta las relaciones

${\displaystyle \begin{array}{l}{e}^{-i\omega t}=\cos \omega t-i\sin \omega t\\ e^{i\omega t}=\cos \omega t+i\sin \omega t\end{array}}$

El desarrollo en serie de Fourier para una función periódica de perido P

${\displaystyle f(t)=\frac{a_0}{2}+{\displaystyle \sum _{k=1}^{\infty }\left(a_k\cos \left(k\frac{2\pi }{P}t\right)+b_k\sin \left(k\frac{2\pi }{P}t\right)\right)}}$

se expresa de la siguiente forma alternativa

${\displaystyle \begin{array}{l}f(t)=\frac{a_0}{2}+{\displaystyle \sum _{k=1}^{\infty }\left(\frac{a_k}{2}\left(e^{ik2\pi t/P}+e^{-ik2\pi t/P}\right)+\frac{b_k}{2i}\left(e^{ik2\pi t/P}-e^{-ik2\pi t/P}\right)\right)}\\ c_0=\frac{a_0}{2}{c}_k=\frac{a_k-i{b}_k}{2}{c}_{-k}=\frac{a_k+i{b}_k}{2}\\ f(t)=c_0+{\displaystyle \sum _{k=1}^{\infty }\left(c_k{e}^{ik2\pi t/P}+c_{-k}{e}^{-ik2\pi t/P}\right)}\\ f(t)={\displaystyle \sum _{-\infty }^{\infty }{c}_k\exp \left(ik2\pi \frac{t}{P}\right)}{c}_k=\frac{1}{P}{\displaystyle \underset{-P/2}{\overset{P/2}{\int }}f(t)\exp \left(-ik2\pi \frac{t}{P}\right)dt}\end{array}}$

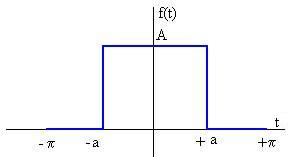
Pulso rectangular

${\displaystyle c_k=\frac{1}{2\pi }{\displaystyle {\int }_{-a}^{a}A{e}^{-ikt}dt=}\frac{A}{k\pi }\sin \left(ka\right)=\{\begin{array}{l}k=0c_0=\frac{A}{\pi }a\\ k\ne 0c_k=\frac{A}{k\pi }\sin \left(ka\right)\end{array}}$

>>syms k A a;
>> ck=int(A*exp(-i*k*t),t,-a,a)/(2*pi)
ck =(A*sin(a*k))/(pi*k)

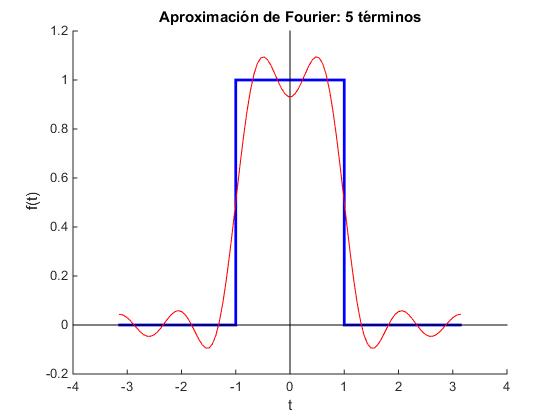
Dibujamos la función f(t) entre -π y +π en color azul y con ancho de línea 2 y la aproximación a la función sumando n términos del desarrollo en serie (positivos y negativos) en color rojo de anchura de línea 1. Tomamos A=1

a=1; %Semianchura del pulso rectangular a<pi
n=5; %Número de términos
hold on
x=[-pi -a -a a a pi];
y=[0 0 1 1 0 0];
plot(x,y,'b','linewidth',2)
x=linspace(-pi,pi,100);
y=zeros(length(x),1);
for j=1:length(x)
    y(j)=0;
    for k=-n:n
        if k==0 
            y(j)=y(j)+a/pi;
        else
            y(j)=y(j)+sin(k*a)*exp(i*k*x(j))/(k*pi);
        end
     end
end

%ejes
plot([-4 4],[0 0],'k')
plot([0 0],[-0.2 1.2],'k')
%serie de Fourier
plot(x,real(y),'r');
title(sprintf('Aproximación de Fourier: %i términos',n))
xlabel('t'); ylabel('f(t)')
hold off

Pulso diente de sierra

${\displaystyle c_k=\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }\frac{A}{\pi }t{e}^{-ikt}dt=}\frac{A}{k\pi }i\cos \left(k\pi \right)=\frac{A}{k\pi }{\left(-1\right)}^{k}i}$

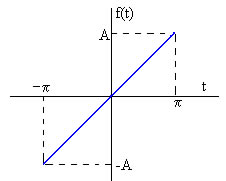
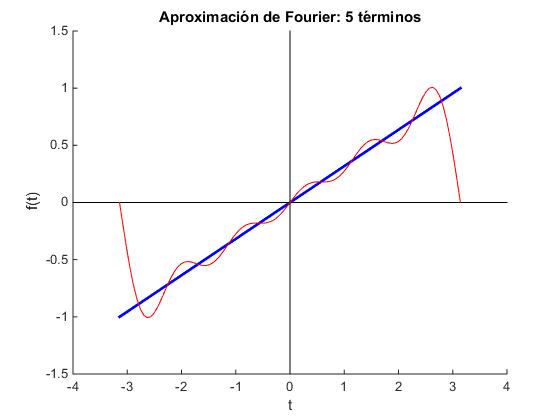
Dibujamos la función f(t) entre -π y +π en color azul y con ancho de línea 2, la aproximación a la función sumando n términos del desarrollo en serie (positivos y negativos) en color rojo de anchura de línea 1. Tomamos A=1

n=5; %Número de términos
hold on
plot([-pi,pi],[-1 1],'b','linewidth',2)
x=linspace(-pi,pi,100);
y=zeros(length(x),1);
for j=1:length(x)
    y(j)=0;
    for k=-n:n
        y(j)=y(j)+(-1)^k*1i*exp(1i*k*x(j))/(k*pi);
    end
end
%ejes
plot([-4 4],[0 0],'k')
plot([0 0],[-1.5 1.5],'k')
%serie de Fourier
plot(x,real(y), 'r');
title(sprintf('Aproximación de Fourier: %i términos',n))
xlabel('t'); ylabel('f(t)')
hold off