1. La ecuación diferencial del Movimiento Ondulatorio es

${\displaystyle c^2\frac{{\partial }^2\psi }{\partial x^2}=\frac{{\partial }^2\psi }{\partial t^2}}$

siendo c la velocidad de propagación de las ondas en la cuerda y ψ el desplazamiento trasversal de un punto x de la cuerda en el instante t.

2. Estudiamos una solución de la forma

ψ(x,t)=y(x)·sin(ωt)

Cada punto de la cuerda vibra con una amplitud y(x) y con frecuencia angular ω.

La ecuación diferencial se convierte en

${\displaystyle \frac{d^{2}y}{d{x}^2}+\frac{{\omega }^2}{c^2}y=0}$

La solución de esta ecuación diferencial, similar a la de un M.A.S., es

y=Asin (kx)+Bcos(kx)  con k=ω/c  que es el número de onda

3. Las condiciones de contorno son:

La cuerda está fija por sus extremos x=0 y x=l

De la primera condición, tenemos que B=0.

y de la segunda,

sin(kl)=0 ó bien, kl=nπ, con n=1, 2, 3,…

que nos da los distintas frecuencias de vibración de la cuerda

${\displaystyle f_n=\frac{{\omega }_n}{2\pi }=v\frac{n}{2l}n=\text{1}\text{, 2}\text{, 3}\text{, }\mathrm{...}}$

La amplitud de las oscilaciones de los puntos x de la cuerda en el modo normal n es

${\displaystyle y_n(x)=A\sin \left(\frac{n\pi }{l}x\right)}$

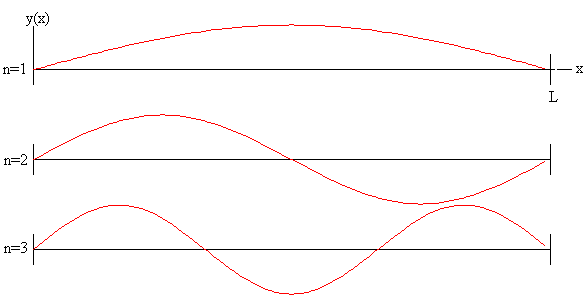
Estas funciones cumplen que

$$\begin{gathered} {\displaystyle {\displaystyle \underset{0}{\overset{l}{\int }}{y}_n^2(x)·dx}=\frac{A^2}{2}{\displaystyle \underset{0}{\overset{l}{\int }}\left(1-\text{cos}\left(\frac{2n\pi }{l}x\right)\right)}dx=\frac{A^2}{2}{\left(x-\frac{l}{2n\pi }\sin \left(\frac{2n\pi }{l}x\right)\right)}_0^l= \\ \frac{A^2}{2}l} \end{gathered}$$

La integral es el área bajo la curva de la figura inferior.

Actividades

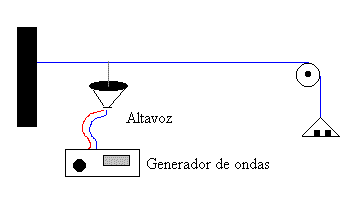
Una cuerda horizontal está sujeta por uno de sus extremos, del otro extremo cuelga un platillo en el que se ponen pesas. Una aguja está sujeta al centro de la membrana de un altavoz y por el otro extremo está sujeta a la cuerda. La aguja empieza a vibrar cuando se conecta el altavoz al generador de ondas .

Tenemos un sistema oscilante, la cuerda y la fuerza oscilante proporcionada por la aguja. Cuando la frecuencia de la fuerza oscilante, la que marca el generador coincide con alguno de los modos de vibración de la cuerda, la amplitud de su vibración se incrementa notablemente, estamos en una situación de resonancia

En la página titulada Modos de vibración forzados de una cuerda se describe la simulación de esta experiencia de laboratorio

Nuestra experiencia simulada, difiere de la experiencia en el laboratorio, en que no cambiamos directamente la tensión de la cuerda sino la velocidad de propagación de las ondas.

Una vez establecida la velocidad de propagación o la la tensión de la cuerda, vamos cambiando la frecuencia de la fuerza oscilante para buscar los distintos modos de oscilación de la cuerda.

Una vez que encontramos la frecuencia del primer modo de vibración, se pueden buscar rápidamente los restantes: la frecuencia del segundo modo es el doble que la del modo fundamental, la frecuencia del tercer modo es triple y así, sucesivamente...

• f₁ modo fundamental
• f_n=nf₁ armónicos n=2, 3, 4....

Se introduce

• la velocidad de propagación en el control titulado Velocidad.
• la frecuencia de la fuerza oscilante, en el control titulado Frecuencia (Hz)

Se pulsa en el botón titulado Nuevo.

Como ejercicio, el lector puede hallar los primeros modos de vibración de una cuerda cuando sus velocidades de propagación son sucesivamente 4, 8, etc.

Los nodos, puntos cuya amplitud de oscilación es nula, se señalan mediante flechas de color rojo.

Superposición de la onda incidente y reflejada

En este apartado, obtendremos de otra forma la fórmula que nos da las frecuencias de los modos de vibración de una cuerda de longitud L, sujeta por sus extremos.

Una onda estacionaria se puede considerar como la superposición de dos movimientos ondulatorios armónicos de la misma amplitud y longitud de onda:

• una incidente, que se propaga de izquierda a derecha

Ψ_i=A·sin(kx-ωt)

• y otra relejada, que se propaga de derecha a izquierda.

Ψ_r=A·sin(kx+ωt)

La onda estacionaria resultante es

Ψ =Ψ_i+Ψ_r=2A·sin(kx)·cos(ωt).

Como vemos esta expresión no corresponde a una onda de propagación, no tiene el término (kx-ωt), sino que cada punto de la cuerda vibra con una frecuencia angular ω y una amplitud 2A·sin(kx).

Se denominan nodos a los puntos x que tienen una amplitud nula, 2A·sin(kx)=0, por lo que kx=nπ con n=1, 2, 3, .... o bien, x=λ/2, λ, 3λ/2, ... La distancia entre dos nodos consecutivos es media longitud de onda, λ/2.

Considérese ahora una cuerda de longitud l fija en los extremos. La cuerda tiene un conjunto de modos normales de vibración, cada uno con una frecuencia característica. Las frecuencias se pueden calcular fácilmente.

En primer lugar, los extremos de la cuerda deben de ser nodos ya que estos puntos se encuentran fijos. El primer modo de vibración será aquél en el que la longitud de la cuerda sea igual a media longitud de onda l=λ/2. Para el segundo modo de vibración, la longitud de la cuerda será igual a una longitud de onda, l=λ. Para el tercer modo, l=3λ/2 y así, sucesivamente. En consecuencia, las longitudes de onda de los diferentes modos de vibración se puede expresar como

${\displaystyle {\lambda }_n=\frac{2l}{n}n=\mathrm{1,2,3,...}}$

Para hallar las frecuencias empleamos la relación λ =vP, o bien λ =v/f .

${\displaystyle f_n=\frac{n}{2l}v}$

Actividades

Se introduce

• La frecuencia f del movimiento ondulatorio armónico, en el control de edición titulado Frecuencia.
• La velocidad de propagación se ha fijado en la unidad v=1. De modo, que la longitud de onda λ=1/f

Se pulsa en el botón titulado Nuevo

Se observa que:

1. Una onda estacionaria (en color negro) se origina por la superposición de dos movimientos ondulatorios armónicos de la misma frecuencia que se mueven en direcciones opuestas, uno incidente (de color rojo) y otro reflejado (de color azul claro) .
2. Cuando la onda incidente se refleja en el origen x=0 experimenta un cambio de fase de π.