Una función es periódica de periodo P si hay un número P>0 tal que f(t+P)=f(t). Cualquier múltiplo n entero de P es también periodo f(t+nP)=f(t)

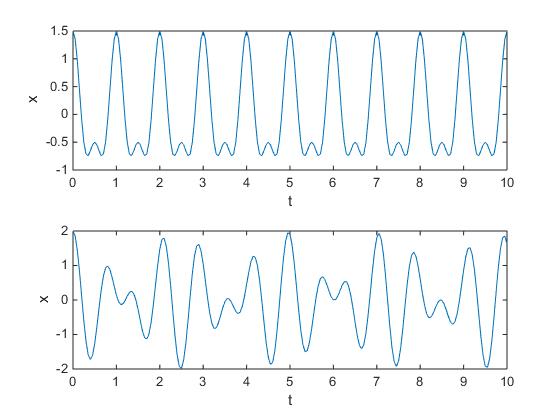
La función f(t)=cos(2πt)+cos(4πt)/2, es la suma de dos funciones periódicas de periodos 1 y 0.5, respectivamente. Como vemos en la gráfica f(t) es periódica con periodo P=1.

Las funciones cos(t) y $\cos \left(\sqrt{2}t\right)$ son periódicas de periodo 2π y $2\pi /\sqrt{2}$ respectivamente, pero la suma

${\displaystyle f(t)=\cos \left(t\right)+\cos \left(\sqrt{2}t\right)}$

no es periódica.

t=0:0.05:10;
x=cos(2*pi*t)+cos(4*pi*t)/2;
subplot(2,1,1)
plot(t,x);
xlabel('t')
ylabel('x')

subplot(2,1,2)
x=cos(2*pi*t)+cos(2*pi*sqrt(2)*t);
plot(t,x);
xlabel('t')
ylabel('x')

Superposición de funciones armónicas

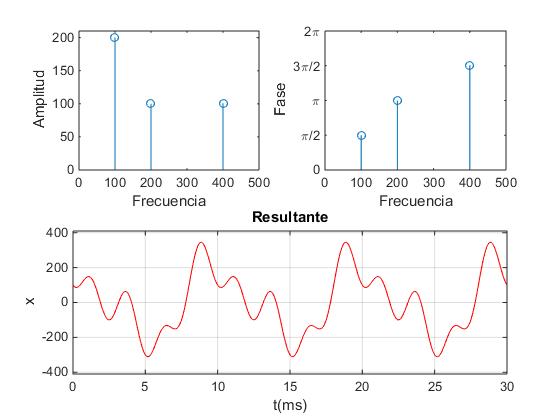
Sea una función periódica resultado de la superposición de tres funciones armónicas con distintas frecuencias, amplitudes y fases iniciales

x=200sin(2π·100+π/2)+100sin(2π·200+π)+100sin(2π·400+3π/2)

f=[100,200,400]; %frecuencias
A=[200,100,100]; %amplitudes
phi=[90,180,270]; %fases

subplot(2,2,1)
stem(f,A)
axis([0,500,0,210])
xlabel('Frecuencia')
ylabel('Amplitud')

subplot(2,2,2)
stem(f,phi)
axis([0,500,0,360])
xlabel('Frecuencia')
set(gca,'YTick',0:90:360)
set(gca,'YTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
ylabel('Fase')

subplot(2,2,3:4) %resultante
t=(0:0.1:30)/1000; %milisegundos
x=zeros(1,length(t));
for i=1:length(f)
    x=x+A(i)*sin(2*pi*f(i)*t+phi(i)*pi/180);
end
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
title('Resultante')
ylim([-410,410])
set(gca,'XTick',(0:5:30)/1000)
set(gca,'XTickLabel',{'0','5','10','15','20','25','30'})
grid on

Serie de Fourier

Una función f(t) periódica de periodo P, se puede representar en forma de una suma infinita de funciones armónicas es decir,

${\displaystyle f(t)=\frac{a_0}{2}+{\displaystyle \sum _{k=1}^{\infty }\left(a_k\cos \left(k\frac{2\pi }{P}t\right)+b_k\sin \left(k\frac{2\pi }{P}t\right)\right)}}$

donde a₀ a₁ ...a_k ... y b₁ b₂ .... b_k .... son los denominados coeficientes de Fourier.

Teniendo en cuenta los resultados de las integrales

${\displaystyle \underset{-P/2}{\overset{P/2}{\int }}\cos \left(m\frac{2\pi }{P}t\right)\sin \left(n\frac{2\pi }{P}t\right)}dt=\frac{P}{2\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\cos \left(mx\right)\sin \left(nx\right)dx}=0$

>> syms m n t;
>> y=int('sin(m*t)*cos(n*t)',t,-pi,pi)
y =0

${\displaystyle \underset{-P/2}{\overset{P/2}{\int }}\cos \left(m\frac{2\pi }{P}t\right)\cos \left(n\frac{2\pi }{P}t\right)}dt=\frac{P}{2\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\cos \left(mx\right)\cos \left(nx\right)dx}=\{\begin{array}{l}0m\ne n\\ \frac{P}{2}m=n\end{array}$

>> syms m n t;
>> y=int('cos(m*t)*cos(n*t)',t,-pi,pi);
>> assume(m,'integer')
>> assume(n,'integer')
>> assume(m==n)
>> simplify(y)
ans =pi

${\displaystyle \underset{-P/2}{\overset{P/2}{\int }}\sin \left(m\frac{2\pi }{P}t\right)\sin \left(n\frac{2\pi }{P}t\right)}dt=\frac{P}{2\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\sin \left(mx\right)\sin \left(nx\right)dx}=\{\begin{array}{l}0m\ne n\\ \frac{P}{2}m=n\end{array}$

Los coeficientes del desarrollo en serie valen

${\displaystyle \begin{array}{l}{a}_k=\frac{2}{P}{\displaystyle \underset{-P/2}{\overset{P/2}{\int }}f(t)\cos \left(k\frac{2\pi }{P}t\right)}dtk=\mathrm{0,1,2,3...}\\ b_k=\frac{2}{P}{\displaystyle \underset{-P/2}{\overset{P/2}{\int }}f(t)\sin \left(k\frac{2\pi }{P}t\right)}dtk=\mathrm{1,2,3...}\end{array}}$

La suma parcial de las series de Fourier es

${\displaystyle s_n(t)=\frac{a_0}{2}+{\displaystyle \sum _{k=1}^n\left(a_k\cos \left(k\frac{2\pi }{P}t\right)+b_k\sin \left(k\frac{2\pi }{P}t\right)\right)}}$

Si la función f(t) tiene simetría, algunos de los coeficientes resultan nulos.

• Si f(t) es una función par, f(t)=f(-t), los términos b_k son nulos
• Si f(t) es impar f(t)=-f(-t), los coeficientes a_k son nulos

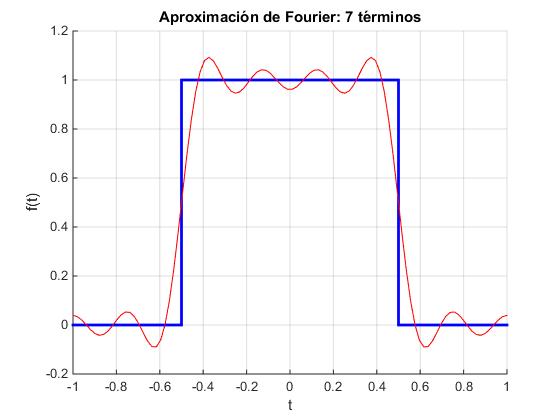
Función par

Por ejemplo, para el pulso rectangular simétrico de anchura 1 y periodo P=2 se obtienen los siguientes coeficientes.

${\displaystyle \begin{array}{l}{a}_0=\frac{2}{2}{\displaystyle \underset{-0.5}{\overset{0.5}{\int }}dt}=1\\ a_k=\frac{2}{2}{\displaystyle \underset{-0.5}{\overset{0.5}{\int }}\cos \left(k\pi t\right)dt=}\frac{2}{k\pi }\left(\sin \left(\frac{k\pi }{2}\right)\right)\{\begin{array}{l}0k\text{par}\\ \frac{2}{k\pi }{\left(-1\right)}^{(k-1)/2}k\text{impar}\end{array}\end{array}}$

>> syms t P k;
>> ak=int(cos(pi*k*t),t,-0.5,0.5);
>> subs(ak,k,sym('[1 2 3 4 5 6 7]'))
ans =[ 2/pi, 0, -2/(3*pi), 0, 2/(5*pi), 0, -2/(7*pi)]

Vamos a reconstruir la función f(t) a partir del desarrollo en serie de Fourier.

${\displaystyle s_n(t)=\frac{1}{2}+\frac{2\cos (\pi t)}{\pi }-\frac{2\cos (3\pi t)}{3\pi }+\frac{2\cos (5\pi t)}{5\pi }-\frac{2\cos (7\pi t)}{7\pi }+\mathrm{...}}$

n=7; %número de términos
hold on
x=[-1 -0.5 -0.5 0.5 0.5 1];
y=[0 0 1 1 0 0];
plot(x,y,'b','linewidth',2)
x=linspace(-1,1,100);
y=zeros(length(x),1);
for i=1:length(x)
    y(i)=1/2;
    for k=1:2:n
        y(i)=y(i)+(-1)^((k-1)/2)*2*cos(k*pi*x(i))/(k*pi);
     end
end
plot(x,y, 'r');
title(sprintf('Aproximación de Fourier: %i términos',n))
xlabel('t'); 
ylabel('f(t)')
grid on
hold off

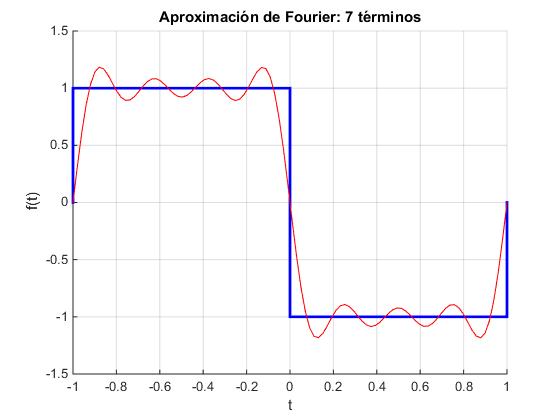
Función impar

Sea ahora la función de periodo P=2

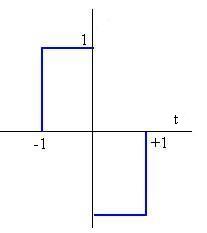
Es una función impar, los coeficientes a_k son nulos

${\displaystyle b_k={\displaystyle \underset{-1}{\overset{0}{\int }}\sin \left(k\pi t\right)dt}-{\displaystyle \underset{0}{\overset{1}{\int }}\sin \left(k\pi t\right)dt}=\frac{1}{k\pi }\left(-2+2\cos (k\pi )\right)=\{\begin{array}{l}0k\text{par}\\ \frac{-4}{k\pi }k\text{impar}\end{array}}$

>> syms t P k;
>> bk=int(sin(pi*k*t),t,-1,0)-int(sin(pi*k*t),t,0,1);
>> subs(bk,k,sym('[1 2 3 4 5 6 7]'))
ans =[ -4/pi, 0, -4/(3*pi), 0, -4/(5*pi), 0, -4/(7*pi)]

El desarrollo en serie es

${\displaystyle s_n(t)=-\frac{4\sin (\pi t)}{\pi }-\frac{4\sin (3\pi t)}{3\pi }-\frac{4\sin (5\pi t)}{5\pi }-\frac{4\sin (7\pi t)}{7\pi }+\mathrm{...}}$

n=7; %Número de términos;
hold on
x=[-1 -1 0 0 1 1];
y=[0 1 1 -1 -1 0];
plot(x,y,'b','linewidth',2)
x=linspace(-1,1,100);
y=zeros(length(x),1);
for i=1:length(x)
    y(i)=0;
    for k=1:2:n
        y(i)=y(i)-4*sin(k*pi*x(i))/(k*pi);
     end
end
plot(x,y, 'r');
title(sprintf('Aproximación de Fourier: %i términos',n))
xlabel('t'); 
ylabel('f(t)')
grid on
hold off