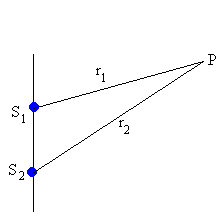
Consideremos dos fuentes puntuales S₁ y S₂ que oscilan en fase con la misma frecuencia angular ω, y que emiten ondas armónicas.

Cuando emite solamente S₁ el punto P describe el Movimiento Armónico Simple (M.A.S.) de amplitud A₁ y frecuencia angular ω .

Ψ₁=A₁·sin(kr₁-ωt)

Cuando emite solamente S₂ el punto P describe el M.A.S. de amplitud A₂ y frecuencia angular ω.

Ψ₂=A₂·sin(kr₂-ωt)

Cuando emiten simultáneamente S₁ y S₂. El punto P describe un M.A.S. que es la composición de dos M.A.S. de la misma dirección y frecuencia. Los casos más importantes son aquellos en los que los M.A.S. están en fase y en oposición de fase.

En fase o interferencia constructiva.

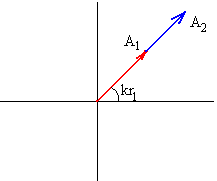
Dos M.A.S están en fase cuando la diferencia de fase δ=kr₂-kr₁ es un múltiplo entero de 2π .Teniendo en cuenta que k=2π /λ

kr₂-kr₁ =2nπ     r₂-r₁ =nλ

La amplitud resultante es la suma de amplitudes A=A₁+A₂

En oposición de fase o interferencia destructiva.

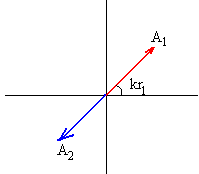
Dos M.A.S están en oposición de fase cuando la diferencia de fase δ=kr₂-kr₁ es un múltiplo entero de π .Teniendo en cuenta que k=2π /λ

kr₂-kr₁ =(2n+1)π     r₂-r₁ =(n+½)λ

La amplitud resultante es la diferencia de amplitudes. Si ambas son iguales, el punto P no se mueve.

Amplitud resultante

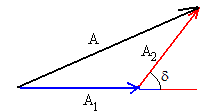
En el caso general, es necesario sumar vectorialmente las amplitudes para obtener la resultante.

${\displaystyle A=\sqrt{A_1^2+A_2^2+2A_1{A}_2\cos (k{r}_2-k{r}_1)}}$

• La amplitud es máxima A=A₁+A₂ cuando δ=kr₂-kr₁=2nπ
• La amplitud es mínima A=A₁-A₂ cuando δ=kr₂-kr₁=(2n+1)π

Si la separación d de las fuentes S₁ y S₂ es pequeña comparada con la distancia desde las fuentes hasta la pantalla, podemos despreciar la pequeña diferencia entre r₁ y r₂ y suponer que las amplitudes A₁ y A₂ son prácticamente iguales.

${\displaystyle A=2A_1\cos \frac{k(r_2-r_1)}{2}}$

Máximos y mínimos de intensidad

En la figura, vemos la amplitud debida a la interferencia de las ondas emitidas por dos fuentes sincrónicas separadas una distancia d, tal como se vería en una cubeta de ondas cuando nos situamos cerca de las fuentes.

En la figura, vemos la intensidad debida a la interferencia de las ondas producidas por dos fuentes sincrónicas separadas una distancia d, codificada en escala de grises. El color negro indica mínimo de intensidad y el color blanco máximo de intensidad.

Las curvas que describen los máximos (en color azul) y mínimos (en color rojo) de intensidad es el lugar geométrico de los puntos (x, y) cuya ecuación y=f(x) vamos a determinar

El lugar geométrico de los puntos cuya diferencia de caminos es Δ es r₂-r₁=Δ.

r₂ es la distancia de la fuente S₂ al punto P y r₁ es la distancia de la fuente S₁ al punto P.

• Δ=nλ, si la interferencia es constructiva (máximo de intensidad)
• Δ=(2n+1)λ/2, si la interferencia es destructiva (mínimo de intensidad)

Si las coordenadas del punto P son (x, y), y (0, ±d/2) son las posiciones de las fuentes, la ecuación de la curva r₂-r₁=Δ. es

${\displaystyle \sqrt{x^2+{\left(y+\frac{d}{2}\right)}^2}=\Delta +\sqrt{x^2+{\left(y-\frac{d}{2}\right)}^2}}$

Elevando al cuadrado ambos miembros para eliminar la raíz cuadrada

${\displaystyle 2yd-{\Delta }^2=2\Delta \sqrt{x^2+{\left(y-\frac{d}{2}\right)}^2}}$

Elevando al cuadrado ambos miembros otra vez, obtenemos

${\displaystyle \frac{4y^2}{{\Delta }^2}-\frac{4x^2}{d^2-{\Delta }^2}=1}$

que es la ecuación de una hipérbola

Si la pantalla se encuentra a una distancia x de las fuentes. Las posiciones de los máximos y los mínimos se calculan despejando y de la ecuación de la hipérbola

${\displaystyle y=\pm \frac{\Delta }{2}\sqrt{1+\frac{4x^2}{d^2-{\Delta }^2}}}$

• El primer máximo, se produce cuando Δ=0, y=0
• El primer mínimo, se produce cuando Δ=λ/2,
• El segundo máximo, se produce cuando Δ=λ
• El segundo mínimo, se produce cuando Δ=3λ/2

y así, sucesivamente.

En la figura, vemos los frentes de onda circulares separados una longitud de onda λ emitidos por dos fuentes S₁ y S₂ y las parábolas correspondientes a los máximos de intensidad Δ=λ, 2λ, 3λ y sus simétricas

lambda=2; %longitud de onda
d=10; %separación entre las dos fuentes
hold on
for k=1:9
    fplot(@(t) k*lambda*cos(t), @(t) d/2+k*lambda*sin(t),[0,2*pi],
'lineWidth',0.5,'color','k')
    fplot(@(t) k*lambda*cos(t), @(t) -d/2+k*lambda*sin(t),[0,2*pi],
'lineWidth',0.5,'color','k')
end
for Delta=(0:5)*lambda %máximos
    fplot(@(x) Delta*sqrt(1+4*x.^2/(d^2-Delta^2))/2,[0,10*lambda],'r')
    fplot(@(x) -Delta*sqrt(1+4*x.^2/(d^2-Delta^2))/2,[0,10*lambda],'r')
end
plot(0,d/2,'ro','markersize',3,'markerfacecolor','r') %fuentes
plot(0,-d/2,'ro','markersize',3,'markerfacecolor','r')
hold off
axis equal
xlim([-lambda, 10*lambda])

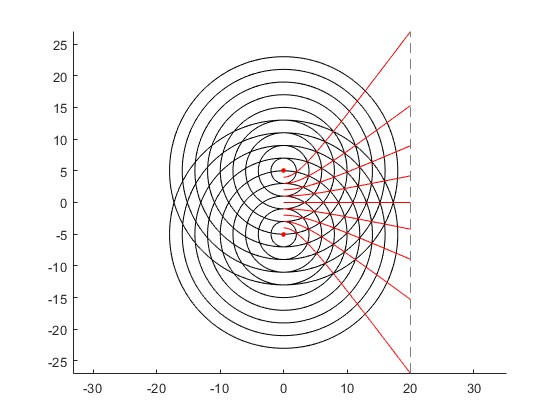
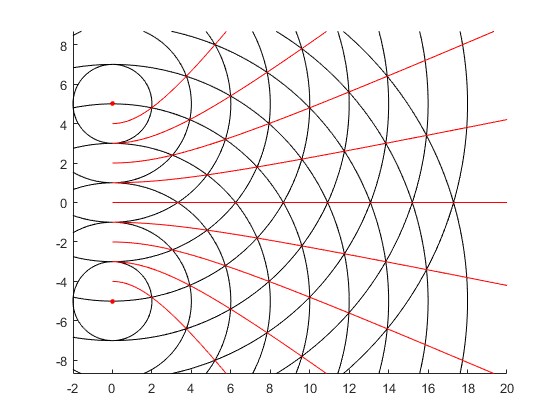
La hipérbola se aproxima a una recta, su asíntota, cuando nos alejamos una distancia no demasiado grande de las fuentes.

Despejamos el cociente y/x en la ecuación de la hipérbola

${\displaystyle \frac{y}{x}=\frac{\Delta }{2}\sqrt{\frac{1}{x^2}+\frac{4}{d^2-{\Delta }^2}}}$

La pendiente de la asíntota se calcula en el límite cuando x→∞

${\displaystyle \tan \theta =\underset{x\to \infty }{\lim }\left(\frac{y}{x}\right)=\frac{\Delta }{2}\underset{x\to \infty }{\lim }\sqrt{\frac{1}{x^2}+\frac{4}{d^2-{\Delta }^2}}=\frac{\Delta }{\sqrt{d^2-{\Delta }^2}}}$

Empleando la relación trigonométrica

${\displaystyle {\sin }^2\theta =\frac{{\tan }^2\theta }{1+{\tan }^2\theta }\sin \theta =\frac{\Delta }{d}}$

Con esta aproximación, la diferencia de caminos r₂-r₁=Δ≈d·sinθ, tal como apreciamos en la figura. Esta última relación, nos permite determinar las direcciones θ para las cuales la interferencia es constructiva o destructiva.

• El primer máximo, se produce cuando Δ=0, para el ángulo θ=0
• El primer mínimo, se produce cuando Δ=λ/2, para el ángulo d·sinθ= λ/2
• El segundo máximo, se produce para Δ=λ, para el ángulo d·sinθ= λ
• El segundo mínimo, se produce para Δ=3λ/2, para el ángulo d·sinθ= 3λ/2

Si la pantalla está a una distancia x de las fuentes, la posición y de los máximos y mínimos de intensidad se calcula mediante al relación

y=x·tanθ

En la mayor parte de los experimentos, incluso en la cubeta de ondas es difícil apreciar la parte curva de las hipérbolas, lo comprobaremos al final de la página en la simulación de la cubeta de ondas. En un experimento de óptica, la distancia entre las fuentes d=2·10^-4 m, la longitud de onda λ=6·10^-7 m y la distancia a la pantalla x=2 m.

Ejemplo

• La separación entre las fuentes es d=100
• La longitud de onda es λ=50

1. La posición de la pantalla se encuentra en x=100

Determinar las posiciones y de los máximos y mínimos de intensidad a lo largo de la pantalla. Utilizamos la fórmula

${\displaystyle y=\pm \frac{\Delta }{2}\sqrt{1+\frac{4x^2}{d^2-{\Delta }^2}}}$

• El primer máximo, se produce cuando Δ=0, y=0
• El primer mínimo, se produce cuando Δ=λ/2=25, y=28.7
• El segundo máximo, se produce cuando Δ=λ=50, y=62.9
• El segundo mínimo, se produce cuando Δ=3λ/2=75, y=119.4

2. La posición de la pantalla se encuentra en x=200

• El primer máximo, se produce cuando Δ=0, y=0
• El primer mínimo, se produce cuando Δ=λ/2=25, y=53.1
• El segundo máximo, se produce cuando Δ=λ=50, y=118.1

Calculamos las direcciones mediante la fórmula d·sinθ=Δ y las posiciones mediante la expresión, y=x·tanθ

• El primer máximo, se produce cuando Δ=0, θ=0, y=0
• El primer mínimo, se produce cuando Δ=λ/2=25, θ=14.5º, y=51.6
• El segundo máximo, se produce cuando Δ=λ=50, θ=30º, y=115.5

Como vemos, aunque la pantalla sigue estando cerca de las fuentes, la aproximación d·sinθ=Δ, da buenos resultados.

Condiciones de interferencia: constructiva, destructiva

Las condiciones de interferencia son:

• Interferencia constructiva, r₂-r₁=nλ .
• Interferencia destructiva, r₂-r₁=(n+½)λ

Las direcciones θ para las cuales la interferencia es constructiva o destructiva se calculan

• Interferencia constructiva, d·sinθ ≈nλ .
• Interferencia es destructiva, d·sinθ ≈(n+½)λ

Las posiciones y sobre la pantalla situada a una distancia x de las fuentes, que registran interferencia constructiva y destructiva se calculan mediante y=x·tanθ .

Si el ángulo θ es pequeño, hacemos la aproximación, sinθ ≈tanθ =y/x

La intensidad de un movimiento ondulatorio es proporcional al cuadrado de la amplitud,

${\displaystyle \begin{array}{l}A=2A_1\cos \frac{k(r_2-r_1)}{2}=2A_1\cos \left(\frac{\pi d}{\lambda }\sin \theta \right)\\ I=4I_0{\cos }^2\left(\frac{\pi d}{\lambda }\sin \theta \right)\end{array}}$

I es la intensidad resultante en el punto P cuando las dos fuentes emiten simultáneamente, e I₀ es la intensidad en el punto P debido a una sola de las fuentes.

• En la interferencia constructiva, d·sinθ =nλ la intensidad I=2²I₀.
• En la interferencia destructiva, d·sinθ =(n+½)λ y la intensidad I=0.

En la figura, se muestra la gráfica de la intensidad, el máximo es 4I₀. y el mínimo 0.

Actividades

Se introduce

• La longitud de onda λ, en el control titulado Longitud onda
• La separación d, entre las dos fuentes, en el control titulado Separación .

Se pulsa el botón titulado Nuevo

Se muestra, a la izquierda, el diagrama de amplitudes resultado de la interferencia de las ondas producidas por las dos fuentes sincrónicas. Esta figura es similar a la que se puede observar en el laboratorio cuando se realiza una experiencia con la cubeta de ondas.

A la derecha, el diagrama de intensidades. La intensidad en cada punto se codifica mediante un color perteneciente a la escala de grises. La intensidad máxima corresponde al blanco y la mínima al color negro.

Se activa la casilla titulada Regla y se pulsa el botón titulado Nuevo

Se superpone sobre el diagrama de intensidades, la representación gráfica de las hipérbolas que describen el lugar geométrico de los puntos P tal que la diferencia de caminos r₂-r₁ de las fuentes S₂ y S₁ al punto P es un múltiplo entero de la longitud de onda nλ (en color azul) o de los puntos cuya diferencia de caminos es un múltiplo semientero de la longitud de onda (n+½)λ (en color rojo).

Cambiamos la posición de la regla vertical en el control titulado Pantalla acercándola o alejándola de las fuentes.

Para una posición x, se puede medir mediante la regla vertical, las posiciones de los máximos y mínimos de intensidad a lo largo de la pantalla.

El espejo de Lloyd

Una fuente S emite ondas de longitud de onda λ. En un punto P de la pantalla situada a una distancia d de la fuente se observa la interferencia de de las ondas que llegan directamente a P y de las que se reflejan en un espejo de longitud l.

Como vemos en la figura, tenemos en P la interferencia de las ondas producidas por una fuente S y su imagen S', que vibran con la misma frecuencia y en fase

La diferencia de caminos Δ=(SMP)-(SP)=(S'P)-(SP)=r₂-r₁. Como apreciamos en la figura

${\displaystyle \begin{array}{l}\Delta \approx 2h\sin \theta \\ \tan \theta =\frac{x}{d}\approx \sin \theta \\ \Delta \approx 2\frac{h}{d}x\end{array}}$

De otra forma, utilizando la aproximación, $\sqrt{1+x}\approx 1+\frac{x}{2}$

>> syms x;
>> taylor(sqrt(1+x),x)
ans =(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 1

${\displaystyle \begin{array}{l}{r}_1=\sqrt{d^2+{\left(h-x\right)}^2}=d\sqrt{1+\frac{{\left(h-x\right)}^2}{d^2}}\approx d\left(1+\frac{1}{2}\frac{{\left(h-x\right)}^2}{d^2}\right)\\ r_2=\sqrt{d^2+{\left(h+x\right)}^2}=d\sqrt{1+\frac{{\left(h+x\right)}^2}{d^2}}\approx d\left(1+\frac{1}{2}\frac{{\left(h+x\right)}^2}{d^2}\right)\\ \Delta =r_2-r_1\approx \frac{1}{2}\frac{{\left(h+x\right)}^2-{\left(h-x\right)}^2}{d}=2\frac{h}{d}x\end{array}}$

Teniendo en cuenta que el rayos que se refleja en el espejo, experimentan un cambio de fase π, la diferencia de fase, de los dos rayos que llegan a P es

${\displaystyle \delta =k\Delta +\pi =\frac{2\pi }{\lambda }\Delta +\pi =2\pi \left(\frac{2h}{\lambda d}x+\frac{1}{2}\right)}$

La amplitud resultante en P es

${\displaystyle A=\sqrt{A_1^2+A_2^2+2A_1{A}_2\cos \delta }}$

• La interferencia es constructiva (amplitud máxima) cuando cosδ=1, δ=2nπ

• es destructiva cuando cosδ=-1, δ=(2n+1)π, con n=0, 1,2,3,...

Si la separación d de las fuentes S y S' es pequeña comparada con la distancia d desde las fuentes hasta la pantalla, podemos despreciar la pequeña diferencia entre r₁ y r₂ y suponer que las amplitudes A₁ y A₂ son prácticamente iguales.

${\displaystyle A\approx 2A_1\cos \left(\frac{\delta }{2}\right)}$

La intensidad es proporcional al cuadrado de la amplitud

${\displaystyle I\approx 4I_0{\cos }^2\left(\frac{\delta }{2}\right)=2I_0\left(1+\cos \delta \right)}$

• Interferencia constructiva, I=4I₀, intensidad máxima

La posición del centro de las franjas brillantes es

${\displaystyle \begin{array}{l}\delta =2n\pi \\ 2\pi \left(\frac{2h}{\lambda d}{x}_b+\frac{1}{2}\right)=2n\pi \\ x_b=\left(n-\frac{1}{2}\right)\frac{\lambda d}{2h}\end{array}}$

• Interferencia destructiva, I=0, intensidad mínima

La posición del centro de las franjas oscuras es

${\displaystyle \begin{array}{l}\delta =\left(2n+1\right)\pi \\ 2\pi \left(\frac{2h}{\lambda d}{x}_o+\frac{1}{2}\right)=\left(2n+1\right)\pi \\ x_0=n\frac{\lambda d}{2h}\end{array}}$

x_m es la distancia máxima a lo largo de la pantalla en la que se produce interferencia

${\displaystyle \begin{array}{l}\tan \alpha =\frac{h}{d-l}\\ x_m=l\tan \alpha =\frac{hl}{d-l}\end{array}}$

Ejemplo

• Distancia entre las fuente y las pantalla, d=80 cm
• Distancia entre la fuente y el espejo, h=1.5 mm
• Longitud del espejo, l=30 cm
• Longitud de onda, λ=0.6·10^-6 m

La posición de la quinta franja brillante, n=5 es x_b=0.72 mm

El número de franjas brillantes que hay en el intervalo es 0<x_b<x_m es

${\displaystyle \left(n-\frac{1}{2}\right)\frac{\lambda d}{2h}<\frac{hl}{d-l}}$

Obtenemos n<6.1250. Es decir, 6 franjas brillantes