Movimiento ondulatorio armónico

En la página web titulada "Descripción de la propagación" vemos en una animación la propagación de un pulso, cuya forma inicial viene descrito por la función f(x), a lo largo del eje X hacia la derecha con velocidad v y sin distorsionarse (sin cambiar de forma).

Ψ =f(x-vt) describe la propagación de una perturbación representada por la función f(x), sin distorsión, a la largo del eje X, hacia la derecha, con velocidad v.

${\displaystyle \frac{{\partial }^2\Psi }{\partial t^2}=v^2\frac{{\partial }^2\Psi }{\partial x^2}}$

Estudiamos un caso particular importante, aquél en el que la función f(x) es una función armónica (seno o coseno).

Ψ(x,t)=Ψ₀·sin k(x-vt)

Las características de esta función de dos variables, son las siguientes:

1. La función seno es periódica y se repite cuando el argumento se incrementa en 2π . La función Ψ(x, t) se repite cuando x se incrementa en 2π/k.

${\displaystyle k\left(x+\frac{2\pi }{k}-vt\right)=kx-kvt+2\pi }$

Se trata de una función periódica, de periodo espacial o longitud de onda λ =2π/k. La magnitud k se denomina número de onda.

2. Cuando se propaga un movimiento ondulatorio armónico, un punto x del medio describe un Movimiento Armónico Simple de amplitud Ψ₀ y frecuencia angular ω =kv.

Ψ(x,t)=Ψ₀·sin (kx-ω t)

El periodo de la oscilación es P=2π/ω y la frecuencia  f =1/P.

3. La igualdad ω =kv, nos permite relacionar el periodo espacial o longitud de onda λ y el periodo de la oscilación P de un punto del medio.

${\displaystyle \omega =kv\frac{2\pi }{P}=\frac{2\pi }{\lambda }v\lambda =vP}$

La longitud de onda λ está relacionada con la frecuencia f de la forma λ=v/f. Para una velocidad de propagación v, cuanto mayor es la longitud de onda menor es la frecuencia y viceversa.

x=-6:0.05:6;
k=2*pi/2;
w=2*pi/1;

for i=1:5
    subplot(5,1,i)
    t=(i-1)/4;
    y=sin(k*x-w*t);
    plot(x,y,'r');
    grid on
    ylim([-1.1,1.1])
    str=sprintf('t=%1.2f',t);
    title(str)
end

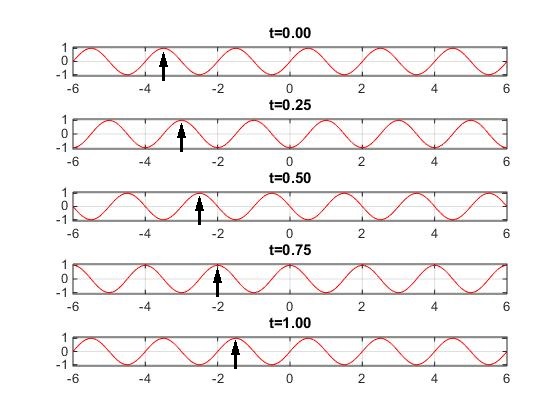
En la figura vemos que la longitud de onda es λ=2. Un punto del medio, por ejemplo x=0, describe un MAS cuyo periodo es P=1. Un pico (señalado con una flecha) se desplaza una longitud de onda durante un periodo de oscilación.

Superposición de ondas armónicas

Superponemos dos ondas armónicas de la misma amplitud A, la primera onda se propaga con velocidad v₁=ω₁/k₁ y la segunda con velocidad v₂=ω₂/k₂

${\displaystyle \begin{array}{l}{\Psi }_1(x,t)=A\sin (k_{1}x-{\omega }_{1}t)\\ {\Psi }_2(x,t)=A\sin (k_{2}x-{\omega }_{2}t)\\ {\Psi }_1(x,t)+{\Psi }_2(x,t)=2A\cos \left(\frac{k_1-k_2}{2}x-\frac{{\omega }_1-{\omega }_2}{2}t\right)\sin \left(\frac{k_1+k_2}{2}x-\frac{{\omega }_1+{\omega }_2}{2}t\right)\end{array}}$

Supongamos que k₁ y k₂ son números de onda cercanos, por ejemplo k₁=12 y k₂=10. Una fotografía de la onda resultante en el instante t=0, sería la siguiente

k1=12;
k2=10;
x=0:0.01:6;
y=2*cos((k1-k2)*x/2).*sin((k1+k2)*x/2); %superposición de dos ondas armónicas
y1=2*cos((k1-k2)*x/2); %envolvente
plot(x,y,'b',x,y1,'r',x,-y1,'r');
ylim([-2.1,2.1])
xlabel('x');
ylabel('y')
title('Superposición de ondas')
grid on

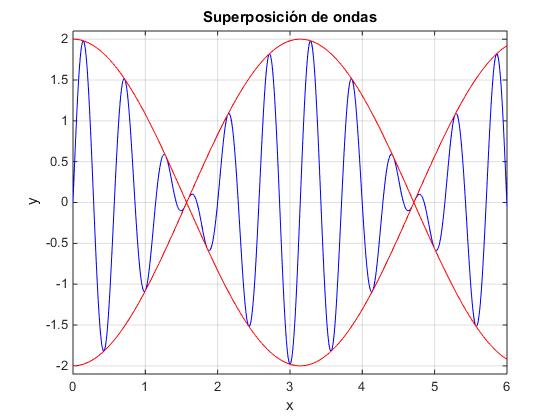
La curva en color rojo es la envolvente que varía como 2·cos(x) y la curva en color azul la superposición de las dos ondas en el instante t=0, que varía como 2·cos(x)·sin(11x). Dado que k₁≈ k₂ y ω₁≈ ω₂ la velocidad de la superposición (en color azul) de las dos ondas es v=ω₁/k₁≈ ω₂/k₂ y se denomina velocidad de fase. Sin embargo, la velocidad de la envolvente es Δω/Δk=(ω₁- ω₂)/(k₁-k₂ ), se denomina velocidad de grupo.

Las definiciones de velocidad de fase v_p y de grupo v_g son, respectivamente

${\displaystyle v_p=\frac{\omega }{k}{v}_g=\frac{d\omega }{dk}}$

Ambas velocidades son funciones de k y son distintas, en general.

fichero = 'onda_1.gif';
hg=figure;
set(hg,'Position',[0,0,568,180]) %posición y tamaño de la ventana gráfica
k1=12; w1=21;
k2=10; w2=20;
x=0:0.02:20;
for t=0:0.05:2*pi
    %superposición de dos ondas armónicas
    y=2*cos((k1-k2)*x/2-(w1-w2)*t/2).*sin((k1+k2)*x/2-(w1+w2)*t/2);
    y1=2*cos((k1-k2)*x/2-(w1-w2)*t/2); %envolvente
    plot(x,y,'b',x,y1,'r',x,-y1,'r');
    ylim([-2.1,2.1])
    xlabel('x');
    ylabel('y')
    title('Superposición de dos ondas')
   
    %GIF animado
    frame=getframe;
    im = frame2im(frame);
    [imind,cm] = rgb2ind(im,256);
    if t==0
        imwrite(imind,cm,fichero,'gif','DelayTime',0,'loopcount',inf);
    else
        imwrite(imind,cm,fichero,'gif','DelayTime',0,'writemode','append');
    end
end

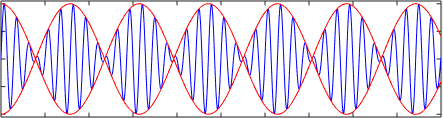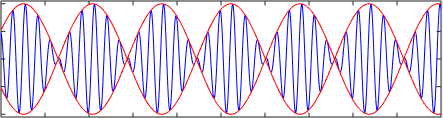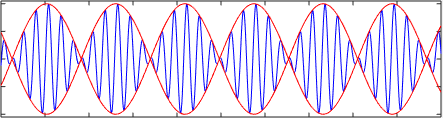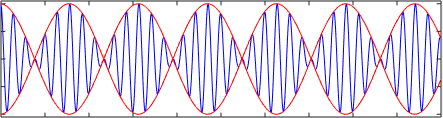
En esta animación, comparamos la velocidad de la envolvente (ω₁- ω₂)/(k₁-k₂ )=1/2 (en color rojo) con la velocidad de fase de las ondas (ω₁+ω₂)/(k₁+k₂ )=(21+20)/(12+10)≈2 (en color azul)

Ejemplos de medios dispersivos y no dispersivos

• Pequeñas ondas en la superficie del agua

${\displaystyle \omega =\sqrt{\frac{\sigma }{\rho }{k}^3}}$

donde σ es la tensión superficial del líquido y ρ su densidad

• Olas en aguas profundas

${\displaystyle \omega =\sqrt{gk}}$

• Olas de longitud de onda mucho mayor que la profundidad

${\displaystyle \omega =\sqrt{gH}k}$

donde H es la profundidad, se trata de un medio no dispersivo la velocidad de fase y de grupo coinciden

• Propagación de ondas en un plasma

${\displaystyle {\omega }^2={\omega }_{pe}^2\left(1+3k^2{\lambda }_D^2\right)}$

Velocidad de grupo

La ecuación de una onda armónica es

${\displaystyle \Psi (x,t)={\Psi }_0\sin \left(kx-\omega t)\right)}$

donde k es el número de onda, ω es la frecuencia angular, y v=ω/k es la velocidad de propagación

La ecuación de una onda, es la superposición

${\displaystyle \Psi (x,t)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}a(k)\exp \left(i(kx-\omega t)\right)}dk}$

En un medio dispersivo la frecuencia angular ω depende del número de onda k, las ondas de diferentes longitudes de onda λ=2π/k se propagan con distinta velocidad.

Al final de la página titulada Transformada de Fourier, hemos calculado la transformada de Fourier de la función.

${\displaystyle \begin{array}{l}\Psi (x\mathrm{,0})=\exp (i{k}_{0}x)·\exp \left(-\frac{{\left(x-x_0\right)}^2}{2{\sigma }_x^2}\right)\\ a(k)=A\exp \left(-ik{x}_0-\frac{{\left(k-k_0\right)}^2}{2{\sigma }_k^2}\right)\\ {\sigma }_x=\frac{1}{{\sigma }_k}\end{array}}$

Como hemos visto a(k) es una función que tiene un pico agudo centrado en k₀, por tanto, a(k) es distinto de cero en las proximidades de k₀ y es nula en el resto.

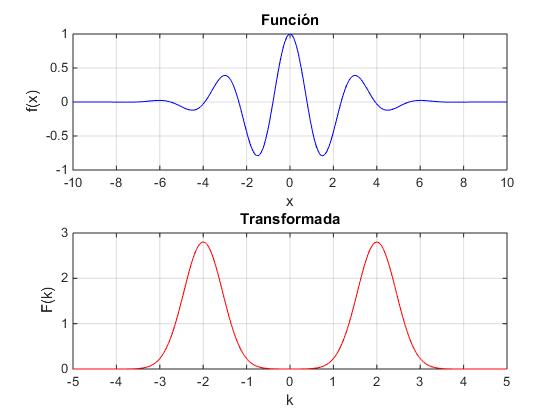
La fase φ(k)=kx-ωt es una función de k. Aproximamos φ(k) alrededor de k₀ (donde a(k) es distinto de cero) tomando los primeros términos del desarollo en serie de esta función.

${\displaystyle \phi (k)={\phi }_0+{\frac{d\phi }{dk}|}_0\left(k-k_0\right)+{\frac{1}{2}\frac{d^2\phi }{d{k}^2}|}_0{\left(k-k_0\right)}^2+\mathrm{...}}$

donde

${\displaystyle \begin{array}{l}{\phi }_0=k_{0}x-{\omega }_{0}t\\ {\frac{d\phi }{dk}|}_0=x-{\frac{d\omega }{dk}|}_{0}t=x-v_{g}t\\ {\frac{d^2\phi }{d{k}^2}|}_0=-{\frac{d^2\omega }{d{k}^2}|}_{0}t=-\alpha t\\ \phi (k)\approx k_{0}x-{\omega }_{0}t+(x-v_{g}t)\left(k-k_0\right)-\frac{1}{2}\alpha t{\left(k-k_0\right)}^2\end{array}}$

v_g de denomina velocidad de grupo de ondas, mientas que el cociente ω/k se denomina velocidad de fase.

Calculamos la ecuación de la onda en cualquier instante t

${\displaystyle \begin{array}{l}\Psi (x,t)=A{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-ik{x}_0-\frac{{\left(k-k_0\right)}^2}{2{\sigma }_k^2}+i\left(k_{0}x-{\omega }_{0}t+(x-v_{g}t)(k-k_0)-\frac{1}{2}\alpha t{\left(k-k_0\right)}^2\right)\right)}dk\\ \Psi (x,t)=A\exp \left(i(k_{0}x-{\omega }_{0}t-k_0{x}_0)\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-i(k-k_0)x_0-\frac{{\left(k-k_0\right)}^2}{2{\sigma }_k^2}+i\left((x-v_{g}t)(k-k_0)-\frac{1}{2}\alpha t{\left(k-k_0\right)}^2\right)\right)}dk\\ \Psi (x,t)=A\exp \left(i(k_{0}x-{\omega }_{0}t-k_0{x}_0)\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(i(x-x_0-v_{g}t)(k-k_0)-(i\alpha t{\sigma }_k^2+1)\frac{{\left(k-k_0\right)}^2}{2{\sigma }_k^2}\right)}dk\end{array}}$

Hacemos el cambio de variable y tenemos una integral del tipo descrito al final de la página titulada Transformada de Fourier o al principio del ejemplo 1 en esta página con

${\displaystyle \begin{array}{l}a=\frac{1}{\sqrt{2}\sigma },b=i\frac{y\sigma }{\sqrt{2}},c^2=\frac{{\sigma }^2{y}^2}{2}\\ \Psi (x,t)=A\exp \left(i(k_{0}x-{\omega }_{0}t-k_0{x}_0)\right)\sqrt{\pi }\frac{\exp \left(-c^2\right)}{a}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}u=k-k_0,du=dk\\ y=x-x_0-v_{g}t,\frac{1}{{\sigma }^2}=\frac{i\alpha t{\sigma }_k^2+1}{{\sigma }_k^2}=i\alpha t+\frac{1}{{\sigma }_k^2}\\ \Psi (x,t)=A\exp \left(i(k_{0}x-{\omega }_{0}t-k_0{x}_0)\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(iyu-\frac{u^2}{2{\sigma }^2}\right)}du\\ \Psi (x,t)=\sqrt{2\pi \frac{{\sigma }_k^2}{i\alpha t{\sigma }_k^2+1}}A\exp \left(i(k_{0}x-{\omega }_{0}t-k_0{x}_0)\right)\exp \left(-\frac{{\left(x-x_0-v_{g}t\right)}^2{\sigma }_k^2}{2(i\alpha t{\sigma }_k^2+1)}\right)\\ \Psi (x,t)=\sqrt{2\pi \frac{{\sigma }_k^2}{i\alpha t{\sigma }_k^2+1}}A\exp \left(i(k_{0}x-{\omega }_{0}t-k_0{x}_0)\right)\exp \left(-\frac{{\left(x-x_0-v_{g}t\right)}^2(1-i\alpha {\sigma }_k^{2}t)}{2\left({\alpha }^2{\sigma }_k^2{t}^2+\frac{1}{{\sigma }_k^2}\right)}\right)\end{array}}$

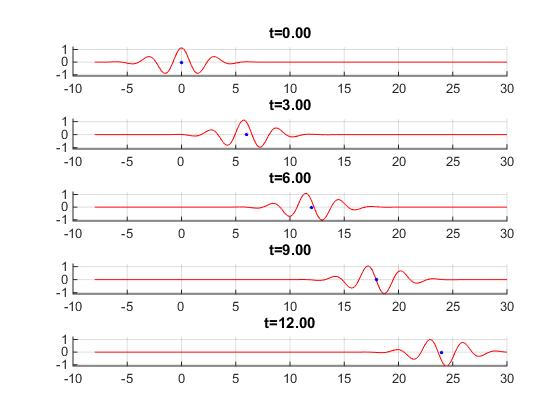
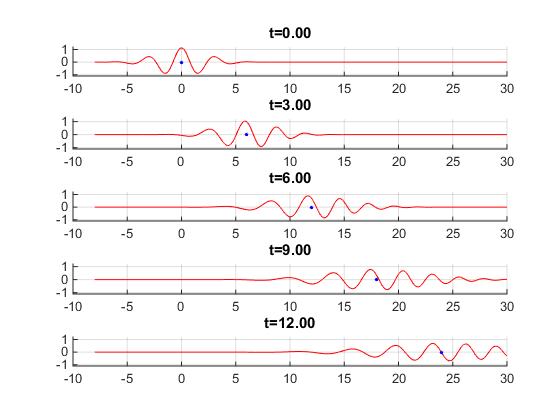
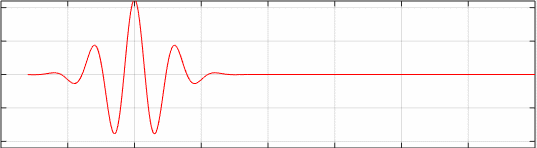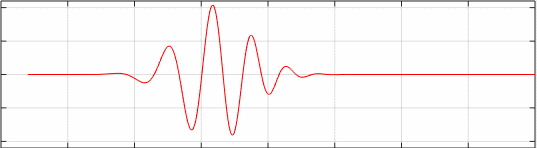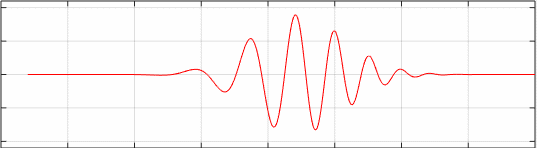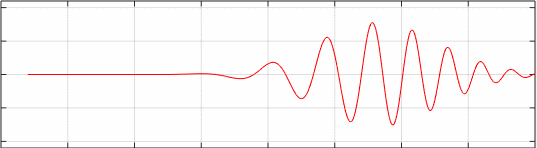
Propagación de un pulso sin distorsión, α=0, velocidad de grupo v_g=2. El punto de color azul marca el centro del grupo que se mueve con velocidad constante v_g.

x0=0; %posición inicial de la función de Gauss
k0=2; %número de onda
sx2=5; %extensión de la función de Gauss (cuadrado de sigma)
w0=4*k0; %velocidad de fase w0/k0
vg=2; %velocidad de grupo
alfa=0; %dispersión
sk2=1/sx2;
x=-8:0.02:30;

for i=1:5
    subplot(5,1,i)
    t=(i-1)*3;
    y=sqrt(2*pi*sk2/(1i*alfa*t*sk2+1))*exp(1i*(k0*x-w0*t-k0*x0))...
.*exp(-(x-x0-vg*t).^2*(1-1i*alfa*sk2*t)/(2*(alfa^2*sk2*t^2+1/sk2)));
    hold on
    plot(x,real(y),'r'); %movimiento ondulatorio
    plot(vg*t,0,'bo','markersize',2,'markerfacecolor','b') %centro del grupo
    hold off
    grid on
    ylim([-1.1,1.1])
    str=sprintf('t=%1.2f',t);
    title(str)
end

Propagación del pulso con distorsión α=1, velocidad de grupo v_g=2. El punto de color azul marca el centro del grupo.

Animamos la segunda figura

fichero = 'onda_2.gif';
hg=figure;
%posición y tamaño de la ventana gráfica
set(hg,'Position',[0,200,690,180]) 

x0=0; %posición inicial de la función de Gauss
k0=2; %número de onda
sx2=5; %extensión de la función de Gauss (cuadrado de sigma)
w0=4*k0; %velocidad de fase w0/k0
vg=2; %velocidad de grupo
alfa=1; %dispersión
sk2=1/sx2;
x=-8:0.02:30;
for t=0:0.1:10;
    y=sqrt(2*pi*sk2/(1i*alfa*t*sk2+1))*exp(1i*(k0*x-w0*t-k0*x0))...
.*exp(-(x-x0-vg*t).^2*(1-1i*alfa*sk2*t)/(2*(alfa^2*sk2*t^2+1/sk2)));
    plot(x,real(y),'r')
    ylim([-1.1,1.1])
    grid on
    
    %GIF animado
    frame=getframe;
    im = frame2im(frame);
    [imind,cm] = rgb2ind(im,256);
    if t==0
        imwrite(imind,cm,fichero,'gif','DelayTime',0,'loopcount',inf);
    else
        imwrite(imind,cm,fichero,'gif','DelayTime',0,'writemode','append');
    end
end

Ejemplo 1

En primer lugar, obtenemos el resultado de la integral

${\displaystyle \begin{array}{l}I={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-{\left(ax-b\right)}^2-c^2\right)dx}=\exp \left(-c^2\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-{\left(ax-b\right)}^2\right)dx}\hfill \\ \begin{array}{l}u=ax-b,du=a·dx\\ I=\frac{\exp \left(-c^2\right)}{a}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-u^2\right)du}=\sqrt{\pi }\frac{\exp \left(-c^2\right)}{a}\end{array}\hfill \end{array}}$

El resultado de la última integral se justifica en la página titulada Integrales

Medio no dispersivo

En un medio no dispersivo, la relación entre la frecuencia angular ω y el número de onda k es$\omega =\left|k\right|v$

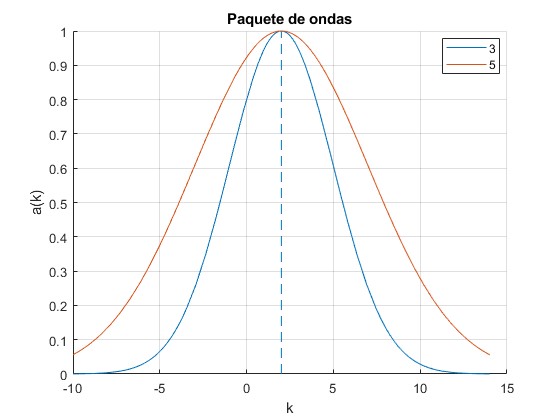
Sea a(k) una función de Gauss centrada en k₀. El parámetro Δk controla su anchura tal como se aprecia en la figura

${\displaystyle a(k)=\exp \left(-\frac{{\left(k-k_0\right)}^2}{2{\left(\Delta k\right)}^2}\right)}$

k0=2;
hold on
for Dk=[3,5]
    g=@(k) exp(-(k-k0).^2/(2*Dk^2));
    fplot(g,[-10,14])
end
line([k0,k0],[0,1],'lineStyle','--')
hold off
grid on
xlabel('k')
legend('3','5','location','best')
ylabel('a(k)')
title('Paquete de ondas')

Tenemos que calcular la integral

${\displaystyle \begin{array}{l}\Psi (x,t)=\frac{1}{\sqrt{2\pi }\Delta k}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}dk\exp \left(-\frac{{\left(k-k_0\right)}^2}{2{\left(\Delta k\right)}^2}\right)}\exp \left(i\left(kx-\omega t\right)\right)\\ \Psi (x,t)=\frac{1}{\sqrt{2\pi }\Delta k}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}dk\exp \left(-\frac{{\left(k-k_0\right)}^2}{2{\left(\Delta k\right)}^2}\right)}\exp \left(i\left(kx-v\left|k\right|t\right)\right)\end{array}}$

Esta integral es la suma de dos

${\displaystyle \Psi (x,t)=\frac{1}{\sqrt{2\pi }\Delta k}{\displaystyle \underset{-\infty }{\overset{0}{\int }}dk\exp \left(-\frac{{\left(k-k_0\right)}^2}{2{\left(\Delta k\right)}^2}\right)}\exp \left(i\left(kx+vkt\right)\right)+\frac{1}{\sqrt{\pi }\Delta k}{\displaystyle \underset{0}{\overset{\infty }{\int }}dk\exp \left(-\frac{{\left(k-k_0\right)}^2}{2{\left(\Delta k\right)}^2}\right)}\exp \left(i\left(kx-vkt\right)\right)}$

Resolvemos la primera integral

${\displaystyle \begin{array}{l}-\frac{{\left(k-k_0\right)}^2}{2{\left(\Delta k\right)}^2}+ik\left(x+vt\right)=-{\left(ak-b\right)}^2-c^2\\ -\frac{1}{2{\left(\Delta k\right)}^2}{k}^2+\left(\frac{k_0}{{\left(\Delta k\right)}^2}+i\left(x+vt\right)\right)k-\frac{k_0^2}{2{\left(\Delta k\right)}^2}=-a^2{k}^2+2abk-b^2-c^2,\\ \{\begin{array}{l}a=\frac{1}{\Delta k\sqrt{2}}\\ 2ab=\left(\frac{k_0}{{\left(\Delta k\right)}^2}+i\left(x+vt\right)\right),b=\frac{1}{\sqrt{2}}\left(\frac{k_0}{\Delta k}+i\left(x+vt\right)\Delta k\right)\\ -b^2-c^2=-\frac{k_0^2}{2{\left(\Delta k\right)}^2}\\ \frac{1}{2}{\left(\frac{k_0}{\Delta k}+i\left(x+vt\right)\Delta k\right)}^2+c^2=\frac{k_0^2}{2{\left(\Delta k\right)}^2}\\ c^2=\frac{1}{2}{\left(x+vt\right)}^2{\left(\Delta k\right)}^2-i{k}_0\left(x+vt\right)\end{array}\\ \frac{1}{\sqrt{2\pi }\Delta k}\Delta k\sqrt{2}\frac{\sqrt{\pi }}{2}\exp \left(-\frac{1}{2}{\left(x+vt\right)}^2{\left(\Delta k\right)}^2+i{k}_0\left(x+vt\right)\right)\end{array}}$

De modo análogo, se calcula la segunda integral. El resultado es

${\displaystyle \Psi (x,t)=\frac{1}{2}\exp \left(-\frac{1}{2}{\left(x+vt\right)}^2{\left(\Delta k\right)}^2\right)\exp \left(i{k}_0\left(x+vt\right)\right)+\frac{1}{2}\exp \left(-\frac{1}{2}{\left(x-vt\right)}^2{\left(\Delta k\right)}^2\right)\exp \left(i{k}_0\left(x-vt\right)\right)}$

Se ha tenido en cuenta el resultado

${\displaystyle {\displaystyle \underset{-\infty }{\overset{0}{\int }}\exp \left(-u^2\right)du=}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-u^2\right)du}=\frac{\sqrt{\pi }}{2}}$

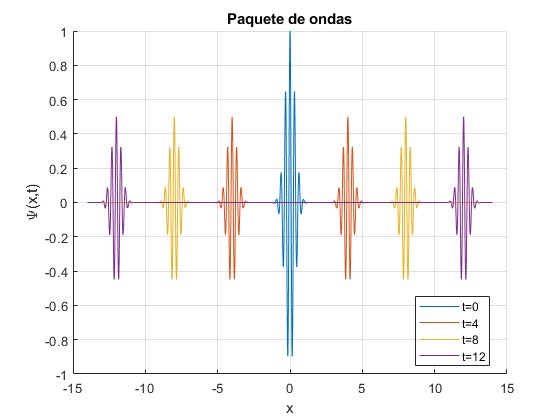
Ψ(x,t) representa una onda que se propaga sin distorsión a lo largo del eje X, hacia la derecha y hacia la izquierda, centradas en x=vt y x=-vt, modulada en amplitud

v=1; %velocidad de propagación
k0=20;
Dk=3;
hold on
f=@(x,t) (exp(-Dk^2*(x+v*t).^2/2).*exp(1i*k0*(x+v*t))+
exp(-Dk^2*(x-v*t).^2/2).*exp(1i*k0*(x-v*t)))/2;
for t=[0,4,8,12]
    g=@(x) real(f(x,t));
    fplot(g,[-14,14])
end
hold off
grid on
xlabel('x')
legend('t=0','t=4','t=8','t=12','location','best')
ylabel('\Psi(x,t)')
title('Paquete de ondas')

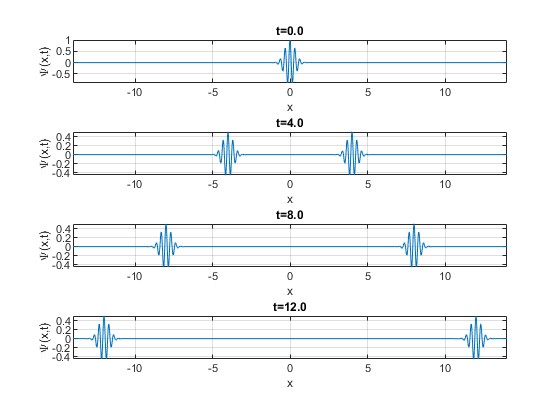
Otra forma de ver la figura anterior

v=1; %velocidad de propagación
k0=20;
Dk=3;
f=@(x,t) (exp(-Dk^2*(x+v*t).^2/2).*exp(1i*k0*(x+v*t))+
exp(-Dk^2*(x-v*t).^2/2).*exp(1i*k0*(x-v*t)))/2;
for i=0:3
    subplot(4,1,i+1)
    t=i*4;
    g=@(x) real(f(x,t));
    fplot(g,[-14,14])
    grid on
    xlabel('x')
    ylabel('\Psi(x,t)')
    str=sprintf('t=%1.1f',t);
    title(str)
end

Medio dispersivo

En este medio dispersivo, la relación entre la frecuencia angular ω y el número de onda k es no lineal, por ejemplo, $\omega =\gamma k^2$

Tenemos que calcular la integral

${\displaystyle \begin{array}{l}\Psi (x,t)=\frac{1}{\sqrt{2\pi }\Delta k}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}dk\exp \left(-\frac{{\left(k-k_0\right)}^2}{2{\left(\Delta k\right)}^2}\right)}\exp \left(i\left(kx-\omega t\right)\right)\\ \Psi (x,t)=\frac{1}{\sqrt{2\pi }\Delta k}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}dk\exp \left(-\frac{{\left(k-k_0\right)}^2}{2{\left(\Delta k\right)}^2}\right)}\exp \left(i\left(kx-\gamma k^{2}t\right)\right)\end{array}}$

Utilizando el resultado del ejemplo 1

${\displaystyle \begin{array}{l}-\frac{{\left(k-k_0\right)}^2}{2{\left(\Delta k\right)}^2}+i\left(kx-\gamma k^{2}t\right)=-{\left(ak-b\right)}^2-c^2\\ -\left(\frac{1}{2{\left(\Delta k\right)}^2}+i\gamma t\right)k^2+\left(\frac{k_0}{{\left(\Delta k\right)}^2}+ix\right)k-\frac{k_0^2}{2{\left(\Delta k\right)}^2}=-a^2{k}^2+2abk-b^2-c^2,\\ \{\begin{array}{l}{a}^2=\frac{1}{2{\left(\Delta k\right)}^2}+i\gamma t\\ 2ab=\frac{k_0}{{\left(\Delta k\right)}^2}+ix,b=\frac{1}{\sqrt{2}\Delta k}\frac{k_0+ix{\left(\Delta k\right)}^2}{\sqrt{1+2i\gamma {\left(\Delta k\right)}^{2}t}}\\ -b^2-c^2=-\frac{k_0^2}{2{\left(\Delta k\right)}^2}\\ \frac{1}{2{\left(\Delta k\right)}^2}\frac{{\left(k_0+ix{\left(\Delta k\right)}^2\right)}^2}{1+2i\gamma {\left(\Delta k\right)}^{2}t}+c^2=\frac{k_0^2}{2{\left(\Delta k\right)}^2}\\ c^2=\frac{k_0^2-\frac{{\left(k_0+ix{\left(\Delta k\right)}^2\right)}^2}{1+2i\gamma {\left(\Delta k\right)}^{2}t}}{2{\left(\Delta k\right)}^2}=\frac{2i\gamma k_0^2{\left(\Delta k\right)}^{2}t+x^2{\left(\Delta k\right)}^4-2i{k}_{0}x{\left(\Delta k\right)}^2}{2{\left(\Delta k\right)}^2\left(1+2i\gamma {\left(\Delta k\right)}^{2}t\right)}\end{array}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\Psi (x,t)=\frac{1}{\sqrt{2\pi }\Delta k}\frac{1}{\sqrt{\frac{1}{2{\left(\Delta k\right)}^2}+i\gamma t}}\sqrt{\pi }\exp \left(-\frac{2i\gamma k_0^{2}t+x^2{\left(\Delta k\right)}^2-2i{k}_{0}x}{2\left(1+2i\gamma {\left(\Delta k\right)}^{2}t\right)}\right)=\\ \frac{1}{\sqrt{1+2i\gamma {\left(\Delta k\right)}^{2}t}}\exp \left(-\frac{\frac{1}{2}{x}^2{\left(\Delta k\right)}^2-i{k}_0\left(x-\gamma k_{0}t\right)}{1+2i\gamma {\left(\Delta k\right)}^{2}t}\right)\\ \Psi (x,t)=\frac{1}{\sqrt{1+2i\gamma {\left(\Delta k\right)}^{2}t}}\exp \left(-\frac{\frac{1}{2}{\left(\Delta k\right)}^2{\left(x-2\gamma k_{0}t\right)}^2-i\left(k_0\left(x-\gamma k_{0}t\right)+x^2{\left(\Delta k\right)}^4\gamma t\right)}{1+4{\gamma }^2{\left(\Delta k\right)}^4{t}^2}\right)\end{array}}$

La amplitud es proporcional a

${\displaystyle \exp \left(-\frac{1}{2}{\left(\Delta k\right)}^2{\left(x-2\gamma k_{0}t\right)}^2\right)}$

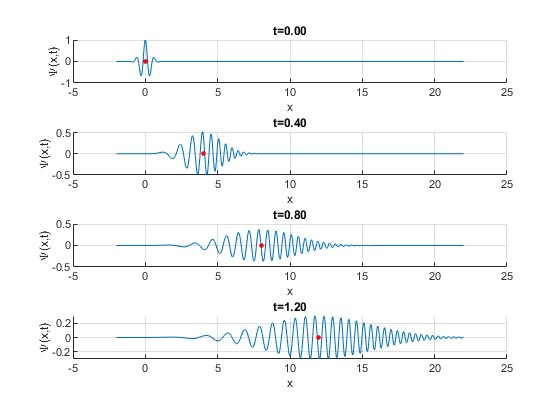
El valor máximo de la amplitud se obtiene para x=2γk₀t. Marcamos con un punto de color rojo en las figuras los centros x_p de los paquetes de ondas, que se mueven con la velocidad de grupo

${\displaystyle \begin{array}{l}{v}_g=\frac{d\omega }{dk}=2\gamma k\\ x_p=2\gamma k_{0}t\end{array}}$

k0=10;
Dk=3;
gamma=0.5;
f=@(x,t) exp(-(x.^2*Dk^2/2-1i*k0*(x-gamma*k0*t))/(1+2*1i*gamma*Dk^2*t))
/sqrt(1+2*1i*gamma*Dk^2*t);
for i=0:3
    subplot(4,1,i+1)
    t=i*0.4;
    g=@(x) real(f(x,t));
    hold on
    fplot(g,[-2,22])
     %centro del grupo
    plot(2*gamma*k0*t,0,'ro','markersize',3,'markerfacecolor','r')
    hold off
    grid on
    xlabel('x')
    ylabel('\Psi(x,t)')
    str=sprintf('t=%1.2f',t);
    title(str)
end

Ejemplo 2

La ecuación diferencial que describe la vibración de una barra elástica

${\displaystyle {\lambda }^2\frac{{\partial }^{4}y}{\partial x^4}+\frac{{\partial }^{2}y}{\partial t^2}=0}$

Buscamos una solución de la forma

${\displaystyle \begin{array}{l}y(x,t)=A\exp \left(i\left(kx-\omega t\right)\right)\\ \omega =\lambda k^2\end{array}}$

Obtenemos una relación entre la frecuencia angular ω y el número de onda k que no es lineal (como en un medio no dispersivo)

La solución de la ecuación diferencial es la superposición

${\displaystyle y(x,t)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}A(k)\exp \left(i\left(kx-\omega (k)t\right)\right)}}$

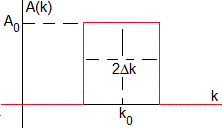
Consideremos el caso, en el que la amplitud A(k) es no nula en un pequeño intervalo

${\displaystyle A(k)=\{\begin{array}{l}{A}_0,k_0-\Delta k<k<k_0+\Delta k\\ \mathrm{0,}\text{el resto}\end{array}}$

El desplazamiento de los puntos de la barra es

${\displaystyle y(x,t)=A_0{\displaystyle \underset{k_0-\Delta k}{\overset{k_0+\Delta k}{\int }}\cos \left(kx-\lambda k^{2}t\right)dk}}$

Esta integral no es sencilla. El resultado que proporciona Math Symbolic de MATLAB es el siguiente. Se ha sustituido el parámetro λ por la variable a.

>> syms x k a t;
>> z=int(cos(k*x-a*k^2*t),k)
z =pi^(1/2)*cos(x^2/(4*a*t))*fresnelc((2^(1/2)*(x/2 - 
a*k*t)*(-1/(a*t))^(1/2))/pi^(1/2))*(-1/(2*a*t))^(1/2) - 
pi^(1/2)*sin(x^2/(4*a*t))*fresnels((2^(1/2)*(x/2 - a*k*t)*
(-1/(a*t))^(1/2))/pi^(1/2))*(-1/(2*a*t))^(1/2)

Mediante el comando

>> latex(z)

La respuesta ans se transforma en código Latex que copiamos y pegamos en el programa MathType, que a su vez, lo transforma en código MathML

${\displaystyle \sqrt{\pi }\cos \left(\frac{x^2}{4\lambda t}\right)\text{C}\left(\frac{\sqrt{2}\left(\frac{x}{2}-\lambda kt\right)\sqrt{-\frac{1}{\lambda t}}}{\sqrt{\pi }}\right)\sqrt{-\frac{1}{2\lambda t}}-\sqrt{\pi }\sin \left(\frac{x^2}{4\lambda t}\right)\text{S}\left(\frac{\sqrt{2}\left(\frac{x}{2}-\lambda kt\right)\sqrt{-\frac{1}{\lambda t}}}{\sqrt{\pi }}\right)\sqrt{-\frac{1}{2\lambda t}}}$

Teniendo en cuenta que

${\displaystyle \begin{array}{l}\sqrt{-z}=i\sqrt{z}\\ C(ix)=iC(x)\\ S(ix)=-iS(x)\end{array}}$

donde

${\displaystyle S(z)={\displaystyle \underset{0}{\overset{z}{\int }}\sin \left(\frac{\pi t^2}{2}\right)dt},C(z)={\displaystyle \underset{0}{\overset{z}{\int }}\cos \left(\frac{\pi t^2}{2}\right)dt}}$

son las integrales de Fresnel

El desplazamiento de los puntos de la barra elástica es

${\displaystyle \begin{array}{l}y(x,t)=-A_0\sqrt{\frac{\pi }{2\lambda t}}{\left\{\cos \left(\frac{x^2}{4\lambda t}\right)\text{C}\left(\frac{x-2\lambda kt}{\sqrt{2\pi \lambda t}}\right)+\sin \left(\frac{x^2}{4\lambda t}\right)\text{S}\left(\frac{x-2\lambda kt}{\sqrt{2\pi \lambda t}}\right)\right\}}_{k_0-\Delta k}^{k_0+\Delta k}=\\ -A_0\sqrt{\frac{\pi }{2\lambda t}}\left\{\cos \left(\frac{x^2}{4\lambda t}\right)\left\{\text{C}\left(\frac{x-2\lambda \left(k_0+\Delta k\right)t}{\sqrt{2\pi \lambda t}}\right)-\text{C}\left(\frac{x-2\lambda \left(k_0-\Delta k\right)t}{\sqrt{2\pi \lambda t}}\right)\right\}+\sin \left(\frac{x^2}{4\lambda t}\right)\left\{S\left(\frac{x-2\lambda \left(k_0+\Delta k\right)t}{\sqrt{2\pi \lambda t}}\right)-S\left(\frac{x-2\lambda \left(k_0-\Delta k\right)t}{\sqrt{2\pi \lambda t}}\right)\right\}\right\}\end{array}}$

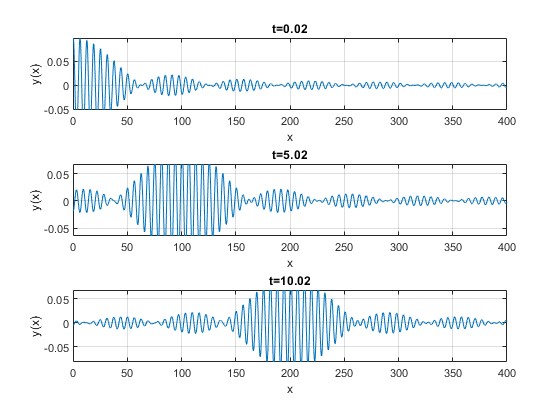
Representamos esta función en los instantes t=0.02, 5.02 y 10.02, para los valores de los parámetros

• k₀=1
• λ=10
• Δk=0.05

syms t x lambda k0 dk;
y=-sqrt(pi/(2*lambda*t))*(cos(x.^2/(4*lambda*t)).*
(fresnelc((x-2*lambda*t*(k0+dk))/sqrt(2*pi*lambda*t))-
fresnelc((x-2*lambda*t*(k0-dk))/sqrt(2*pi*lambda*t)))+
sin(x.^2/(4*lambda*t)).*(fresnels((x-2*lambda*t*(k0+dk))/
sqrt(2*pi*lambda*t))-fresnels((x-2*lambda*t*(k0-dk))/sqrt(2*pi*lambda*t))));

subplot(3,1,1)
y1=subs(y,{t,lambda,dk, k0},{0.02,10,0.05,1});
fplot(y1,[0,400])
grid on
xlabel('x')
ylabel('y(x)')
title('t=0.02')

subplot(3,1,2)
y1=subs(y,{t,lambda,dk, k0},{5.02,10,0.05,1});
fplot(y1,[0,400])
grid on
xlabel('x')
ylabel('y(x)')
title('t=5.02')

subplot(3,1,3)
y1=subs(y,{t,lambda,dk, k0},{10.02,10,0.05,1});
fplot(y1,[0,400])
grid on
xlabel('x')
ylabel('y(x)')
title('t=10.02')

Referencias

Masatsugu Suzuki. Lecture Notes of General Physics I and II Calculus Based. Topic 5. Waves and oscillations

David Romero-Abad, Roberto Suárez-Córdova. Energy transported by mechanical waves - two interesting examples: waves on a string and waves on a bar. No publicado