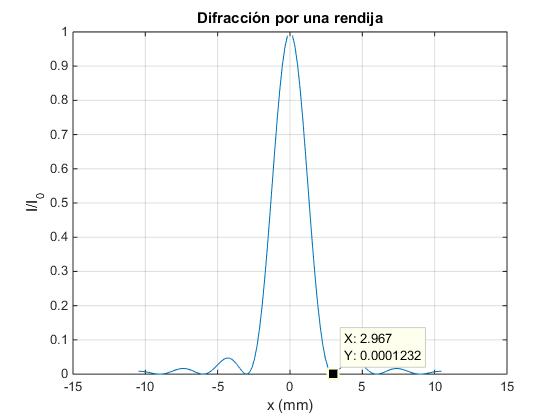
Difracción producida por una rendija
De acuerdo con el principio de Huygens, cuando la onda incide sobre una rendija todos los puntos de su plano se convierten en fuentes secundarias de ondas, emitiendo nuevas ondas, denominadas ondas difractadas, por lo que la explicación del fenómeno de la difracción no es cualitativamente distinto de la interferencia. Una vez que hemos estudiado la interferencia de un número limitado de fuentes, la difracción se explica a partir de la interferencia de un número infinito de fuentes.
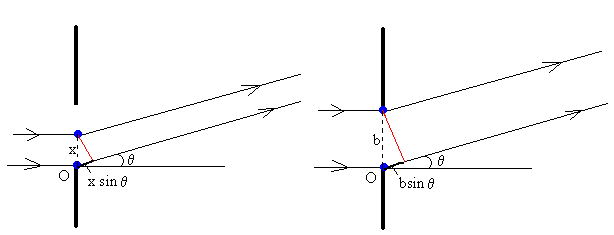
Sea b la anchura de la rendija, y consideremos que las infinitas fuentes secundarias de ondas están distribuidas a lo largo de la rendija.
- La diferencia de caminos entre la fuente que pasa por el origen y la que pasa por el punto x es, x·sinθ .
- La diferencia de caminos entre la fuente situada en el origen y la situada en el otro extremo de la rendija será b·sinθ .
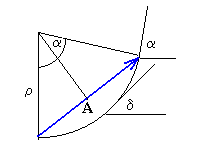
El estado del punto P es la superposición de infinitos M.A.S. La suma de los infinitos vectores de amplitud infinitesimal produce un arco de circunferencia, cuya cuerda es la resultante A.
El ángulo δ que forma el vector situado en x con la horizontal vale kx·sinθ .
El ángulo α que forma el vector situado en x=b con la horizontal vale, kb·sinθ =2πb·sinθ /λ . Este ángulo es el mismo que el que subtiende el arco de la circunferencia de radio ρ.
Calculamos la longitud de la cuerda, es decir, la resultante.
Eliminando el radio ρ, queda
y como las intensidades son proporcionales a los cuadrados de las amplitudes
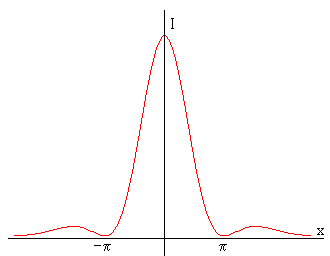
El máximo de la difracción se produce cuando el argumento del seno es cero, ya que
Para que dicho argumento sea cero, el ángulo θ debe ser cero. Tenemos un máximo de intensidad en el origen, en la dirección perpendicular al plano de la rendija.
Mínimos de intensidad
Los mínimos de intensidad se producen cuando el argumento del seno es un múltiplo entero de π, es decir, cuando
o bien, cuando b·sinθ =nλ (n=1, 2, 3...)
Esta es la fórmula que describe el fenómeno de la difracción Fraunhofer producido por una rendija estrecha.
Máximos secundarios
Los máximos y mínimos se calculan derivando la fórmula de la intensidad respecto de x=πb·sinθ /λ
-
Cuando sinx/x =0 tenemos un mínimo de intensidad, pues I=0
-
Cuando xcosx-sinx=0 o bien, cuando x=tanx tenemos un máximo de intensidad
Por ejemplo cuando x=0, pero también para otros valores de x que son las raíces de la ecuación trascendente x=tanx. Estas raíces se pueden calcular numéricamente o gráficamente.
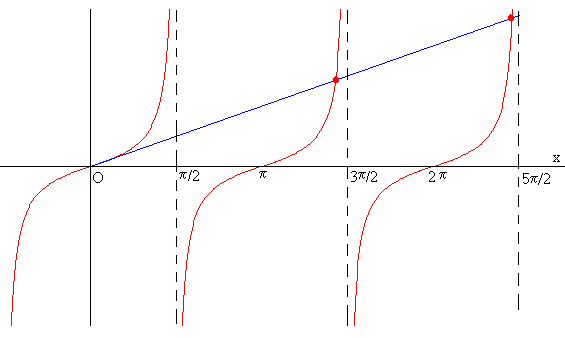
Como observamos en la gráfica los máximos secundarios ocurren aproximadamente para xn≈(2n+1)π/2 donde n=±1, ±2, ±3…
Teniendo en cuenta que sin(xn)=1. La intensidad debida a la difracción en la dirección correspondiente a los máximos secundarios es aproximadamente igual a
que como vemos decrece rápidamente a medida que se incrementa n.
Para calcular las posiciones de los máximos secundarios, representamos la función y=xcosx-sinx y calculamos sus intersecciones con el eje X en el intervalo especificado
x=linspace(0,7*pi/2,100);
y=x.*cos(x)-sin(x);
plot(x,y)
xlabel('x')
ylabel('y')
title('Difracción por una rendija')
grid on
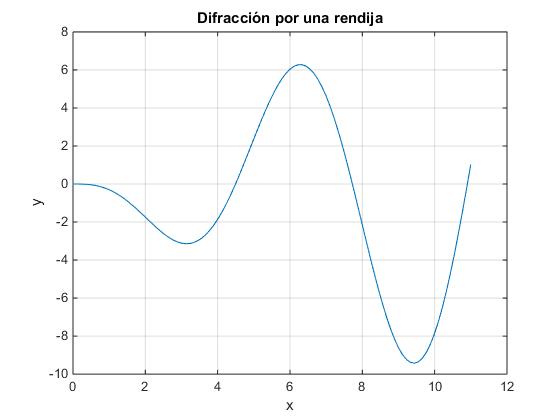
>> f=@(x) x.*cos(x)-sin(x); >> x=linspace(0.1,7*pi/2,50); >> raices(f,x) ans = 4.4934 7.7253 10.9041
La primera raíz es próxima a 3π/2=4.7124, la segunda, es próxima 5π/2=7.8540 y la tercera es próxima a 7π/2=10.9956.
Actividades
Se introduce
- La anchura de la rendija b, en el control titulado Anchura rendija.
- La longitud de onda λ en el control titulado longitud onda.
- el número de fuentes secundarias, en el control titulado nº de fuentes de ondas, que situamos en la rendija. Cuanto mayor sea el número de fuentes secundarias mejor se reproduce la difracción producida por la rendija, mayor es también el tiempo que emplea el ordenador en mostrar los resultados.
Se pulsa el botón titulado Nuevo
Se muestra las ondas planas incidentes sobre una rejilla y las ondas difractadas como si fuese una fotografía tomada de una cubeta de ondas.
A continuación, se muestra la intensidad en la posición x=200, codificada en escala de grises. La máxima intensidad en color blanco, la intensidad cero en color negro. Finalmente, la representación gráfica de la intensidad en dicha posición, en el borde derecho de la "cubeta de ondas"
Ejemplo:
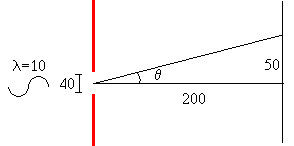
Se introduce
- Longitud de onda, λ=10
- Anchura de la rendija, b=40
- Se seleccionan 20 fuentes secundarias
Se observa el primer mínimo de difracción en la posición y=50. Primero, calculamos el ángulo tanθ=50/200, y luego, comprobamos que b·sinθ≈λ
Se ha de tener en cuenta que en la difracción Fraunhofer, el observador se encuentra a una distancia grande en comparación con la anchura de la rendija y esta condición no se cumple en esta simulación. Su objetivo no es el cálculo de los mínimos de difracción sino la de mostrar que la difracción no es un fenómeno cualitativamente distinto de la interferencia.
Difracción del espectro de la luz visible
La luz visible es una región del espectro electromagnético comprendida entre 780 a 390 nm. Las diferentes sensaciones que la luz produce en el ojo, se denominan colores, dependen de la frecuencia (o de la longitud de onda electromagnética) y corresponden a los siguientes intervalos para una persona promedio:
| Región | Frecuencia (1012 Hz) | Longitud de onda en 10-9 m |
|---|---|---|
| Rojo | 384-482 | 780-622 |
| Naranja | 482-503 | 622-597 |
| Amarillo | 503-520 | 597-577 |
| Verde | 520-610 | 577-492 |
| Azul | 610-659 | 492-455 |
| Violeta | 659-769 | 455-390 |
Fuente: Hetch-Zajac. Optica. Addison-Wesley Iberoamericana (1986), pág 60
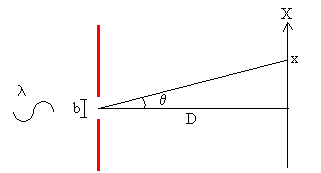
Iluminamos una rendija de anchura b, con luz del espectro visible, observamos la difracción (intensidad) en una pantalla situada a D de distancia de la rendija.
Determinar los primeros mínimos de la intensidad de difracción.
b·sinθ=nλ
Posición de los mínimos de difracción en la pantalla
x=D·tanθ
Ejemplo:
- Longitud de onda, λ=600 nm=600·10-9 m
- Anchura de la rendija, b=0.2 mm=0.2·10-3 m
- Distancia de la rendija a la pantalla, D=1 m
| Mínimo, n | Posición, x (mm) |
|---|---|
| 1 | 3.0 |
| 2 | 6.0 |
| 3 | 9.0 |
Si el ángulo θ es pequeño, tanθ≈sinθ
Creamos un programa en MATLAB para representar la intensidad en función de x cuando le proporcionamos los datos de la longitud de onda λ, la anchura de la rendija b y la distancia D a la pantalla
lonOnda=600e-9; %en m
a=0.2e-3; %en m
D=1; % distancia a la pantalla en m
angulo=(-0.6:0.01:0.6)*pi/180;
x=pi*a*sin(angulo)/lonOnda;
y=((sin(x).^2)./x.^2).*(abs(x)>eps)+(abs(x)<eps);
plot(D*tan(angulo)*1000,y)
xlabel('x (mm)')
ylabel('I/I_0')
title('Difracción por una rendija')
grid on