El principio de Fermat

Ley de la reflexión

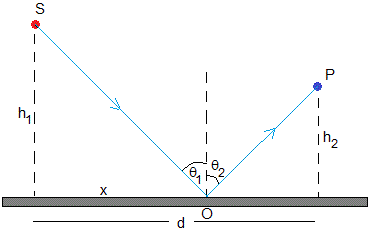
Sea una fuente S que emite un rayo que se reflejan en una superficie horizontal reflectante, en O y llega al observador situado en el punto P. La luz se propaga en el mismo medio homogéneo, con velocidad c

La longitud del camino seguido por este rayo es SOP y el tiempo que emplea es la suma del tiempo que tarda en recorrer los caminos SO y OP

x es la distancia de S a O, d-x es la distancia de P a O. h₁ es la distancia de S al espejo y h₂ es la distancia de P al espejo

$t = \frac{\sqrt{h_{1}^{2} + x^{2}}}{c} + \frac{\sqrt{h_{2}^{2} + {(d - x)}^{2}}}{c}$

Derivamos el tiempo t respecto de x e igualamos a cero

$\begin{array}{l} \frac{d t}{d x} = \frac{x}{c \sqrt{h_{1}^{2} + x^{2}}} - \frac{d - x}{c \sqrt{h_{2}^{2} + {(d - x)}^{2}}} = 0 \\ \frac{\sin θ_{1}}{c} = \frac{\sin θ_{2}}{c} \\ θ_{1} = θ_{2} \end{array}$

Como vemos en la figura, θ₁ es el ángulo que hace el rayo incidente con la normal al espejo y θ₂ es el ángulo que hace el rayo reflejado

Ley de la refracción

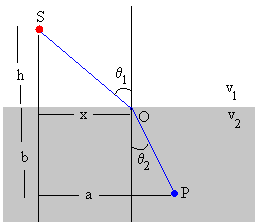
Calculamos el tiempo que tarda un rayo de luz en ir de la fuente S hasta llegar al observador P. El primer tramo SO lo recorre en el primer medio con velocidad v₁ y el segundo tramo OP lo recorre en el segundo medio con una velocidad v₂.

$t = \frac{S O}{v_{1}} + \frac{O P}{v_{2}} = \frac{\sqrt{h^{2} + x^{2}}}{v_{1}} + \frac{\sqrt{b^{2} + {(a - x)}^{2}}}{v_{2}}$

El tiempo t es una función de la posición x de O. La función t(x) tendrá un mínimo en la posición x en la que se cumple que la derivada primera de t respecto de x a cero

$\frac{d t}{d x} = \frac{x}{v_{1} \sqrt{h^{2} + x^{2}}} + \frac{- (a - x)}{v_{2} \sqrt{b^{2} + {(a - x)}^{2}}} = 0$

Esto es equivalente a escribir

$\frac{sin θ_{1}}{v_{1}} = \frac{sin θ_{2}}{v_{2}}$

Se define el índice de refracción n de un medio como el cociente de la velocidad de la luz en el vacío c entre la velocidad v de propagación de la luz en dicho medio, n=c/v.

La ley de Snell de la refracción se escribe: n₁·sinθ₁=n₂·sinθ₂

Actividades

Se introduce

La velocidad de la luz en el primer medio v₁, en el control titulado Velocidad A
La velocidad de la luz en el segundo medio v₂, en el control titulado Velocidad B

Se representa la fuente S en la parte superior y el observador P en la parte inferior. Sus posiciones se asignan aleatoriamente dentro de ciertos límites.

La posición x del punto O, en la superficie de separación entre los dos medios, se puede modificar en el control titulado Posición

Se pulsa el botón titulado Nuevo.

Se traza el camino SOP y se calcula el tiempo que tarda la luz en recorrerlo. Se mueve el punto O hacia la izquierda o hacia la derecha hasta encontrar la trayectoria real SOP seguida por el rayo de luz. Para ayudarnos en esta tarea, se proporciona en la parte superior izquierda, el tiempo empleado por el rayo de luz en recorrer la trayectoria actual y el tiempo empleado por el rayo de luz en recorrer la trayectoria anterior. Para encontrar la trayectoria seguida por el rayo de luz el tiempo actual tiene que ser siempre inferior al tiempo anterior

Cuando se encuentra la trayectoria SOP real que sigue el rayo de luz, se representa el rayo incidente, el refractado y se proporcionan los datos del ángulo de incidencia y de refracción. Con estos datos comprobamos la ley de la refeacción

Ejemplo:

Introducimos los valores de las velocidades

en el primer medio (amarillo) v₁=1.0;
en el segundo medio (azul claro) v₂=4.0

Medimos en las escalas graduadas las posiciones de S, (punto de color azul en la parte superior) y P (punto de color azul en la parte inferior), generadas de forma aleatoria por el programa

Posición del emisor S (2.4, 3.3)
Posición del observador P (-3.1, -2.0)

Con el control denominado Posición movemos la cruz de color roja hasta la posición x=-1.8

Se pulsa el botón titulado Nuevo

El tiempo que emplea la luz en recorrer el camino SOP es

$t = \frac{\sqrt{{(2.4 - (- 1.8))}^{2} + {3.3}^{2}}}{1.0} + \frac{\sqrt{{(- 3.1 - (- 1.8))}^{2} + {(- 2.0)}^{2}}}{4.0} = 5.92$

Se mueve la cruz de color roja a otra posición y se vuelve a pulsar el botón titulado Nuevo. Así, hasta encontrar la trayectoria real seguida por un rayo de luz entre la posición S y la P.

Para la posición x=1.6 encontramos la trayectoria real SOP que sigue el rayo de luz.

El ángulo θ₁ que forma el rayo incidente con la normal a la superficie de separación es

$\begin{array}{l} \tan θ_{1} = \frac{x_{S} - x_{O}}{y_{S}} = \frac{2.4 - 1.6}{3.3} θ_{1} = 13.6 º \\ \tan θ_{2} = \frac{x_{P} - x_{O}}{y_{P}} = \frac{- 3.1 - 1.6}{- 2.0} θ_{2} = 67.0 º \end{array}$

Comprobamos la ley de Snell de la refracción

$\frac{sin θ_{1}}{v_{1}} = \frac{sin θ_{2}}{v_{2}} \frac{sin13 .6}{1.0} \approx \frac{sin67 .0}{4.0}$

Velocidad A: Velocidad B:
Posición:

Cálculo de la posición x

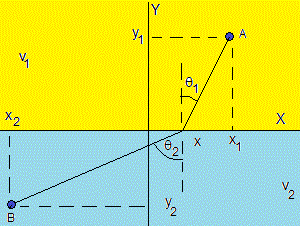
Consideremos el siguiente problema. Un bañista está en peligro de ahogarse en un río en la posición B (x₂,y₂), el socorrista está en tierra en la posición A (x₁,y₁). La velocidad de desplazamiento del socorrista en tierra es v₁ y en el agua es v₂. ¿Qué camino debería seguir el socorrista para llegar a B en el tiempo más corto posible?

Llamemos k=v₁/v₂. La ley de la refracción se escribe

$\begin{array}{l} \sin θ_{1} = \frac{v_{1}}{v_{2}} \sin θ_{2} \\ \frac{x_{1} - x}{\sqrt{y_{1}^{2} + {(x_{1} - x)}^{2}}} = k \frac{(x - x_{2})}{\sqrt{y_{2}^{2} + {(x - x_{2})}^{2}}} \end{array}$

Elevando al cuadrado, obtenemos la ecuación

${(x_{1} - x)}^{2} (y_{2}^{2} + {(x - x_{2})}^{2}) - k^{2} (y_{1}^{2} + {(x_{1} - x)}^{2}) {(x - x_{2})}^{2} = 0$

Utilizamos MATLAB para obtener las raíces de la ecuación en a₄x⁴+a₃x³+a₂x²+a₁x+a₀=0

>> syms k x x1 x2 y1 y2;
>> z=(x1-x)^2*(y2^2+(x-x2)^2)-k^2*(y1^2+(x1-x)^2)*(x-x2)^2;
>> collect(z)
ans =(1 - k^2)*x^4 + (2*k^2*x1 - 2*x2 - 2*x1 + 2*k^2*x2)*x^3 +
 (4*x1*x2 - k^2*(x1^2 + y1^2) - k^2*x2^2 + x1^2 + x2^2 + y2^2 - 
4*k^2*x1*x2)*x^2 + (2*k^2*x1*x2^2 - 2*x1*(x2^2 + y2^2) 
- 2*x1^2*x2 + 2*k^2*x2*(x1^2 + y1^2))*x + x1^2*(x2^2 + y2^2) -
 k^2*x2^2*(x1^2 + y1^2)

Probamos con los siguientes valores: k=v₁/v₂=1/4, x₁=1.6, y₁=4, x₂=-1.1, y₂=-2.4

>>  z1=subs(z,{k,x1,y1,x2,y2},{1/4,1.6,4,-1.1,-2.4});
>> collect(z1)
ans =(15*x^4)/16 - (15*x^3)/16 + (2711*x^2)/1600 - (9491*x)/500 + 41099/2500
>> solve(z1)
ans =
                                         2.4465320619722248043283614253126
                                        0.94309804430104907919242963600088
 - 2.4844300896274989917057297598565*i - 1.1948150531366369417603955306568
   2.4844300896274989917057297598565*i - 1.1948150531366369417603955306568

De las cuatro raíces, dos son complejas, y de las dos reales, solamente es válida la segunda, ya que la solución x deberá estar en el intervalo (x₁,x₂)

Ley de la reflexión para un espejo en movimiento

En este apartado deducimos la ley de la reflexión de un fotón de luz a partir del principio de Fermat y la constancia de la velocidad c de la luz.

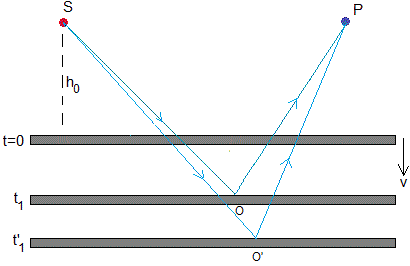
Consideremos un espejo en movimiento con velocidad v. Supongamos que la fuente S y el detector P se encuentran a la misma distancia del espejo h₀ en el instante t=0, en el que la fuente S emite un fotón. En la figura, se muestra dos posibles trayectorias del fotón desde la fuente S al espejo en movimiento y desde el espejo al detector P. El principio de Fermat, nos dice que el fotón seguirá aquella trayectoria en la cual emplee un tiempo mínimo en recorrerla

Consideraremos una posible trayectoria. En el instante t=0, la fuente S emite un fotón, el espejo se encuentra a una distancia h₀ de S. Se refleja en el espejo, en O, en el instante t₁. El espejo se encuentra a una distancia h₀+vt₁ de S y el fotón ha recorrido el camino SO en el mismo tiempo a una velocidad c. Sea x la distancia de O a S.

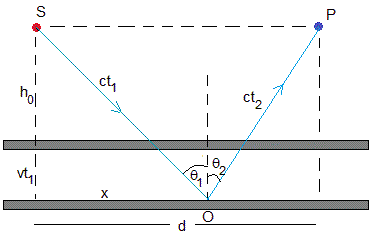
El tiempo t₁ vale

${(c t_{1})}^{2} = x^{2} + {(h_{0} + v t_{1})}^{2}$

El fotón se refleja en O y llega al detector P recorriendo el camino OP con la misma velocidad c, empleando un tiempo t₂

${(c t_{2})}^{2} = {(d - x)}^{2} + {(h_{0} + v t_{1})}^{2}$

El fotón tarda un tiempo t=t₁+t₂ en recorrer el camino SOP a la velocidad constante c, la posición x de O será tal que el fotón emplee un tiempo mínimo t en recorrerlo.

$t = t_{1} + t_{2} = \frac{1}{c} \sqrt{x^{2} + {(h_{0} + v t_{1})}^{2}} + \frac{1}{c} \sqrt{{(d - x)}^{2} + {(h_{0} + v t_{1})}^{2}}$

Derivamos el tiempo total t con respecto a x e igualamos a cero, teniendo en cuanta que t₁ es a su vez, una función de x.

$\begin{array}{l} \frac{d t}{d x} = \frac{v}{c} \frac{h_{0} + v t_{1}}{\sqrt{x^{2} + {(h_{0} + v t_{1})}^{2}}} \frac{d t_{1}}{d x} + \frac{1}{c} \frac{x}{\sqrt{x^{2} + {(h_{0} + v t_{1})}^{2}}} + \\ \frac{v}{c} \frac{h_{0} + v t_{1}}{\sqrt{{(d - x)}^{2} + {(h_{0} + v t_{1})}^{2}}} \frac{d t_{1}}{d x} - \frac{1}{c} \frac{d - x}{\sqrt{{(d - x)}^{2} + {(h_{0} + v t_{1})}^{2}}} = 0 \end{array}$

En términos de los ángulos θ₂ y θ₁, de los dos triángulos rectángulos, se expresa

$v \cos θ_{1} \frac{d t_{1}}{d x} + \sin θ_{1} + v \cos θ_{2} \frac{d t_{1}}{d x} - \sin θ_{2} = 0$

Calculamos la derivada dt₁/dx y la insertamos en esta ecuación

$\begin{array}{l} {(c t_{1})}^{2} = x^{2} + {(h_{0} + v t_{1})}^{2} \\ 2 c^{2} t_{1} \frac{d t_{1}}{d x} = 2 x + 2 v (h_{0} + v t_{1}) \frac{d t_{1}}{d x} \\ \frac{d t_{1}}{d x} = \frac{x}{c^{2} t_{1} - v (h_{0} + v t_{1})} = \frac{\frac{x}{c t_{1}}}{c (1 - \frac{v}{c} \frac{h_{0} + v t_{1}}{c t_{1}})} = \frac{\sin θ_{1}}{c (1 - \frac{v}{c} \cos θ_{1})} \end{array}$

Finalmente, la ecuación queda

$\sin θ_{1} - \sin θ_{2} + \frac{v}{c} \sin (θ_{1} + θ_{2}) = 0$

A primera vista parece que se trata de una ecuación transcendente, pero es posible despejar cosθ₂ en términos de θ₁

$(1 - \frac{v}{c} \cos θ_{1}) \sin θ_{2} = (1 + \frac{v}{c} \cos θ_{2}) \sin θ_{1}$

Elevamos al cuadrado para sustituir sin²θ₂=1-cos²θ₂, obteniendo una ecuación de segundo grado en cosθ₂

$\begin{array}{l} {(1 - \frac{v}{c} \cos θ_{1})}^{2} (1 - \cos^{2} θ_{2}) = {(1 + \frac{v}{c} \cos θ_{2})}^{2} (1 - \cos^{2} θ_{1}) \\ (1 + \frac{v^{2}}{c^{2}} - 2 \frac{v}{c} \cos θ_{1}) \cos^{2} θ_{2} + (2 \frac{v}{c} (1 - \cos^{2} θ_{1})) \cos θ_{2} + 2 \frac{v}{c} \cos θ_{1} - (1 + \frac{v^{2}}{c^{2}}) \cos^{2} θ_{1} = 0 \\ \cos θ_{2} = \frac{- \frac{v}{c} (1 - \cos^{2} θ_{1}) \pm \sqrt{\frac{v^{2}}{c^{2}} {(1 - \cos^{2} θ_{1})}^{2} - (1 + \frac{v^{2}}{c^{2}} - 2 \frac{v}{c} \cos θ_{1}) (2 \frac{v}{c} - (1 + \frac{v^{2}}{c^{2}}) \cos θ_{1}) \cos θ_{1}}}{(1 + \frac{v^{2}}{c^{2}} - 2 \frac{v}{c} \cos θ_{1})} \end{array}$

Utilizamos Math Symbolic de MATLAB para simplificar y factorizar el discriminante. Llamamos k a v/c y x a cosθ₁

>> syms k x;
>> y=k^2*(1-x^2)^2-(1+k^2-2*k*x)*(2*k*x-(1+k^2)*x^2);
>> factor(y)
 ans =[ k - x, k - x, k*x - 1, k*x - 1]

Las dos raíces de la ecuación de segundo grado son

$\begin{array}{l} \cos θ_{2} = \frac{- \frac{v}{c} (1 - \cos^{2} θ_{1}) \pm (\frac{v}{c} - \cos θ_{1}) (\frac{v}{c} \cos θ_{1} - 1)}{(1 + \frac{v^{2}}{c^{2}} - 2 \frac{v}{c} \cos θ_{1})} \\ {(\cos θ_{2})}_{1} = \frac{- 2 \frac{v}{c} + (1 + \frac{v^{2}}{c^{2}}) \cos θ_{1}}{(1 + \frac{v^{2}}{c^{2}} - 2 \frac{v}{c} \cos θ_{1})} \\ {(\cos θ_{2})}_{2} = \frac{2 \frac{v}{c} \cos^{2} θ_{1} - (1 + \frac{v^{2}}{c^{2}}) \cos θ_{1}}{(1 + \frac{v^{2}}{c^{2}} - 2 \frac{v}{c} \cos θ_{1})} \end{array}$

De las dos soluciones solamente una es correcta, probamos cuando el espejo está inmóvil v=0, el ángulo de incidencia tiene que ser igual al de reflexión, θ₁=θ₂

La primera solución, cosθ₂=cosθ₁
La segunda solución, cosθ₂=-cosθ₁ que no es correcta

La relación entre el ángulo de incidencia θ₁ y de reflexión θ₂, es

$\cos θ_{2} = \frac{(1 + \frac{v^{2}}{c^{2}}) \cos θ_{1} - 2 \frac{v}{c}}{(1 + \frac{v^{2}}{c^{2}} - 2 \frac{v}{c} \cos θ_{1})}$

En primer lugar, el fotón no se refleja en el espejo, si la componente vertical de su velocidad, c·cosθ₁ es menor que la velocidad v del espejo, c·cosθ₁<v. El ángulo máximo es cosθ_1m=v/c para v/c>0

Representamos el ángulo de reflexión θ₂ en función del ángulo de incidencia θ₁, para varios valores del cociente v/c positivos (cuando el espejo se aleja de las fuente) y negativos (cuando se acerca). Cuando v=0, (espejo inmóvil), el ángulo de incidencia y el de reflexión son iguales, θ₂=θ₁, la representación es una línea recta de pendiente la unidad

hold on
for k=-0.8:0.2:0.8 %cociente v/c
    f=@(x) acos(((1+k^2)*cos(x)-2*k)./(1+k^2-2*k*cos(x)));
    if k>0
        fplot(f,[0,acos(k)], 'displayName',num2str(k))
    else
        fplot(f,[0,pi/2], 'displayName',num2str(k))
    end
end
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','15','30','45','60','75','90'})
set(gca,'YTick',0:pi/6:pi)
set(gca,'YTickLabel',{'0','30','60','90','120','150','180'})
xlabel('\theta_1')
ylabel('\theta_2')
legend('-DynamicLegend','location','northwest')
title('Espejo móvil')

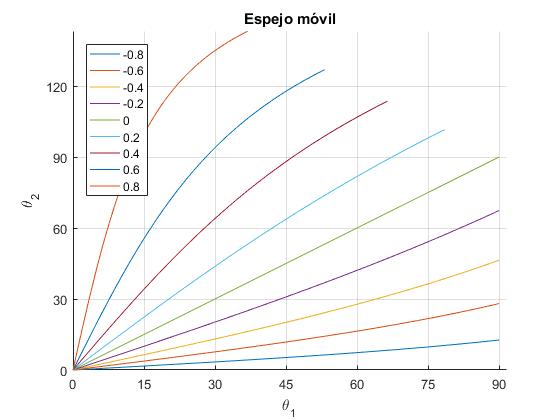
Cuando la velocidad del espejo v/c>0, hay un intervalo de valores para los que el ángulo θ₂>90°. El fotón reflejado se mueve en la misma dirección que el espejo. Calculamos el ángulo θ₁ crítico para el cual θ₂=90°

$\cos θ_{1 c} = 2 \frac{\frac{v}{c}}{1 + \frac{v^{2}}{c^{2}}}$

Por ejemplo, para v/c=0.2, θ_1c=67.4° y θ_1m=78.5°, tal como vemos en la gráfica de color azul claro, marcada con la etiqueta 0.2

Referencias

Aleksandar Gjurchinovski. Einstein's mirror and Fermat's principle of least time. Am. J. Phys. 72 (10) October 2004, pp. 1325-1327

Aleksandar Gjurchinovski. Reflection of light from a uniformly moving mirror. Am. J. Phys. 72 (10) October 2004, pp. 1316-1324

Aleksandar Gjurchinovski, Aleksandar Skeparovski. Einstein's mirror. The Physics Teacher, Vol. 46, October 2008, pp. 416-418