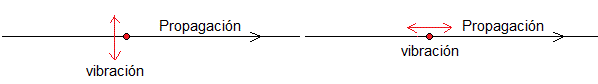
En un movimiento ondulatorio transversal, las direcciones de propagación y vibración de las partículas del medio son perpendiculares.

En un movimiento ondulatorio longitudinal, la propagación y la vibración de las partículas del tienen la misma dirección.

Ondas transversales en una cuerda

Consideremos una cuerda cuya tensión es T. En el equilibrio, la cuerda está en línea recta. Vamos a ver lo que ocurre cuando se desplaza un elemento de longitud dx, situado en la posición x de la cuerda, una cantidad Ψ respecto de la posición de equilibrio.

Dibujamos las fuerzas que actúan sobre el elemento diferencial y calculamos la aceleración del mismo, aplicando la segunda ley de Newton.

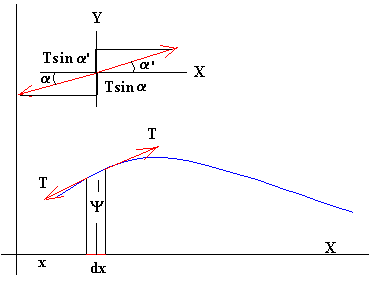
• La fuerza que ejerce la parte izquierda de la cuerda sobre el extremo izquierdo del elemento, es igual a la tensión T, la dirección es tangente a la cuerda en dicho punto, formando un ángulo α con la horizontal.
   
• La fuerza que ejerce la parte derecha de la cuerda sobre el extremo derecho del elemento, es igual a la tensión T, la dirección es tangente a la cuerda en dicho punto, formando un ángulo α’ con la horizontal.

Como el elemento se desplaza en la dirección vertical, hallamos las componentes de las dos fuerzas en esta dirección y la resultante.

T(sinα’-sinα )

Si la curvatura de la cuerda no es muy grande, los ángulos α’ y α son pequeños y sus senos se pueden reemplazar por tangentes.

${\displaystyle T(\tan \alpha \text{'}-\tan \alpha )=Td(\tan \alpha )=T\frac{\partial }{\partial x}(\tan \alpha )dx=T\frac{{\partial }^2\Psi }{\partial x^2}dx}$

La segunda ley de Newton nos dice que la fuerza sobre el elemento es igual al producto de su masa por la aceleración (derivada segunda del desplazamiento).

La masa del elemento es igual al producto de la densidad lineal μ (masa por unidad de longitud), por la longitud dx del elemento.

${\displaystyle (\mu dx)\frac{{\partial }^2\Psi }{\partial t^2}=T\frac{{\partial }^2\Psi }{\partial x^2}dx}$

Simplificando el término dx llegamos a la ecuación diferencial del Movimiento Ondulatorio,  a partir de la cual, obtenemos la fórmula de la velocidad de propagación de las ondas transversales en la cuerda.

${\displaystyle v=\sqrt{\frac{T}{\mu }}}$

• T es la tensión de la cuerda en N
• μ es la densidad lineal en kg/m

Ondas longitudinales en una barra elástica

Deformación del elemento

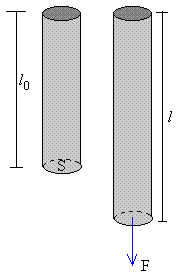
Existe una relación de proporcionalidad entre el esfuerzo (fuerza por unidad de área) y deformación unitaria (deformación por unidad de longitud).

${\displaystyle \frac{F}{S}=Y\frac{l-l_0}{l_0}}$

La constante de proporcionalidad Y se denomina módulo de Young y es característico de cada material

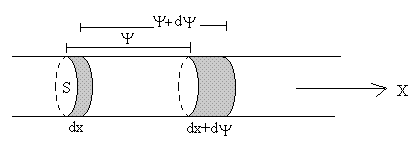
Consideremos un elemento de la barra de sección S en la posición x, que tiene una anchura dx. A causa de la perturbación, el elemento se desplaza Ψ y se deforma dΨ, de modo que la nueva anchura del elemento es dx+dΨ.

Calculamos la fuerza necesaria para producir esta deformación

${\displaystyle \frac{F}{S}=Y\frac{dx+d\Psi -dx}{dx}\frac{F}{S}=Y\frac{\partial \Psi }{\partial x}}$

A efectos de notación (derivada parcial) recuérdese que el desplazamiento Ψ, es una función de dos variables x (posición) y t (tiempo).

Desplazamiento del elemento

La parte izquierda de la barra ejerce una fuerza F sobre el elemento de barra de anchura dx, la parte derecha de la barra ejerce una fuerza F’ sobre dicho elemento

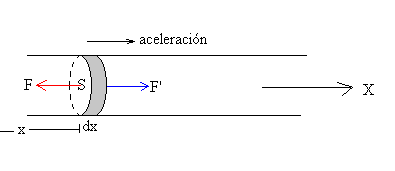
La fuerza neta es 

${\displaystyle F\text{'}-F=dF=SY\frac{{\partial }^2\Psi }{\partial x^2}dx}$

La segunda ley de Newton afirma que la fuerza sobre dicho elemento es igual al producto de la masa (densidad por volumen) por la aceleración (derivada segunda del desplazamiento)

${\displaystyle dF=\left(\rho Sdx\right)\frac{{\partial }^2\Psi }{\partial t^2}}$

Igualando ambas expresiones obtenemos la ecuación diferencial de un movimiento ondulatorio

${\displaystyle \frac{{\partial }^2\Psi }{\partial t^2}=\frac{Y}{\rho }\frac{{\partial }^2\Psi }{\partial x^2}}$

La fórmula de la velocidad de propagación es

${\displaystyle v=\sqrt{\frac{Y}{\rho }}}$

• Y es el módulo de la elasticidad del material o módulo de Young (expresado en N/m²)
• ρ es la densidad (expresada en kg/m³).

Fuente: Manual de Física, Koshkin N. I., Shirkévich M. G.. Editorial Mir (1975), pág. 106.

Referencias

Alonso M., Finn E. J. Física. Addison-Wesley Iberoamericana (1995), págs. 639-642