El sonido

Umbral de audición

El umbral de audición se define como la intensidad del sonido más bajo que el oído humano puede percibir y también, la intensidad del sonido más elevado que el oído humano puede tolerar.

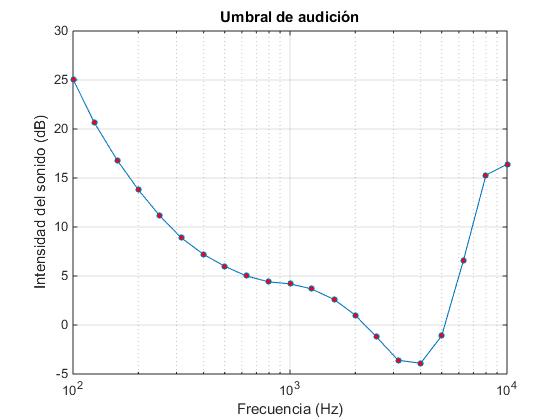
Se han tomado los datos de la tabla 1 (Minimum audible field thresholds) del documento titulado Hearing thresholds, para representarlos gráficamente en escala semilogarítmica. En el eje X, la frecuencia en Hz y en el eje Y, la intensidad del sonido en escala decibelios (dB).

f=[100,125,160,200,250,315,400,500,630,800,1000,1250,1600,2000...
,2500,3150,4000,5000,6300,8000,10000];
dB=[25.1,20.7,16.8,13.8,11.2,8.9,7.2,6.0,5.0,4.4,4.2,3.7,2.6,...
1.0,-1.2,-3.6,-3.9,-1.1,6.6,15.3,16.4];
semilogx(f,dB,'-o','markersize',4,'markerfacecolor','r')
xlabel('Frecuencia (Hz)')
ylabel('Intensidad del sonido (dB)')
title('Umbral de audición')
grid on

Analizamos el mínimo del umbral de audición, el intervalo de frecuencias entre 2000 y 5000 Hz. Añadimos el siguiente código al script anterior que realice las siguientes tareas

Que interpole mediante splines los datos comprendidos entre las frecuencias 2000 a 5000 Hz.
Que represente los datos y la interpolación en este intervalo de frecuencias
Que calcule la frecuencia para la cual se produce el mínimo

....
figure
fm=linspace(2000,5000);
dBm=interp1(f,dB,fm,'spline'); % interpolar cerca del mínimo
k=find(f>=2000 & f<=5000); 
hold on
semilogx(f(k),dB(k),'-o','markersize',4,'markerfacecolor','r') 
semilogx(fm,dBm,'r') 
hold off
legend('Lineal','spline',0)
xlabel('Frecuencia (Hz)')
ylabel('Intensidad del sonido (dB)')
title('Umbral de audición')
grid on

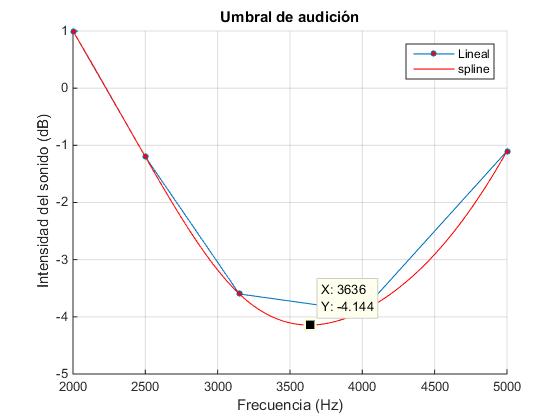
Se ha interpolado mediante spline los datos de la tabla (en color rojo) para obtener la frecuencia para la cual el umbral de acudicón presenta un mínimo.

>> [dBmin,kmin] = min(dBm)
dBmin =   -4.1444
kmin =    55
>> fm(kmin)
ans =  3.6364e+003

El mínimo se produce para la frecuencia 3636.4 Hz, valor que también podemos obtener en la ventana gráfica utilizando Data Cursor.

Medida de la intensidad del sonido

La intensidad del sonido se mide en W/m². Sin embargo a efectos prácticos el sonido se mide en la escala decibelios que se define del siguiente modo

$d B = 10 \cdot \log_{10} (\frac{I}{I_{0}}) I_{0} = 10^{- 12} \frac{W}{m^{2}}$

Para comprender la diferencia entre la escala física y la escala práctica se ha realizado el siguiente experiemento. Se coloca el sensor PASPORT Sound Level Sensor de PASCO. Este sensor mide el sonido en tres escalas siendo relevantes dos de ellas: decibelios y μW/m². Colocamos el sensor próximo a una fuente de sonido, en este caso un diapasón de 440 Hz. La intensidad del sonido producido al golpear el diapasón permenece al principio constante, después disminuye exponencialmente como podemos apreciar en la parte inferior de la gráfica (en color azul) que hemos obtenido con el programa DataStudio.

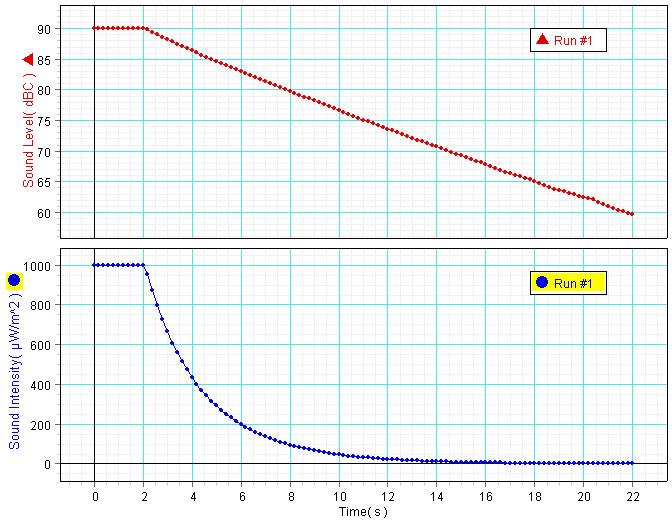
La escala decibelios es logarítmica, el logaritmo de la intensidad del sonido disminuye linealmente con el tiempo, tal como podemos apreciar en la gráfica superior de color rojo.

Comprobamos la correspondencia entre las dos escalas, por ejemplo a 1000 μW/m² le corresponde una medida de 90 dB.

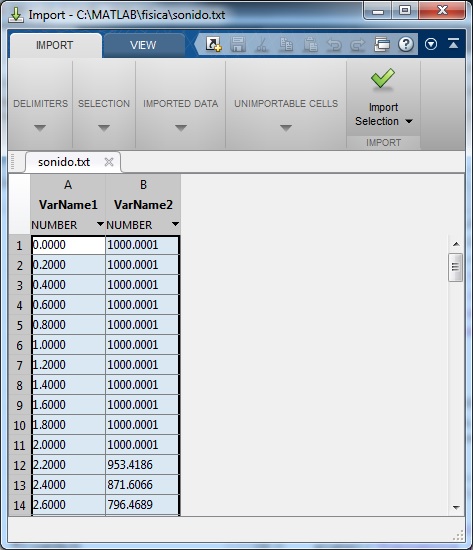
Exportamos los datos tomados por el sensor a un fichero de texto. Con el Bloc de Notas de Windows eliminamos la cabecera (dos líneas). Seleccionamos en el menú Edición/Reemplazar y sustituímos la coma (que separa la parte entera de los decimales) por un punto. Guardamos el fichero sonido.txt que se puede descargar en este enlace, lo colocamos en una carpeta accesible a MATLAB.

Seleccionamos en el menú de MATLAB, File/Import Data... e importamos el fichero sonido.txt con los datos. Apreciamos dos columnas en la primera el tiempo medido en segundos y en la segunda la intensidad del sonido medido en μW/m².

Elaboramos un script que realice las siguientes tareas:

Importar las dos columnas de datos con el comando load,
Extraer la primera columna de los datos de tiempo y guardarla en el vector tt.
Tomar del vector tt los datos de tiempo mayores o iguales que 2 segundos y establecer como origen de tiempo t=0 dicho instante creando un nuevo vector de tiempos t.
Extraer la segunda columna que corresponde a los datos de las intensidades y tomar solamente aquellas que correspondan a tiempos mayores o iguales que dos segundos.
Convertir la intensidad del sonido de μW/m² a decibelios
Representar gráficamente, el tiempo en el eje X y la intensidad medida en decibelios en el eje Y.
Ajustar los datos a una línea recta mediante la función MATLAB, polyfit o bien, de forma interactiva seleccionado en el menú de la ventana gráfica Tools/Basic Fitting, y activando la casilla linear
Representar dicha recta

load sonido.txt;
tt=sonido(:,1);
inten=sonido(:,2);
t=tt(tt>=2)-2;
dB=10*log10(inten(tt>=2)/1e-6);
hold on
plot(t,dB,'b')
p=polyfit(t,dB,1)
y=p(1)*t+p(2);
plot(t,y,'r')
hold off
grid on
legend('datos','ajuste lineal')
xlabel('Tiempo (s)')
ylabel('Intensidad (dB)')
title('Intensidad del sonido')

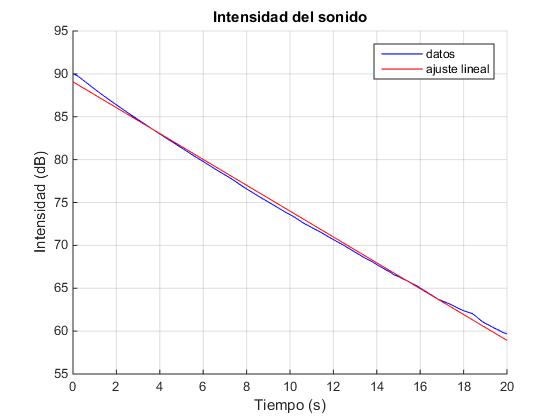
La intensidad del sonido decrece exponencialmente con el tiempo, de la forma I=I₀·exp(-γt). Tomando logaritmos decimales y multiplicando por 10.

$10 \cdot \log_{10} (\frac{I}{10^{- 12}}) = 10 \cdot \log_{10} (\frac{I_{0}}{10^{- 12}}) - (γ \cdot 10 \cdot \log_{10} e) t$

La pendiente de la recta es γ·10·log₁₀e, 1.5077, siendo γ la constante de amortiguamiento del sonido, como podemos ver en la ventana de comandos.

p =   -1.5077   89.0760

Análisis de Fourier del sonido del diapasón

El diapasón es un dispositivo metálico (generalmente de acero) en forma de horquilla utilizado principalmente como referencia para la afinación de instrumentos musicales.

En el laboratorio de Física de la Escuela de Ingeniería de Eibar, disponemos de un diapasón con caja de resonancia hecha de madera que viene marcado como 440 Hz. Colocamos un micrófono concectado a un ordenador, ponemos en marcha el programa Windows, Grabadora de sonidos situado Programas/Accesorios/Entretenimiento.

Golpeamos el diapasón con la varilla que acompaña al dispositivo y grabamos el sonido pulsando en el botón con el círculo de color rojo. Detenemos la grabación al cabo de 9.5 s, seleccionamos Archivo/Guardar como... para guardar el sonido en formato WAV en un fichero denominado diapason.wav que se puede descargar en este enlace. Durante la grabación no se ha podido evitar la inclusión de otros sonidos provenientes del exterior.

Situamos el fichero en una carpeta accesible a MATLAB. La función audioread carga el fichero diapason.wav y devuelve la amplitud de la señal en y, y la frecuencia de muestreo en Fs en Hz. Con estos datos representamos la señal en el tiempo.

[y,Fs] = audioread('diapason.wav');

%Representa la señal en el tiempo
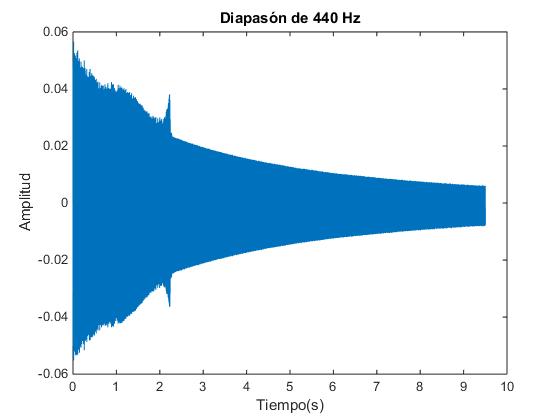
figure
N=length(y);
t=(1:N)/Fs;  %tiempo
plot(t,y)
xlabel('Tiempo(s)')
ylabel('Amplitud')
title('Diapasón de 440 Hz')

Añadimos al script las siguientes líneas para realizar la Transformada Rápida de Fourier, FFT y representar la señal en el dominio de frecuencias.

....
%representa la señal en frecuencia
figure
g=abs(fft(y));
g=g(1:N/2);      %Toma solamente N/2 datos
f=Fs*(0:N/2-1)/N;   %Frecuencias
plot(f,g)
xlim([0 1000])
xlabel('Frecuencia (Hz)')
ylabel('Amplitud')
title('Diapasón de 440 Hz')

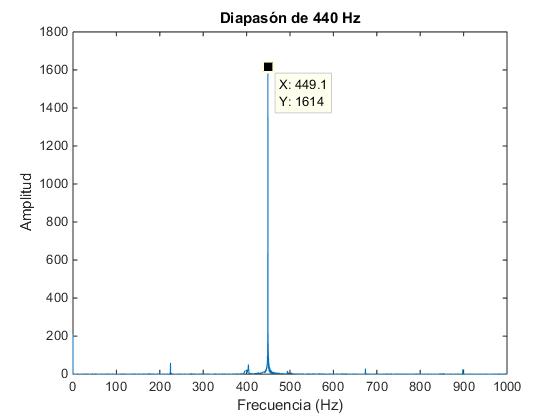
Con Data Cursor obtenemos la frecuencia del pico muy elevado, 449.1 Hz

Análisis espectral de instrumentos musicales

En esta sección, analizamos dos intrumentos musicales a partir de fragmentos de sonido grabados en ficheros .WAV que se pueden descargar desde la dirección https://drive.google.com/ open?id=1HL01sEdNAH9cTgWWcfkJrO_sWbB63lRU, véase el artículo de Oleksii Voronkin citado en las referencias

Saxofón

En primer lugar, descargamos el fichero 01_saxophone.wav. Creamos el script para representar la amplitud del sonido en función del tiempo

[y,Fs] = audioread('01_saxophone.wav');
N=length(y);
t=(1:N)/Fs;  %tiempo
plot(t,y)
xlabel('Tiempo(s)')
ylabel('Amplitud')
title('Saxofón')

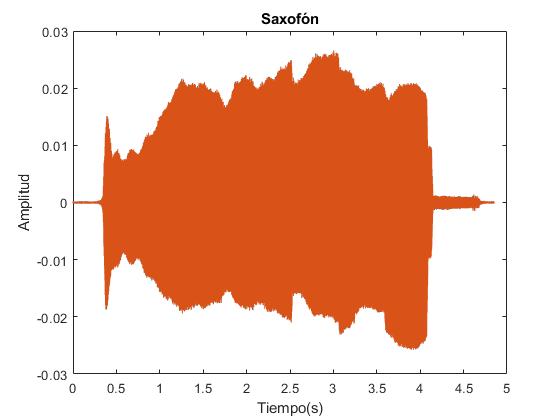
Ampliamos la representación gráfica con Zoom o representamos un pequeño fragmento de la señal acústica

[y,Fs] = audioread('01_saxophone.wav');
N=length(y);
t=(1:N)/Fs;  %tiempo
plot(t,y)
xlim([0.992,1.004])
grid on
xlabel('Tiempo(s)')
ylabel('Amplitud')
title('Saxofón')

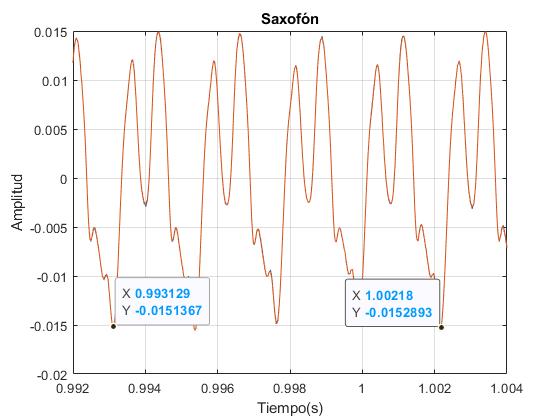
Con el cursor Data tip medimos la diferencia de tiempos X de cuatro oscilaciones completas, calculamos el periodo P=(1.00218-0.993129)/4=0.00226275 s y la frecuencia f=1/P=441.94 Hz

Realizamos la Transformada Rápida de Fourier, FFT y representamos la señal en el dominio de frecuencias.

[y,Fs] = audioread('01_saxophone.wav');
N=length(y);
g=abs(fft(y));
g=g(1:N/2);      %Toma solamente N/2 datos
f=Fs*(0:N/2-1)/N;   %Frecuencias
plot(f,g)
grid on
xlim([0 4000])
xlabel('Frecuencia (Hz)')
ylabel('Amplitud')
title('Saxofón')

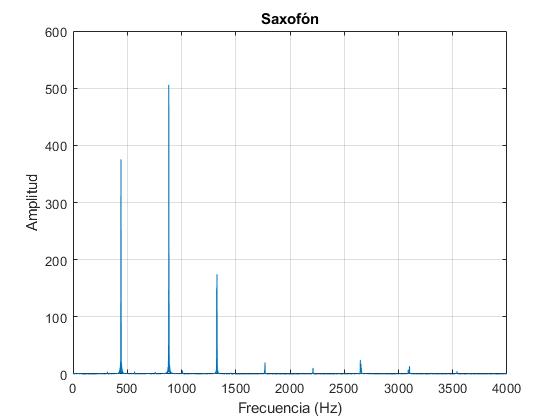
Con el cursor medimos las coordenadas X (frecuencia), Y (amplitud) de cada uno de los máximos. Los resultados son

Armónico	1	2	3	4	5	6	7
Frecuencia (Hz)	442	883	1327	1770	2212	2648	3101
Amplitud	375	506	174	16	11	25	13

Violín

En primer lugar, descargamos el fichero 02_violin.wav. Creamos el script para representar la amplitud del sonido en función del tiempo de un fragmento del fichero

[y,Fs] = audioread('02_violin.wav');
N=length(y);
t=(1:N)/Fs;  %tiempo
plot(t,y)
xlim([0.9890,0.9940])
grid on
xlabel('Tiempo(s)')
ylabel('Amplitud')
title('Violín')

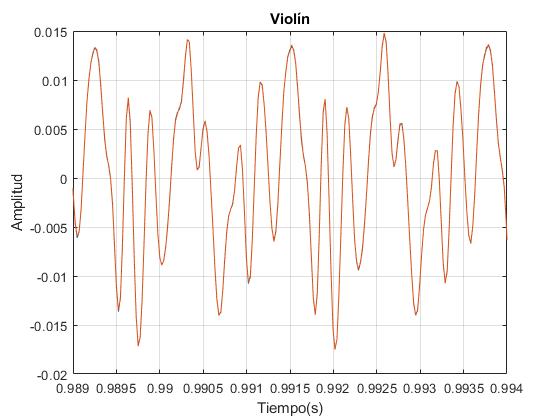
Realizamos la Transformada Rápida de Fourier, FFT y representamos la señal en el dominio de frecuencias.

[y,Fs] = audioread('02_violin.wav');
 N=length(y);
g=abs(fft(y));
g=g(1:N/2);      %Toma solamente N/2 datos
f=Fs*(0:N/2-1)/N;   %Frecuencias
plot(f,g)
grid on
xlim([0 4000])
xlabel('Frecuencia (Hz)')
ylabel('Amplitud')
title('Violín')

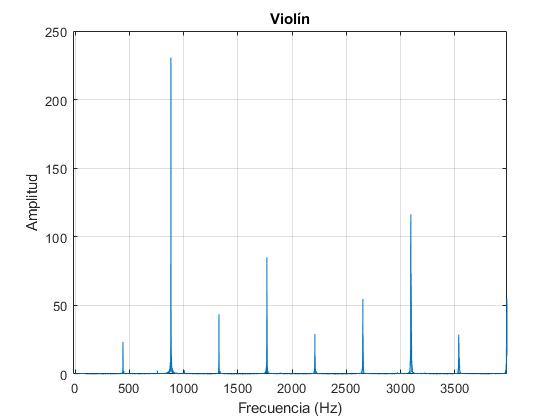
Con el cursor medimos las coordenadas X (frecuencia), Y (amplitud) de cada uno de los máximos. Los resultados son

Armónico	1	2	3	4	5	6	7	8
Frecuencia (Hz)	442	884	1326	1769	2211	2653	3095	3536
Amplitud	23	231	44	85	29	55	116	27

El lector interesado puede analizar otros instrumentos musicales descargando los ficheros .WAV correspondientes

Referencias

Oleksii Voronkin. Spectral Analysis of Musical Notes as a Source of Information About Musical Instruments. The Physics Teacher. Vol. 60, February 2022. pp. 117-122