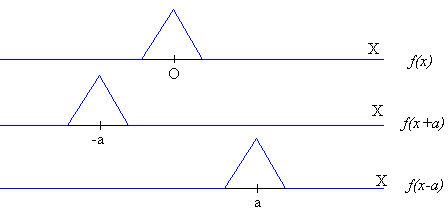
Consideremos una función Ψ=f(x), si reemplazamos x por x-a, obtenemos la función Ψ =f(x-a). La forma de la curva no cambia, los mismos valores se obtienen de Ψ para valores de x aumentados en a. Si a es una cantidad positiva, la curva se traslada sin cambiar de forma hacia la derecha desde el origen a la posición a. Del mismo modo Ψ=f(x+a) corresponde a un desplazamiento de la función hacia la izquierda, en la cantidad a.

Si a=vt, donde t es el tiempo, la función "se desplaza" con velocidad v.

Ecuación diferencial del movimiento ondulatorio

Cada vez que conozcamos que una propiedad física Ψ, por ejemplo el desplazamiento de un punto de una cuerda, satisface la ecuación diferencial

${\displaystyle \frac{{\partial }^2\Psi }{\partial t^2}=v^2\frac{{\partial }^2\Psi }{\partial x^2}}$

estamos describiendo un movimiento ondulatorio que se propaga a lo largo del eje X, con velocidad v.

Podemos comprobar que una solución de esta ecuación diferencial es Ψ=f(x-vt)

Clases de movimiento ondulatorios

El movimiento ondulatorio transversal es aquél en el que la dirección de propagación es perpendicular a la dirección de vibración, tal como sucede en una cuerda, o las ondas electromagnéticas.

En el movimiento ondulatorio longitudinal coinciden la dirección de vibración y de propagación, un ejemplo es el del sonido.

Actividades

Observamos la propagación de una perturbación en forma de un pulso triangular, sin distorsión, a lo largo del eje X, hacia la derecha. Dicha perturbación puede ser producida, por ejemplo, al dar un martillazo en el extremo de una barra de hierro.

En la parte inferior, vemos una imagen animada del movimiento de la fuente que produce el movimiento ondulatorio, situada en el origen. A la derecha, vemos el movimiento de las partículas del medio a medida que se propaga la perturbación. En particular, observamos el movimiento de las partículas situadas en la posición x=3.0 que tienen un color azul, diferente del resto, que son de color rojo.
Las partículas se mueven, pero retornan a sus posiciones de equilibrio cuando pasa la perturbación.

En el programa interactivo, observamos el movimiento de las partículas del medio y la representación gráfica en cada instante, de su desplazamiento Ψ (en el eje vertical) de la posición inicial de equilibrio (por razón de claridad, se ha exagerado este desplazamiento). Esta representación, se describe matemáticamente mediante la función Ψ =f(x-vt), tal como se ha justificado en el primer apartado.

Se introduce

• el valor de la velocidad de propagación v, en el control de edición titulado Velocidad

Se pulsa el botón titulado Nuevo.

Interferencia de dos pulsos

Una de las características esenciales del movimiento ondulatorio es el fenómeno de la interferencia.

En el programa interactivo, más abajo, se muestra la interferencia de dos pulsos iguales:

• uno que viaja de izquierda a derecha f(x-v·t)=exp(-(x+5-vt)²)

En el instante t=0, el máximo del pulso se encuentra en x=-5

• otro que viaja de derecha a izquierda f(x+v·t)=±exp(-(x-5+vt)²)

En el instante t=0, el máximo del pulso se encuentra en x=5

donde v es la velocidad de propagación que se ha fijado en v=1

Se activa uno de los dos botones de radio titulados:

• Pulsos del mismo sentido
• Pulsos de sentido opuesto

Se pulsa el botón titulado Nuevo

Se observa el movimiento de los dos pulsos (rojo y azul) en la parte superior y el resultado de la superposición en la parte inferior.

Un pulso se refleja en un extremo fijo

Consideremos un pulso que viaja de derecha a izquierda f(x+v·t)=exp(-(x-5+vt)²). En el instante t=0, el máximo del pulso se encuentra en x=5

El pulso se propaga hacia la izquierda y se refleja en el extremo fijo x=0. Solamente, hay movimiento ondulatorio en la región x≥0

Describimos este fenómeno como la superposición de dos movimientos ondulatorios, el incidente (en color rojo), y_i(x,t)=exp(-(x-5+vt)²) y el reflejado, (en color azul claro) que invertido se propaga de izquierda a derecha, y_r(x,t)=-exp(-(x+5-vt)²)

En la parte inferior, en color negro, se muestra el resultado de la superposición, el punto x=0, permanece fijo