Dinamika |
Partikula-multzoak Partikula-multzo baten dinamika Multzo isolatuak Blokea irristatzen aldapa mugikor batean Pendulua plataforma mugikor batean Partikula-bikotearen problema klasikoa Partikulak eta MZ nola mugitzen diren (I) Partikulak eta MZ nola mugitzen diren (II)
Kutxa bati tiraka |
Deskribapena | |||||||
| Irudiak erakusten du, salto batek denboran zehar dituen atalak: hasieran jauzilaria zutik dago, ondoren makurtu egiten da belaunak uzkurtuz, eta azkenik salto egiten du gora. Muskulu uzkurtuek duten energia potentzial elastikoa, lehenik energia zinetiko bilakatzen da, eta azkenik, jauzilaria punturik gorenera iristen denean, energia potentzial grabitatorio.
Orri honetan jauzilaria eredu sinple batez ordezkatuko da: partikula bi, m gainekoa eta M azpikoa, malguki elastiko batez lotuta (k konstanteduna) eta denak posizio bertikalean. Eredu hori partikula-multzoen dinamikaren ekuazioekin azter daiteke. Gogora ditzagun oinarrizko ideia bi: Partikula bakoitza mugitzen da kanpo indarren eraginpean (grabitatea, erreakzio normala...) eta barne indarren eraginpean (beste partikulak malgukiaren bitartez egiten dion bultzada). Masa-zentroa mugitzen da partikula bat bezala, multzo osoaren masarekin eta kanpo indarren erresultantearen eraginpean soilik.
DeskribapenaHasierako egoera.Malgukiaren luzera, deformaziorik gabe, l da. Bertikalki kokatzen dugunean, gaineko m partikularen pisuaren eraginez, malgukia uzkurtu egiten da.
Beraz, malgukiaren deformazioa, oreka posizioan, hau da: l-xo=mg/k. Ekuazio horretako xo goiko partikularen oreka-posizioa da, lurretik neurtuta. Demagun malgukia gehiago zapaltzen dugula (d) eta askatu. Goiko partikularen hasierako posizioa hau da: x=l-mg/k-d, eta hasierako abiadura: dx/dt=0. Energiak Har dezagun energia potentzial grabitatorioaren zero-maila lurrean bertan. Partikula-bikotearen hasierako energiak bi termino ditu:
Orduan, hona hemen partikula-bikotearen hasierako energia, E0
Malgukia, zapaldu ondoren, askatzen denean partikula biak mugitzen hasiko dira eta beraz bikotearen masa-zentroa ere bai. Mugimenduak atal ezberdin bi ditu: 1. Azpiko partikula, M, lurrarekin kontaktuan dagoen bitartea, beraz pausagunean. 2. Azpiko partikulak, M-k, lurrarekin kontaktua galtzen duenean. Higiduraren lehen atalaBikoteak jasaten dituen indar guztiak kanpo indarrak eta barne indarrak dira. Egin dezagun bereizketa:
Higiduraren lehen atalaren amaiera.Higiduraren lehen atala amaitzen da, azpiko partikulak (M masadunak) zorua ukitzeari uzten dionean, alegia N erreakzioa nulua denean. Hori gertatzen den aldiuneari to deitzen badiogu:
Baina kosinua ezin da unitatea baino handiagoa izan, beraz N=0 izan dadin honako baldintza bete behar da: (m+M)g≤kd Horrek esan nahi du, hasieran malgukiari ematen diogun d deformazio gehigarria oso txikia bada (muga bat baino txikiagoa), orduan ez da beteko aurreko baldintza hori, eta beraz ez du salto egingo. Azpiko partikula geldi geratuko da eta gainekoa Higidura Harmoniko Sinpleaz mugituko da, izan ere, d anplitudeaz. Bestalde, salto egiteko baldintza betetzen bada, t0 aldiunean:
Energiak Edozein partikula-multzotan: Wk=Uf -Ui Wk kanpo-indarren lana da, eta U multzoaren energia totala. U-k bakarrik hartzen ditu kontutan energia zinetikoak eta barne-indarren energia potentzialak. Kasu honetan kanpo indarrak bi dira: alde batetik, zoruaren erreakzio normala: N, ez du lanik egiten, mugitzen ari ez den partikula bati eragiten ari zaiolako. Bestetik, bi partikulen pisuak baina, kontserbakorra denez, berak egindako lana energia potentzialen aldakuntza da: Wk=Epi-Epf Hortaz, Ui+Epi=Uf+Epf=kte Partikula-multzo baten U energia da, partikulen energia zinetikoen batura eta euren arteko elkarrekintzaren energia potentziala. M masadun azpiko partikula pausagunean dago. Gaineko partikularen posizioa x da eta bere abiadura dx/dt. Malgukiaren deformazioa l-x da. Beraz partikula bikote horren energia kontserbatzen dela honela adieraz daiteke:
Lehen atala amaitzen denean, partikula-bikotearen energia E1 da, eta hiru termino ditu:
Zenbait ordezkapen eginez, egiaztatzen da lehen atalaren amaierako energia (E1) eta hasierako energia (E0) berdinak direla.
Bulkada eta momentu lineala
Higiduraren bigarren atala
Beraz, hona hemen higiduraren ekuazioak:
Hona hemen partikula bien arteko higidura erlatiboaren ekuazioa: Partikula bakoitzaren higidura ekuazioa Honezkero, ezagunak dira masa-zentroaren posizioa (z) eta partikulen arteko posizio erlatiboa (ξ=x-y) denboraren menpe. Ekuazio biko sistematik x eta y bakan daitezke: Bikotearen energiak bost termino ditu bigarren atalean, alegia t>t0 denean:
Zenbait ordezkapen eginez, egiaztatzen da bigarren atalaren energia (E2) eta hasierako energia (E0) berdinak direla.
SaiakuntzaAukeran idatz daitezke:
Berria botoia sakatu. Malgukia bere oreka posizioraino uzkurtzen da, gaineko partikularen pisuaren eraginez, baina ez da mugitzen. Mugitzen hasteko, malgukia are gehiago zapaldu behar da, d distantzia, gaineko partikulari (gorriari) saguaz eragiten. Hasi botoia sakatu.
Partikula bikotea (gorria eta urdina) eta malgukia mugitzen hasten dira. Bikotearen masa-zentroa beltzez adierazten da. Higiduraren atal biak erraz bereiz daitezke:
Adibidea:
Berria botoia sakatu. Gaineko partikularen pisuak malgukia zapaltzen du: mg/k=0.052 m. Beraz partikularen oreka-posizioa, x=l-mg/k=0.45 m. Horretaz gain, konprima bedi malgukia d=0.2 m gehiago, alegia, gaineko partikularen posizioa honakoa izan arte: x=0.25 m. Hasi botoia sakatu. Lehen ataleko oszilazioaren maiztasun angeluarra, ω1 :
Azpiko partikulak jasaten duen N erantzun normala gutxitzen doa eta, halako batean, kontaktua galtzen du. Hori gertatzen den aldiunea: t0 da.
Aldiune horretan MZ-aren posizioa:
Eta MZ-aren abiadura une horretan:
Ondoren, masa zentroak altuera maximoa atzematen du bere abiadura anulatzera iristen denean: v=0 0=v0 -g·(t-t0) Hori gertatzen den aldiunea: t=0.23+0.12=0.35 s. Eta masa-zentroak atzematen duen altuera maximoa: z=z0+v0(t-t0)-g(t-t0)2/2 z=0.66 m Bigarren ataleko maiztasun angeluarra: ω2.
Partikulen posizio erlatiboa honela kalkulatzen da: ξ=x-y
Eta honezkero, MZ-aren posizioa ezagututa (z) eta partikulen posizio erlatiboa (ξ), orduan partikula bakoitzaren posizioa ere kalkula daiteke: 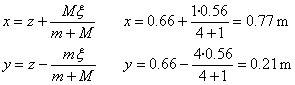 |
"Berria" botoia sakatu, gaineko partikula (gorria) beherago jaitsi eta azkenik "Hasi" botoia sakatu.
Dufresne R., Gerace W., Leonard W. Springbok: The Physics of jumping. The Physics Teacher Vol 39, February 2001, pp. 109-115