Se estudia el proceso de evaporación suponiendo que las pérdidas de calor son importantes y obedecen a la ley de enfriamiento de Newton

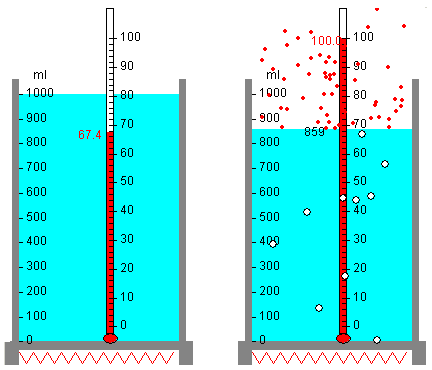
Se coloca un recipiente con una masa m de agua sobre un hornillo eléctrico de potencia P.

La temperatura inicial del agua es T_a, la temperatura ambiente. A medida que transcurre el tiempo, se va elevando la temperatura del agua, hasta que entra en ebullición a 100 ºC en el instante t₁.

P·t₁=m·c·(100-T_a)
El agua se evapora, disminuyendo el nivel de agua en el recipiente  en el instante t se habrá evaporado una masa m_e de agua

P·(t-t₁)=m_e·L_v

donde L_v es el calor de evaporación del agua

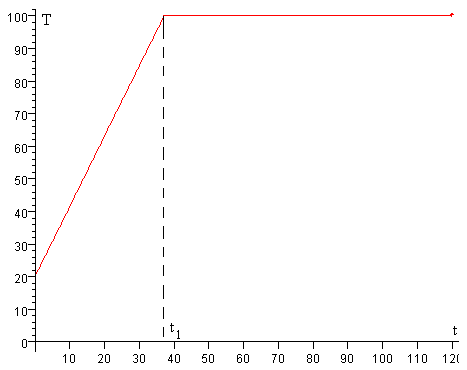
Con pérdidas

Ahora bien, las pérdidas de calor son importantes  ya que la diferencias de temperatura entre el agua en ebullición y el ambiente es muy grande. Vamos a formular de nuevo, el problema teniendo en cuenta las pérdidas de calor y supondremos que obedecen a la ley de enfriamiento de Newton.

El calor dQ=P·dt suministrado por el hornillo eléctrico en el intervalo de tiempo entre t y t+dt se invierte:

• En elevar la temperatura del agua mc·dT

• Se transfiere a la atmósfera αS (T-T_a)·dt de acuerdo con la ley del enfriamiento de Newton. Donde α es el coeficiente de intercambio de calor y S es el área del cuerpo en contacto con la atmósfera. T es la temperatura del agua y T_a es la temperatura ambiente

${\displaystyle \begin{array}{l}P=\frac{dQ}{dt}=mc\frac{dT}{dt}+\alpha S(T-T_a)\\ \frac{dT}{dt}=\frac{P}{mc}-\frac{\alpha S}{mc}(T-T_a)\end{array}}$

Integramos la ecuación diferencial con las siguientes condiciones iniciales, en el instante t=0, la temperatura del agua es la temperatura ambiente T_a.

${\displaystyle \begin{array}{l}{\displaystyle \underset{T_a}{\overset{T}{\int }}\frac{dT}{\frac{P}{mc}-\frac{\alpha S}{mc}(T-T_a)}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ -\frac{mc}{\alpha S}\ln \left(\frac{P}{mc}-\frac{\alpha S}{mc}(T-T_a)\right)+\frac{mc}{\alpha S}\ln \left(\frac{P}{mc}\right)=t\end{array}}$

Despejamos la temperatura T del agua

${\displaystyle \begin{array}{l}T=T_a+\frac{P}{\alpha S}\left(1-\exp \left(-\frac{\alpha S}{mc}t\right)\right)\\ T=T_a+\frac{P}{\alpha S}\left(1-\exp \left(-t/\tau \right)\right)\tau =\frac{mc}{\alpha S}\end{array}}$

τ se denomina constante de tiempo.

La temperatura T crece hasta que alcanza un límite cuando t→∞

${\displaystyle T_{\infty }=T_a+\frac{P}{\alpha S}}$

Puede ocurrir dos casos:

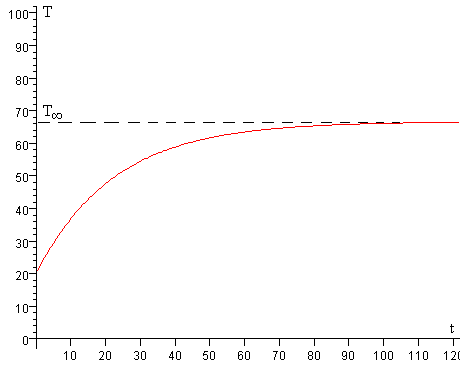
1. Que las pérdidas αS sean grandes o la potencia P del hornillo sea pequeña de modo que T_∞<100, entonces la temperatura del agua crece desde T_a hasta T_∞ pero el agua no entra en ebullición.



2. Que las pérdidas αS sean pequeñas o la potencia P del hornillo sea suficiente de modo que T_∞>=100, entonces la temperatura del agua crece desde T_a hasta 100ºC, el agua entra en ebullición y luego, se va evaporando hasta que se agota

Poniendo T=100 y despejamos el instante t₁ en el que el agua entra en ebullición

${\displaystyle t_1=-\frac{mc}{\alpha S}\ln \left(1-\frac{\alpha S}{P}(100-T_a)\right)}$

Cuando las pérdidas son pequeñas αS→0, utilizamos la aproximación ln(1+x)≈x

${\displaystyle t_1=\frac{mc(100-T_a)}{P}}$

Que es el resultado que obtuvimos suponiendo que no hay pérdidas

A partir de este momento, la temperatura del agua se mantiene constante. El calor dQ=P·dt suministrado por el hornillo eléctrico en el intervalo de tiempo entre t y t+dt se invierte:

• en evaporar una masa dm de agua, L_v·dm, siendo L_v es el calor de evaporación del agua

• se transfiere a la atmósfera αS (100-T_a)·dt, ley del enfriamiento de Newton.

P·dt=L_v·dm+αS (100-T_a)

La masa m_e de agua evaporada en el instante t>t₁ es

${\displaystyle m_e=\frac{1}{L_v}(P-\alpha S(100-T_a))(t-t_1)}$

El agua que permanece líquida en el recipiente es m-m_e

Si no hubiese pérdidas, αS=0

${\displaystyle m_e=\frac{P(t-t_1)}{L_v}}$

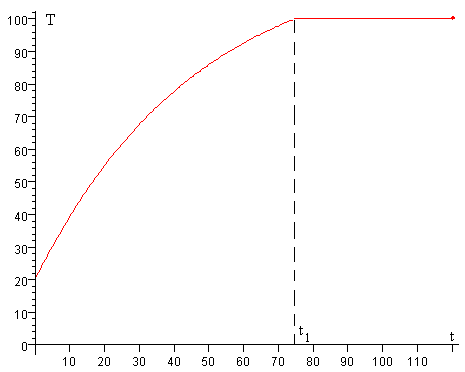
Ejemplo:

• La masa de agua en el recipiente, m=1.0 kg de agua

• La potencia del hornillo, P=150 W

• La temperatura ambiente T_a=20ºC

• El calor específico del agua es c=4180 J/(kg ºC)

• El calor de evaporación del agua es L_v=2260·10³ J/kg

• El coeficiente de las pérdidas de calor αS=1.5 J/ºC

1. Con pérdidas

La temperatura T crece

${\displaystyle T_{\infty }=T_a+\frac{P}{\alpha S}{T}_{\infty }=20+\frac{150}{1.5}=120\text{ºC}}$

Como T_∞>100, la temperatura T del agua crece hasta alcanzar la temperatura de ebullición T=100ºC en el instante t₁

${\displaystyle \begin{array}{l}{t}_1=-\frac{mc}{\alpha S}\ln \left(1-\frac{\alpha S}{P}\left(100-T_a\right)\right)\\ t_1=-\frac{1.0·4180}{1.5}\ln \left(1-\frac{1.5}{150}\left(100-20\right)\right)=4485\text{s}=74.7\text{min}\end{array}}$

A partir del instante t>t₁ el agua se evapora.

En el instante t=120 min=7200 s se ha evaporado

${\displaystyle \begin{array}{l}{m}_e=\frac{1}{L_v}(P-\alpha S(100-T_a))(t-t_1)\\ m_e=\frac{1}{2260·{10}^3}(150-1.5(100-20))(7200-4485)=0.036\text{kg }\end{array}}$

Se han evaporado 36 ml de agua y permanecen 1000-36=964 ml en estado líquido

2. Sin pérdidas αS=0.

${\displaystyle t_1=\frac{mc(100-T_a)}{P}{t}_1=\frac{1.0·4180·(100-20)}{150}=2229\text{s}=\text{37}\text{.1}\text{min}}$

A partir del instante t>t₁ el agua se evapora.

En el instante t=120 min=7200 s se ha evaporado

${\displaystyle m_e=\frac{P(t-t_1)}{L_v}{m}_e=\frac{150·(7200-2229)}{2260·{10}^3}=0.330\text{kg}}$

Se han evaporado 330 ml de agua y permanecen 1000-330=670 ml en estado líquido

3. La potencia del hornillo eléctrico se reduce a P=75 W

La temperatura T crece

${\displaystyle T_{\infty }=T_a+\frac{P}{\alpha S}{T}_{\infty }=20+\frac{75}{1.5}=70\text{ºC}}$

Como T_∞<100, la temperatura T del agua no alcanza la temperatura de ebullición

Ta=20; %temperatura inicial de la placa y ambiente
P=150; %potencia del hornillo
c=4180; %calor específico del agua
Lv=2260000; %calor latente de ebullición del agua
m=1; %masa
aS=1.5; %coef. pérdidas de calor

%temperatura final
Tf=Ta+P/aS;
if Tf>=100
    tf=-m*c*log(1-aS*(100-Ta)/P)/aS %instante que alcanza 100 ??C
    fprintf('Comienza la ebullición: %3.1f min\n',tf/60);
    t1=0:20:tf;
    T1=Ta+P*(1-exp(-aS*t1/(m*c)))/aS;
    t2=tf:20:60*120;  %hasta 120 minutos
    T2=ones(1,length(t2))*100;
    t=[t1 t2];
    T=[T1 T2];
else
    t=0:20:60*120; %hasta 120 minutos
    T=Ta+P*(1-exp(-aS*t/(m*c)))/aS;
    fprintf('Temperatura final: %2.1f °C\n',Ta+P/aS);
end
plot(t,T,'b')
ylim([0 105])
xlim([0 t(end)])
grid on
xlabel('t (s)')
ylabel('T (°C)')
title('Ley del enfriamiento de Newton')

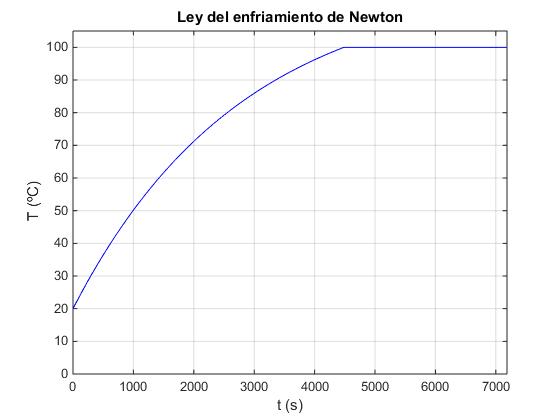
Comienza la ebullición: 74.7 min

Modificamos la potencia del hornillo

Ta=20; %temperatura inicial de la placa y ambiente
P=75; %potencia del hornillo
...

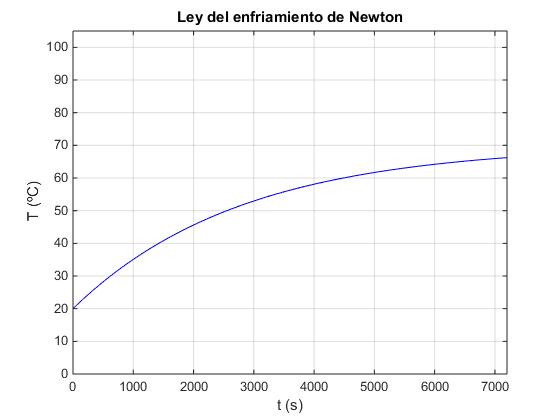
Temperatura final: 70.0 °C

Actividades

Se ha fijado

• La masa de agua en el recipiente, m=1.0 kg de agua

• La temperatura ambiente T_a=20ºC

• La temperatura inicial del agua en el recipiente T=20ºC

Se introduce

• La potencia eléctrica del hornillo P, en el control titulado Potencia

• El coeficiente de proporcionalidad αS en la ley del enfriamiento de Newton, en el control titulado Pérdidas

Se pulsa el botón titulado Nuevo

Se observa el incremento de la temperatura del agua que contiene el recipiente. Si la potencia del hornillo eléctrico es suficiente o las pérdidas no son grandes el agua alcanzará la temperatura de ebullición. Observaremos que el agua se evapora disminuyendo el agua líquida contenida en el recipiente sin cambiar la temperatura.

En el caso de que la potencia del hornillo eléctrico no sea suficiente o las pérdidas sean grandes, el agua  no alcanzará la temperatura máxima de ebullición.

En la parte derecha, se representa:

• En el eje horizontal, el tiempo en minutos
• En el eje vertical, la temperatura T del agua contenida en el recipiente.

Referencias

O'Connell J. Heating water: Rate correction due to Newtonian cooling. The Physics Teacher Vol 37, December 1999, pp. 551-552